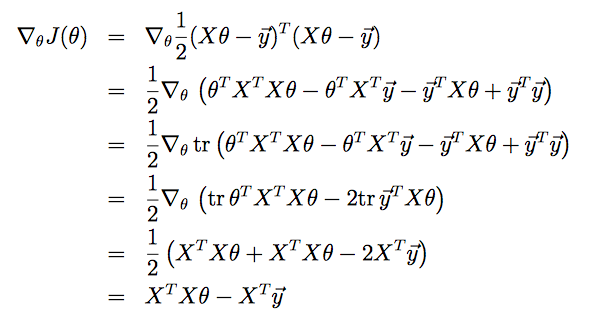机器学习三要素
机器学习的三要素为:模型、策略、算法。
策略:按照什么样的准则学习或选择最优的模型。
最小化均方误差,即所谓的 least-squares(在spss里线性回归对应的模块就叫OLS即Ordinary Least Squares):
算法:基于训练数据集,根据学习策略,选择最优模型的计算方法。
确定模型中每个θi取值的计算方法,往往归结为最优化问题。对于线性回归,我们知道它是有解析解的,即正规方程 The normal equations:![]()
监督学习(Supervised Learning)
SupervisedLearning,Wiki
通过训练资料(包含输入和预期输出的数据集)去学习或者建立一个函数模型,并依此模型推测新的实例。函数的输出可以是一个连续的值(回归问题,Regression),或是预测一个分类标签(分类问题,Classification)。
机器学习中与之对应还有:
无监督学习(Unsupervised Learning)
强化学习(Reinforcement Learning)

在课程中定义了一些符号:
x(i):输入特征(input features)
y(i) :目标变量(target variable)
(x(i),y(i)) :训练样本(training example)
{(x(i),y(i));i=1,...,m} :训练集合(training set)
m :训练样本数量
h :假设函数(hypothesis)
线性回归(Linear Regression)
例子:房屋价格与居住面积和卧室数量的关系
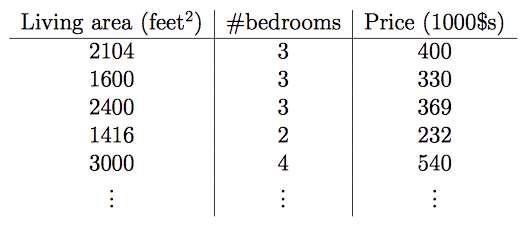
在这里输入特征变成了两个x1,x2,目标变量就是价格
x1: Living area
x2: bedrooms
可以把它们称之为x的二维向量。
在实际情况中,我们需要根据你所选择的特征来进行一个项目的设计。
我们之前已经了解了监督学习,所以需要我们决定我们应该使用什么样的假设函数来进行训练参数。线性函数是最初级,最简单的选择。
所以针对例子假设函数:
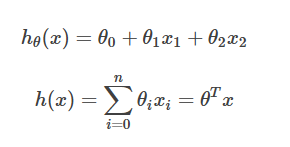
其中的θ就是要训练的参数(也被成为权重),我们想要得到尽可能符合变化规律的参数,使得这个函数可以用来估计价格。
因为要训练θ,所以引入cost function(损失函数/成本函数)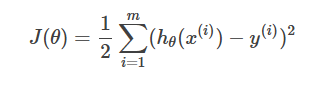
对于线性规划问题,通常J函数(误差平方和)是碗状的,所以往往只会有一个全局最优解,不用过多担心算法收敛到局部最优解。
最小二乘法(LMS algorithm)
课程中的比喻很形象,将用最快的速度最小化损失函数 比作如何最快地下山。也就是每一步都应该往坡度最陡的方向往下走,而坡度最陡的方向就是损失函数相应的偏导数,因此算法迭代的规则是:

其中α是算法的参数learning rate,α越大每一步下降的幅度越大速度也会越快,但过大有可能导致算法无法收敛。
假设只有一个训练样本:(x,
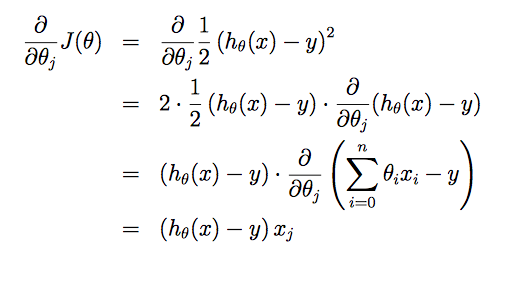
更新函数为:θj:=θj+α(y
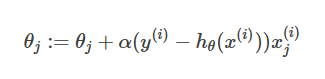
这就是最小二乘法(LMS, least mean squares)更新规则。
梯度下降(gradient descent)
在面对多个样本进行处理时,就需要在此基础上演变更新规则。有两种策略:
批量梯度下降 batch gradient descent 
随机梯度下降 stochastic gradient descent (incremental gradient descent) 
当训练样本量很大时,batch gradient descent的每一步都要遍历整个训练集,开销极大;而stochastic gradient descent则只选取其中的一个样本。因此训练集很大时,后者的速度要快于前者。
虽然 stochastic gradient descent 可能最终不会收敛到最优解(代价函数等于0),大多数情况下都能得到真实最小值的一个足够好的近似。
正规方程组(normal equations)
梯度的矩阵表示

针对矩阵中的每个元素对 f 求导,将导数写在各个元素对应的位置。
矩阵的迹
一个 n×n 矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。
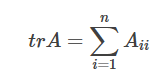

对Normal Equation求解

对J式子进行展开化简
推倒过程利用了矩阵的迹的性质。因为J(θ)是个实数,所以它的迹等于它本身。

线性回归代价函数的选择
为什么在选择策略J(θ)时,使用误差h(x)-y的平方和。而不是其他代价函数?
线性回归的模型及假设:![]()
ε(i) ∼ N(0, σ2),随机误差ε服从正态分布(Gaussian分布)
ε(i) 是 IID的,即独立同分布的
于是可以获得目标变量的条件概率分布:
整个训练集的似然函数,与对数似然函数分别为:
因此,最大化对数似然函数,也就相当于最小化
局部加权线性回归 (Locally weighted linear regression,LWR)
在线性回归中,使用某个训练样本 x 通过评价h(x)来更新 θ 时,其余样本对更新的贡献是相同的;
在LWR中,使用某个训练样本 x 通过评价h(x)来更新 θ 时,离 x 近的点的重要性更高。
加权函数w的一个选择是指数衰减函数,是一个钟形 bell-shaped曲线,虽然长得像高斯分布,但它不是高斯分布:
|x(i) − x| 越小,距离越近,其权重w(i)越接近1; |x(i) − x|越大,则权重w(i)越小。
τ 被称为bandwidth带宽参数,控制 x(i) 的权重值随着离 x 距离大小而下降的速率。τ越大,下降速度越慢
在调整 θ 的过程中。如果x(i) 权重大,要努力进行拟合 使误差平方项最小。如果权重很小,误差平方项将被忽略。
对新的 x 进行预测时,LWR和线性回归也有区别:
- LWR是一个非参数算法 non-parametric algorithm:对每个新的 x 进行预测时,都需要利用训练集重新做拟合,代价很高(因此有课上的学生质疑这是否称得上是一个模型)。
- 线性回归是一个参数算法:参数个数是有限的,拟合完参数后就可以不考虑训练集,直接进行预测。
likelihood 和 probability的区别
probability 强调 y 发生的概率
likelihood 强调给定一组x,y。找到 θ 使 x 条件下 y 发生的几率最大。
参考:
https://blog.csdn.net/TRillionZxY1/article/details/76290919
https://www.cnblogs.com/logosxxw/p/4651231.html