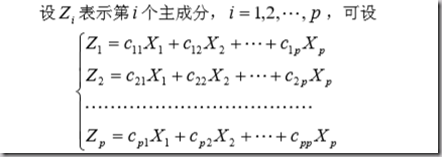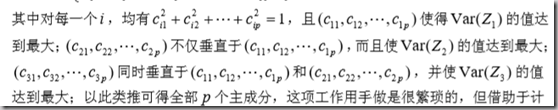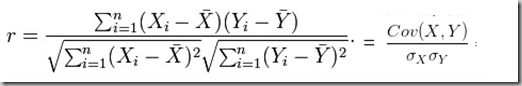【数学建模】day10-主成分分析

主成分分析是一种常用手段。这应该与因子分析等区别开来，重点在于理解主成分分析的作用以及什么情况下使用主成分分析。

主成分分析是一种降维方法。

例如我们要做回归分析，如果自变量众多，彼此之间又具有复杂的相关性，那么我们考虑对自变量个数进行“减少”。而这个减少不能够丢失有效信息，由此可以使用主成分分析。

主成分分析的主要思想是，对原始众多自变量进行【线性组合】，从而得到新的变量(个数通常比原始变量少)。对于每一个新变量，其线性组合的系数向量叫该主成分的方向；不同主成分的方向是正交的，从而保证新的变量彼此不相关，消除了糅合性。

具体来说，是：

原始变量Xi(i = 1,2,…p)，主成分变量Z(z = 1,2…p)，则：

其中，要求满足：

注意：

　　1）主成分分析的结果受量纲的影响，由于各变量的单位可能不一样，如果各自改 变量纲，结果会不一样，这是主成分分析的大问题，回归分析是不存在这种情况的， 所以实际中可以先把各变量的数据标准化，然后使用协方差矩阵或相关系数矩阵进行分析。 

　　2）使方差达到大的主成分分析不用转轴（由于统计软件常把主成分分析和因子 分析放在一起，后者往往需要转轴，使用时应注意）。 

　　3）主成分的保留。用相关系数矩阵求主成分时，Kaiser主张将特征值小于1的主成 分予以放弃（这也是SPSS软件的默认值）。 

　　4）在实际研究中，由于主成分的目的是为了降维，减少变量的个数，故一般选取 少量的主成分（不超过5或6个），只要它们能解释变异的70％～80％（称累积贡献率） 就行了。 

如何选取主成分？

明确目的在于线性组合原始变量得到：

（z是向量）

在系数平方和为1下，使得z的方差最大。（这样就使得新的变量z1，z2…差异最大，就代表我们抓住了原始变量的大多数信息）；同时，保证各个主成分变量的系数矩阵c两两正交（这代表我们使得新的变量彼此不糅合，不相关）。

设原始变量数据：

（X称作设计阵）

首先将X标准化。

设新变量z = c1x1 + c2x2 +… + cpxp；

系数向量C = (c1,c2,…cp).T

由于使得方差最大，无偏样本方差为：

M = (∑(z(i) - z均)^2) / (n-1） = （XC).T *(XC) / (n-1)

该方差M在||C|| = 1的条件下取得最大值，是在下列计算下取到的：

M取最大值的系数矩阵C，（设计阵是X），就是X.T * X的最大特征值对应的标准正交特征向量。 【也就是：矩阵(X.T * X) / (n-1)的特征向量；这个矩阵就是相关系数矩阵！】

从而，只需计算X.T*X 的特征值以及对应的特征向量，从而特征向量就是主成分变量表达式的系数。

再求第个主成分变量，只需要再利用第二大的特征值以及特征向量。

这里，X标准化后，X.T*X / (n-1)实际上是原始变量x1,x2…xp的相关系数矩阵。

求解时，实际上是计算这个相关系数矩阵。

PCA步骤：

　　1. 列出设计阵X

　　2. 求相关系数矩阵 R =（X.T * X）/ ( n-1) 的特征值（从大到小排列），以及对应的标准正交特征向量。

　　3. 从特征值大到小选择PCA变量：先选取最大的特征值以及其特征向量，从而构成第一个主成分变量。计算累计贡献率：已选取的特征值之和占所有特征值之和的比重。

　　4. 重复步骤3，直到累计贡献率达标或者选取了足够的PCA变量。

　　5. 单纯考虑累积贡献率有时是不够的，还需要考虑选择的主成分对原始变量的贡献 值，我们用相关系数的平方和来表示.如果选取的主成分为 z1,z2,…zr ，则它们对原 变量 xi 的贡献值为:

　　　　　　　　　　pi = ∑ (r(zj,xi))^2；

　　　　　（即每一个主成分变量与xi的相关系数平方的和。）

　　6. 进而我们可以用主成分变量对问题做出其他分析（如回归分析等）。

注：两个向量的相关系数就是两向量夹角的余弦，展开来说就是：

例子：

MATLAB做主成分分析，函数用法、例子以及代码实现，后补。