一、主成分分析

维度是数据科学中的一个关键属性，维度是数据集的所有特征。例如，如果您正在查看包含音乐片段的数据集，维度可能是流派、片段的长度、乐器的数量、歌手的存在等等。

您可以将所有这些维度想象为不同的列。当只有两个维度时，可以使用X和Y轴绘制它。如果添加颜色，您可以表示第三个维度。如果你有几十个或几百个维度，它也是类似的，只是更难具象化它。

当你有这么多维度时，其中一些是相关的。例如，我们可以想当然地认为一段音乐的流派将与该作品中出现的乐器相关。降低维度的一种方法是只保留其中的一些维度。但很有可能丢失了代表性强的信息。所以需要一种方法可以减少这些维度，同时保持数据集中存在重要信息。

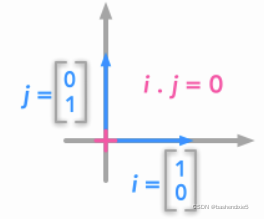
主成分分析(PCA) 的目的是减少数据集的维数。PCA为我们提供了一组新的维度，即主成分(PC)。它们是有序的：第一个主成分是与最大方差相关的维度。此外，主成分是正交的。请记住，正交向量意味着它们的点积等于0。这意味着每个主成分都与前一个主成分不相关。您可以选择只保留前几个主成分，因为每个主成分都是数据特征的线性组合。例如，一个主成分可以是乐曲长度和演奏乐器数量的线性组合。

单位向量是正交向量的一个例子。

二、数学推导

1、问题描述

该问题可以表示为找到一个函数，该函数的作用是将一组数据点从，我们想改变数据集的维数n到l。如果l < n，新数据集将被压缩，因为它的特征数量减少了。我们还需要一个可以将转换后的数据集解码回初始数据集的函数：

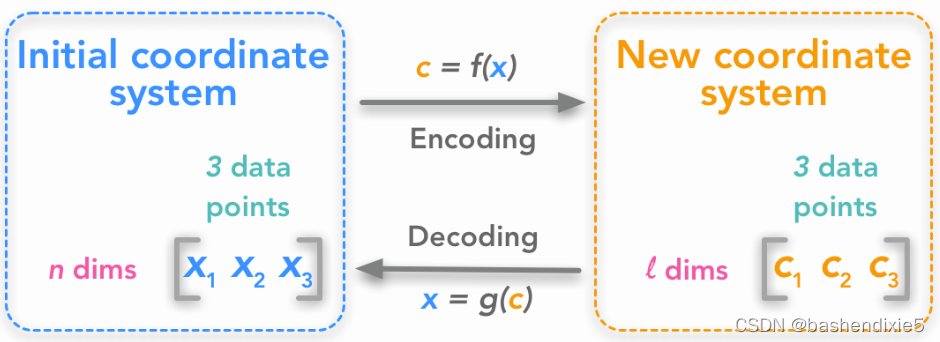
第一步是了解数据的形状。 x(i) 是一个包含 n 维的数据点。共有m个数据点：

体现n个维度的化，变为如下矩阵形式：

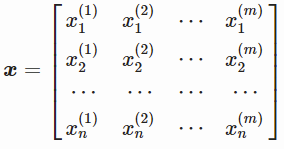也可以写成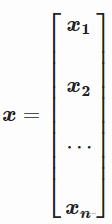

其中 x1⋯xn 是包含每个 m 个观测值的向量。

然后，我们的目标是将x转换为

2、约束条件

编码函数 f(x) 将 x 转换为 c，解码函数将 c 转换回 x 的近似值。为简单起见，PCA将遵守一些约束：

约束1：

解码函数必须是一个简单的矩阵乘法：g(c)=Dc；通过将矩阵 D 应用到来自新坐标系的数据集，应该变换回初始坐标系。

约束2：

D 的列必须是正交的。

约束3：

D 的列必须有单位范数。

3、寻找编码函数

暂时我们将只考虑一个数据点。因此，这些矩阵将具有以下维度：

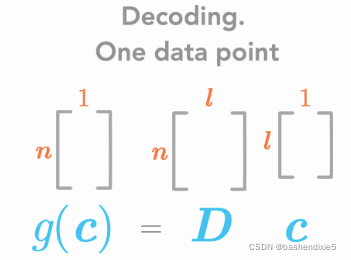
我们想要一个解码函数，它是一个简单的矩阵乘法。因此，我们有 g(c)=Dc。然后我们将从解码函数中找到编码函数。

我们希望最小化解码数据点和实际数据点之间的误差。这意味着要减少 x 和 g(c) 之间的距离。我们将使用平方 L2 范数作为误差指标。

让我们称 c*为最优c，

这意味着我们想要找到向量 c 的值，使得尽可能小。

向量 y 的平方 L2 范数可以表示为：

我们将变量命名为 y 以避免与 x 混淆。这里 y=x−g(c)。

因此，我们想要最小化的方程变为：

可得

通过分配性质可得

通过变换性质可知

由于的结果是一个标量，所以

所以方程变为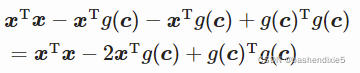

第一项不依赖于 c，因为我们想根据 c 最小化函数，所以我们可以去掉这个项。我们简化为：

由于 g(c)=Dc：

由于

故

正如我们已知的，因为 D 是正交的（实际上，如果 n≠l，它是半正交的）并且具有单位范数列。我们可以在等式中替换：

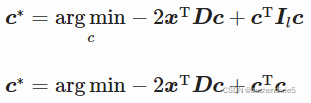
4、最小化函数

现在的目标是找到函数的最小值。一种广泛使用的方法是使用梯度下降算法。这不是我们的重点，我们简单说一下，主要思想是函数在特定 x 值处的值导数告诉您是否需要增加或减少 x 以达到最小值。当斜率接近 0 时，应该已经达到最小值。

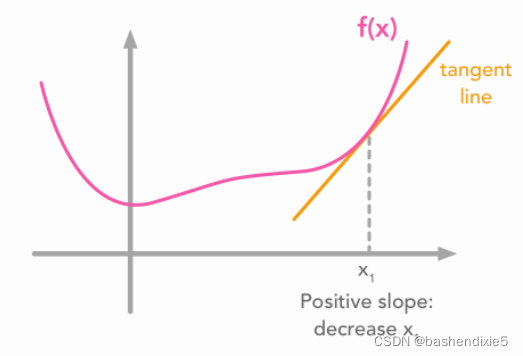
但是，具有局部最小值的函数可能会影响下降：

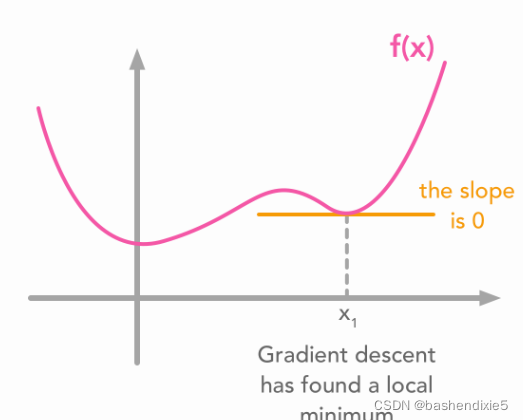
这些示例是二维的，但原理对于更高维的也是通用的。梯度是一个包含所有维度的偏导数的向量。它的数学符号是。

5、计算函数的梯度

在这里，我们希望通过 c 的每个维度最小化。我们正在寻找 0 的斜率。等式是：

让我们分别对两个项来计算导数。

第二项是

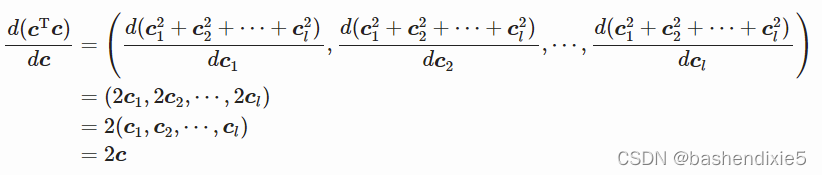
然后可得

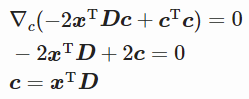
我们希望 c 是形状为 (l, 1) 的列向量，所以我们需要转置。

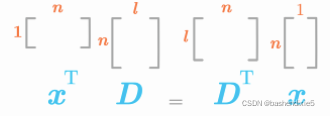
由于故

我们找到了编码函数

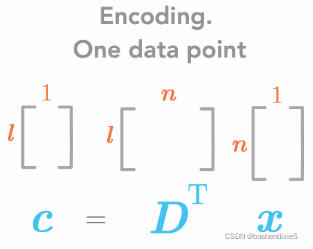
要从c回到x，使用g(c)=Dc。r(x) = g(f(x)) =

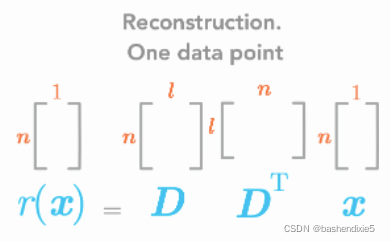
6、计算D

下一步是找到矩阵 D。PCA 的目的是改变坐标系，以便沿着投影空间的第一维最大化方差。这相当于最小化数据点及其重建之间的误差。请参阅下面的协方差矩阵以获取更多详细信息。

由于我们必须考虑所有点（所有点都将使用相同的矩阵 D），我们将使用误差的 Frobenius 范数，这相当于矩阵的 L2 范数。下面是 Frobenius 范数的公式：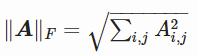

我们将 D∗ 称为最优 D（在误差尽可能小的意义上）。

我们有：

使用的约束，因为我们选择了使 D 的列正交的约束。

7、第一个主成分

我们暂时只找到第一个主成分。因此，我们有 l=1。所以矩阵 D 的形状为 (n×1)：它是一个简单的列向量。由于它是一个向量，我们将其称为 d：

因为我们将采用平方 L2 范数：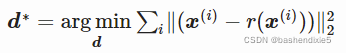

另。即第一个主成分

带入方程

由于约束 3.（D 的列有单位范数）我们有。 d 是 D 的列之一，因此具有单位范数。

我们可以使用矩阵 X 来收集所有观察结果，而不是使用沿 m 个数据点 x 的总和：

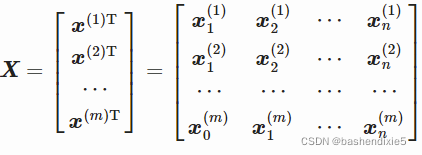
既有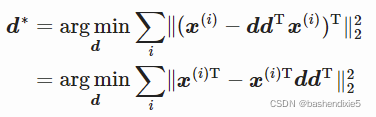

并且

8、使用迹运算符

我们现在将使用 Trace 算子来简化方程以最小化。

由于这里，故

由于我们可以在 Trace 中循环矩阵的顺序，我们可以这样写：

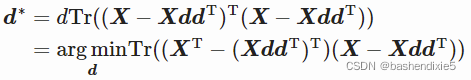
让我们把它代入我们的方程：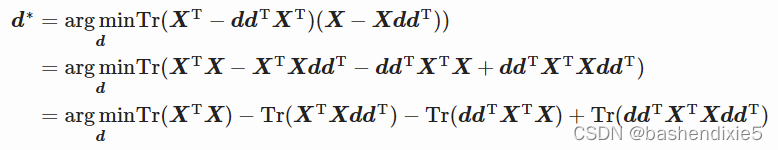

我们可以删除不依赖于 d 的第一项：

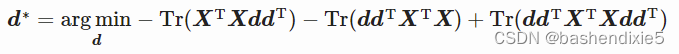
因为

简化得

即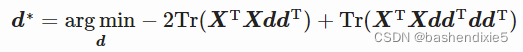

又因为

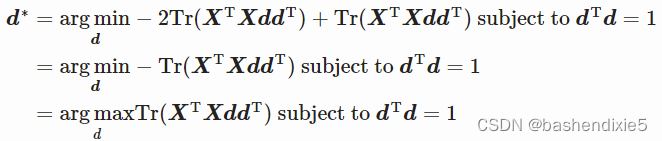
即

我们将看到我们可以通过计算的特征向量来找到函数的最大值。

9、协方差矩阵

正如我们上面所写的，最大化分量方差和最小化重构数据与实际数据之间的误差的优化问题是等价的。

如果我们将数据集中在0附近（即对数据中心化和规范化），则是协方差矩阵。

协方差矩阵是一个 n × n 矩阵（n 是维数）。它的对角线是对应维度的方差，其他单元格是两个对应维度之间的协方差（冗余量）。

这意味着我们在两个维度之间拥有的最大协方差，这些维度之间存在更多的冗余。这也意味着如果方差很高，则最佳拟合线与小误差相关联。最大化方差和最小化协方差（为了去相关维度）意味着理想的协方差矩阵是对角矩阵（仅对角线中的非零值）。因此，协方差矩阵的对角化将为我们提供最优解。

三、应用PCA示例

作为示例，我们创建一个 2D 数据集。为了查看 PCA 的效果，我们将介绍两个维度之间的一些相关性。让我们创建 100 个具有 2 个维度的数据点：

np.random.seed(123)
x = 5*np.random.rand(100)
y = 2*x + 1 + np.random.randn(100)

x = x.reshape(100, 1)
y = y.reshape(100, 1)

X = np.hstack([x, y])
X.shape

plt.plot(X[:,0], X[:,1], '*')
plt.show()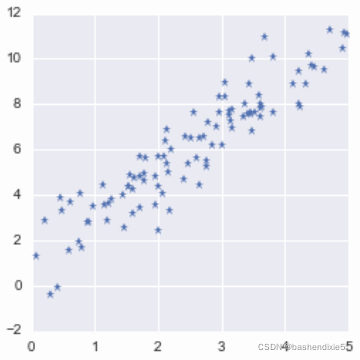

高度相关的数据意味着维度是冗余的。可以从另一个预测一个而不会丢失太多信息。

我们要做的第一个处理是将数据集中在 0 附近。PCA 是一个没有截距的回归模型，因此第一个分量必然穿过原点。

这是一个简单的函数，它将每列的平均值减去该列的每个数据点。它可用于将数据点集中在 0 附近。

def centerData(X):
    X = X.copy()
    X -= np.mean(X, axis = 0)
    return X

因此，让我们将两个维度的数据 X 都集中在 0 附近：

X_centered = centerData(X)
plt.plot(X_centered[:,0], X_centered[:,1], '*')
plt.show()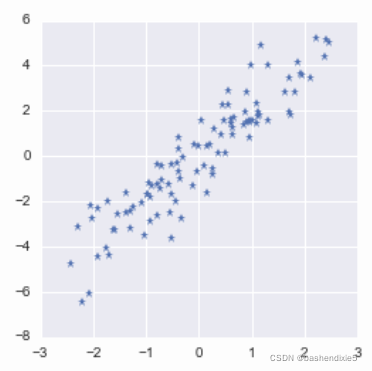

我们现在可以寻找主成分。我们看到它们对应于 d 取的最大化以下函数的值：

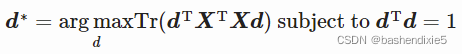
要找到 d，我们可以计算的特征向量。所以让我们这样做：

eigVals, eigVecs = np.linalg.eig(X_centered.T.dot(X_centered))
eigVecs

求得

array([[-0.91116273, -0.41204669],
       [ 0.41204669, -0.91116273]])

这些是最大化我们功能的向量。每个列向量都与一个特征值相关联。与较大特征值相关的向量告诉我们与数据中较大方差相关的方向。

首先，让我们创建一个函数 plotVectors() 来绘制向量：

def plotVectors(vecs, cols, alpha=1):
    plt.figure()
    plt.axvline(x=0, color='#A9A9A9', zorder=0)
    plt.axhline(y=0, color='#A9A9A9', zorder=0)

    for i in range(len(vecs)):
        x = np.concatenate([[0,0],vecs[i]])
        plt.quiver([x[0]],
                   [x[1]],
                   [x[2]],
                   [x[3]],
                   angles='xy', scale_units='xy', scale=1, color=cols[i],
                   alpha=alpha)

对数据重新可视化

orange = '#FF9A13'
blue = '#1190FF'
plotVectors(eigVecs.T, [orange, blue])
plt.plot(X_centered[:,0], X_centered[:,1], '*')
plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.show()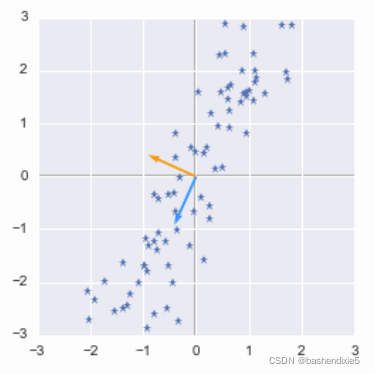

我们可以看到蓝色矢量方向对应于我们数据的倾斜形状。如果您将数据点投影在对应于蓝色矢量方向的线上，您最终会得到最大的方差。该向量具有最大化投影数据方差的方向。看看下图：

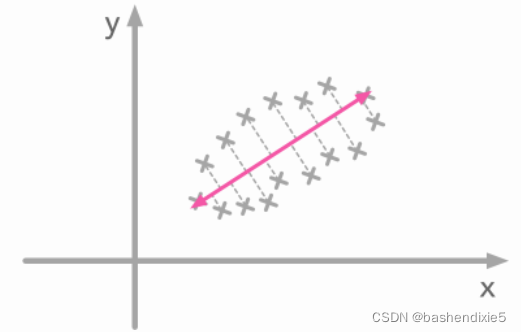
当您在粉红色线上投影数据点时，会有更多的差异。这条线的方向使数据点的方差最大化。上图也是一样：我们的蓝色向量具有数据点投影具有较高方差的线的方向。那么第二个特征向量与第一个特征向量正交。

在上图中，蓝色向量是第二个特征向量，所以让我们检查它是否与更大的特征值相关联：

eigVals得值为

array([  18.04730409,  798.35242844])

所以是的，第二个向量对应于最大的特征值。

现在我们已经找到了矩阵 d，我们将使用编码函数来旋转数据。旋转的目标是最终得到一个新的坐标系，其中数据不相关，因此基础轴收集所有方差。然后可以只保留几个轴：这是降维的目的。

D 是包含我们之前计算的特征向量的矩阵。此外，这个公式只对应一个数据点，其中维度是 x 的行。在我们的例子中，我们会将它应用于所有数据点，并且由于 X 在列上有维度，我们需要对其进行转置。

X_new = eigVecs.T.dot(X_centered.T)

plt.plot(eigVecs.T.dot(X_centered.T)[0, :], eigVecs.T.dot(X_centered.T)[1, :], '*')
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.show()

我们旋转了数据，以便在一个轴上具有最大的方差，旋转改变了我们的数据集，现在在一个基础轴上具有更多的方差。你可以只保留这个维度并且也极具代表性。

机器学习笔记 - 主成分分析中的数学