简单引入:
有一座高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。

动态规划中的三个概念:最优子结构,边界,状态转移公式;
F(1)=1;
F(2)=2;
F(n)=F(n-1)+F(n-2) (n>=3);
例如:F(10)=F(8)+F(9)为最优子结构;F(1)=1,F(2)=2为边界;F(n)=F(n-1)+F(n-2) (n>=3)为状态转移公式;
方法一:递归求解
//递归法求解
int getClimbingWays(int n)
{
if(n<1)
return 0;
if(n=1)
return 1;
if(n=2)
return 2;
return getClimbingWays(n-1)+getClimbingWays(n-2);
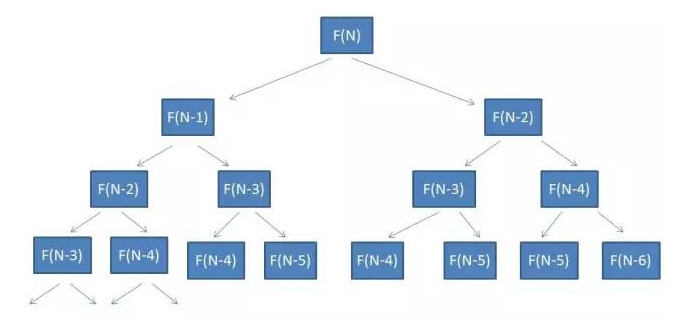
}求解过程类似下面二叉树,二叉树高度为N-1,节点个数接近于2的N-1次方,所以复杂度近似看作O(2^N);
这其中有太多的节点个数被重复计算,因此效率很低。因此我们可以先创建一个map来保存每次不同参数的计算结果,当遇到相同的参数时候,在从map中取出来,这样就不用重复计算了,叫做备忘录算法。
方法二:备忘录算法
//备忘录算法
int getClimbingWays(int n,map<int,int> &m)
{
if(n<1)
return 0;
if(n==1)
return 1;
if(n==2)
return 2;
if(m.find(n))
return m.at(n);
else
{
int value =getClimbingWays(n-1,m)+getClimbingWays(n-2,m);
m.insert(pair<int,int>(n,value));
return value;
}
}该算法的时间和空间的复杂度都为O(N);对于空间复杂度我们还可以进一步地优化,刚刚采用的是对F(N)自定向下做递归运算的,下面从自底向上求解,在每一次的计算迭代过程中,我们只需要保留之前的两个状态,就可以推导出新的状态,而不需要全部保存。下面就是动态规划法的实现:
方法三:动态规划
//动态规划法
int getClimbingWays(int n)
{
if(n<1)
return 0;
if(n==1)
return 1;
if(n==2)
return 2;
int a=1;
int b=2;
int temp=0;
for(int i=3;i<=n;i++)
{
temp=a+b;
a=b;
b=temp;
}
return temp;
}该方法时间复杂度是O(N),由于只引入了两三个变量,所以空间复杂度只有O(1);
二维动态规划问题:
题目:有5座金矿,10个工人,金矿价值分别为500金/5人,200金/3人,300金/4人,350金/3人,400金/5人
金矿数量设为N,工人数量设为W,金矿的黄金量设置g[ ],金矿的用工量设为p[ ];
状态转移方程式:
F(n,w) = 0 ; (n<=1,w<p[0]); 当工人数量不够第一个金矿的用量
F(n,w) = g[0]; (n==1,w>=p[0]); 当工人数量够第一个金矿的用量,但是只有一个金矿
F(n,w) = F(n-1,w); (n>1,w<p[n]);
F(n,w) =max{ F(n-1,w),F(n-1,w-p[n])+g[n]} (n>1,w>=p[n])
相关代码:
#include<iostream>
using namespace std;
const int MIN=0;
int F[200][200];//前i个物品装入容量为j的背包中获得的最大价值
int max(int a,int b) //一个大小比较函数,用于当总重大于第I行时
{
if(a>=b)
return a;
else
return b;
}
int Knapsack(int n,int w[],int v[],int x[],int C)//数组是当做指针传递的
{
int i,j;//F[i][j] 前i个物品装入容量为j的背包中获得的最大价值
for(i=0;i<=n;i++)
for(j=0;j<=C;j++)
F[i][j]=MIN; //初始化为0
//第一种写法
for(i=1;i<=n;i++)
for(j=w[i];j<=C;j++)//这里j是从w[i]开始,背包容量小于第i件物品重量,则状态转换方程中下标出现负值,无意义
{
F[i][j]=max(F[i-1][j],F[i-1][j-w[i]]+v[i]);//建立背包表
// cout<<"F["<<i<<"]["<<j<<"]="<<F[i][j]<<endl;
}
//第二种写法,易于理解
// for(i=1;i<=n;i++)
// for(j=1;j<=C;j++) //这里j是从1开始
// {
// if(j<w[i]) //背包容量小于第i件物品重量
// F[i][j]=F[i-1][j];
// else
// F[i][j]=max(F[i-1][j],F[i-1][j-w[i]]+v[i]);//建立背包表
// // cout<<"F["<<i<<"]["<<j<<"]="<<F[i][j]<<endl;
// }
j=C;//确定背包容量
for(i=n;i>0;i--) //已知背包容量,不断减去最大的物品重量来确定背包中装的物品
{
if(F[i][j]>F[i-1][j])//如果将前i个物品装进去比将前i-1个物品装进去总价值大,说明总价值最大的背包中有第i个物品。
{
x[i]=1;
j=j-w[i];//不用担心结果小于零,因为在上面的二重循环中已经处理过了
}
else
x[i]=0;
}
cout<<"选中的物品是:"<<endl;
for(i=1;i<=n;i++)
cout<<x[i]<<endl;
//也可以这样输出背包中的物品
// while(i)
// {
// if(F[i][j]==(F[i-1][j-w[i]]+v[i]))//逐个输出每个物品
// {
// cout<<i<<":"<<"v="<<v[i]<<",w="<<w[i]<<endl;
// j-=w[i];
// }
// i--;
// }
return F[n][C];
}
int main()
{
int s;//获得的最大价值
int n,i;
int C;//背包最大容量
int *w,*v,*x;
cout<<"请输入背包的最大容量:"<<endl;
cin>>C;
cout<<"物品数:"<<endl;
cin>>n;
//n+1是因为数组从1开始方便理解
//重量 价值 和物品的状态 均对应着存到数组中,物品从1开始。
w = new int[n+1]; //物品的重量
v = new int[n+1]; //物品的价值
x = new int[n+1]; //物品的选取状态 选中则是1 没选中为0
cout<<"请分别输入物品的重量:"<<endl;
for(i=1;i<=n;i++)
cin>>w[i];//w[0]空出
cout<<"请分别输入物品的价值:"<<endl;
for(i=1;i<=n;i++)
cin>>v[i];//v[0]空出
s=Knapsack(n,w,v,x,C); //调用核心函数
cout<<"最大物品价值为:"<<endl;
cout<<s<<endl;
delete []w;
delete []v;
delete []x;
system("pause");
return 0;
}当无法确定输入数量的时候,需要用回车符结束输入,开辟容量为100的数组,主函数代码如下:
int main()
{
int s;//获得的最大价值
int n;
int C;//背包最大容量
cout<<"请输入背包的最大容量:"<<endl;
cin>>C;
int W[100]={0};
int V[100]={0};
cout<<"请分别输入物品的重量:"<<endl;
int a;
n=1; //因为数组从1开始方便理解 重量 价值 和物品的状态 均对应着存到数组中,物品从1开始。
while(cin>>a)
{
W[n]=a;
n++;
if (getchar() == '\n') break; //通过回车判断跳出循环,如果没有该语句跳不出循环,因为cin会忽略跳过回车键
}
cout<<"请分别输入物品的价值:"<<endl;
int b;
n=1;
while(cin>>b)
{
V[n]=b;
n++;
if (getchar() == '\n') break;
}
int* x = new int[n+1]; //物品的选取状态 选中则是1 没选中为0
s=Knapsack(n,W,V,x,C); //调用核心函数
cout<<"最大物品价值为:"<<endl;
cout<<s<<endl;
delete []x;
system("pause");
return 0;
}参考链接:https://blog.csdn.net/sinat_22991367/article/details/51861373
注意:动态规划的时间复杂度是O(n*w),空间复杂度为O(w),所以当w远大于n时候,其效率还不如递归,时间复杂度只需要O(n*n)