动态规划解释
维基百科的定义:
- 动态规划的本质,是对问题状态的定义和状态转移方程的定义。引自维基百科
dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems.动态规划是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决。如何拆分问题,才是动态规划的核心。而拆分问题,靠的就是状态的定义和状态转移方程的定义。
什么样的问题适合使用动态规划 ?
(1) 满足动态规划的最优化原理:
作为整个过程的最优策略具有如下性质:无论过去的状态和决策如何,对前面的决策所形成的当前状态而言,余下的诸决策必须构成最优策略。 可以通俗地理解为子问题的局部最优将导致整个问题的全局最优,即问题具有最优子结构的性质,也就是说一个问题的最优解只取决于其子问题的最优解,非最优解对问题的求解没有影响。
(2)满足动态规划的无后效性原则:
所谓无后效性原则,指的是这样一种性质:某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响。也就是说,“未来与过去无关”,当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变。具体地说,如果一个问题被划分各个阶段之后,阶段 I 中的状态只能由阶段 I+1 中的状态通过状态转移方程得来,与其他状态没有关系,特别是与未发生的状态没有关系,这就是无后效性。
解题步骤是怎样?
1、状态的定义
2、状态转移方程的建立
状态即问题的子问题,之所以叫状态是为了防止混淆原问题,用计算机来表示就是用哪些变量存储哪些数据。状态转移方程,当状态定义好后,他们之间的转换关系就是状态转移方程,用计算机表示就是怎样根据一些变量计算出另一些变量。下面我将通过0-1背包问题来像大家解释以上概念,方便大家理解。
问题描述
现有n件物品和一个容量为c的背包。第i件物品的重量是重量为w[i],价值是v[i]。已知对于一件物品必须选择取(用1表示)或者不取(用0表示),且每件物品只能被取一次(这就是“0-1”的含义)。求放置哪些物品进背包,可使这些物品的重量总和不超过背包容量,且价值总和最大。
问题分析
这个问题特点是,每种物品只有一件,可以选择放或者不放, 假设我们从没见过这个题,所以我们要先分析下是不是适合使用动态规划,先从第一点来看是不是符合最优子结构。设背包最大容量C,如果某个状态的最优解包含了物品n,那么其余X1、X2、…Xn-1 一定构成了子问题1,2,…n-1在容量为C-cn适合的最优解,如果这个最优解不包含物品n,那么其他X1…Xn-1 一定构成了子问题 1、2…n-1在容量为C时候的最优解。我们可以用反证法来证明上述,如果在某个状态的最优解包含了物品n,如果在其余X1、X2、…Xn-1
没有构成子问题1,2,…n-1在容量为C-cn适合的最优解,那么必定存在一个其他组合方式能使该子问题达到最优解的,那么这就与题目1、2…n-1在容量为C时候的最优解冲突了。因为假设某个问题最优解包含了物品n的时候的价值是8,体积为8,如果去掉物品n后价值为5,体积为5,如果其他物品没有构成在体积为5下的最优解的话,那么就存在其他组合方式能让体积为5的时候价值大于5,那么再加上物品n的话总价值就会大于8,与假设不符,因为假设是8为最优。所以通过上述分析,该问题是具备最优子结构性质的。
那么再来看看是不是符合无后效性,当你知道物品总体积为C的时候你想加入一个cn,所以加入之前体积为C-cn,假设价值为x,加入后价值为y,你根本不用管这x怎么来的,到底是加入了哪些物品才得到了x,这些你都不用管,因为y的得到只需要x加上物品n的价值就行了,不关心你怎么来的,所以x为以前历史的一个总结。
解题
int c[N]; //存储物体体积
int v[N];//存储物体价值
int i,j; //物品序号、当前体积。
1、状态定义
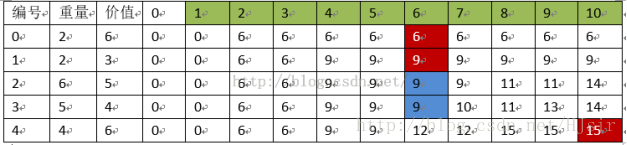
我们可以先这样考虑,当背包容量为1时,如何放置物品才能使背包中价值最大;同样当背包容量为2时,如何放置能使背包中价值最大,以此类推,直到背包容量为10。此时我们需要维护一张二维表m[i][j],其中横坐标i表示物品,纵坐标表示背包容量(1<=j<=10)。
0-1背包问题的递推二维表
可以将每个重量的时候看成是一个状态。
2、状态转移方程式建立
通过上表可以看到,当横坐标到了一定体积的时候,如果当前c[i]小于j,那么就可以选择加入 或者不加入,如果加入后总价值比原来的大,那么肯定加进去,如果没有原来大则不加。当前价值为m[i-1][j],加入前价值为m[i-1][j-c[i]],加入后价值为加入前加上物品重价值,即m[i-1][j-c[i]+v[i],通过上述便可建立状态转移方程式了。
(1)i=0 当j<c[0]时,m[0][j]=0;当j>=c[0]时,m[0][j]=v[0]。
(2)i>0 当j<c[i],m[i][j]=m[i-1][j];当j>=c[i],m[i][j]=max{m[i-1][j-c[i]]+v[i],m[i-1][j]}。
编码
这儿我只列出核心算法代码
for(int i=1;i<N;i++){
for(int j=1;j<=C;j++){
if(c[i]<j){ //可以加入
m[i][j]= max(m[i-1][j],m[i-1][j-c[i]]+v[i]);
}else{ //加不进
m[i][j]=m[i-1][j];
}
}
}总结
至此利用0-1背包问题谈动态规划已经结束了。总结一下,其实动态规划是用来解决一类问题的,其核心应该是状态定义,而不是状态转移方程式的建立。一个问题状态的定义有很多种,状态转移方程式也有很多种,甚至存在一个有后效性的定义,但是并不代表不能用动态规划,只是不适合罢了。动态规划是寻找一种对问题的观察角度,让问题能够以地推或者分治的方式去解决。所以寻找看问题的角度,才是动态规划中最耀眼的宝石。
感谢