案例

假如我们现在在设计一个英文翻译程序，要把英文翻译成汉语，显然我们需要知道每个单词对应的汉语意思。我们可以建立一颗二分搜索树来实现英语到汉语的关联。为了更快速地翻译，我们可以使用AVL树或者红黑树使每次查询的时间复杂度Θ(lgn)，实际上对于字典翻译程序来说这么做存在一个问题，比如“the”这个单词经常用，却很有可能存在于十分远离树根的位置，而“machicolation”这种不常用的单词很可能存在于十分靠近树根的位置，这就导致查询频率高的单词需要的查询时间更长，而查询频率很低的单词查询时间却很短。这明显不符合我们的期望，我们希望高频率的单词用更少的时间查询到，低频率的单词则用相对更长的时间查询到，也就是高频单词靠近树根，而低频单词远离树根。这时，我们就需要一颗最优二分搜索树来解决这个问题。

最优二分搜索树

何为最优二分搜索树

给定一个组长度为n关键字的有序序列K=< k1, k2, k3 ···· kn >
以及对应关键字的出现概率P=< p1, p2, p3 ···· pn >
由于我们要检索的关键字可能不在树中，所以我们需要n+1个伪关键字
给定一组长度为n+1的伪关键字D=< d0, d1, d2 ···· dn >
其中d0表示小于任何一个关键字的值，dn表示大于任何一个关键字的值，当 i != 0 && i != n 时，di
表示所有大于ki且小于ki+1的不存在于序列K中的值的集合（不考虑值相等的情况）（比如d5就表示所有大于k5且小于k6的不存在于序列K中的值的集合）

若满足下列条件则该二分搜索树为一颗最优二分搜索树

是一颗二分搜索树（废话）
满足下列条件

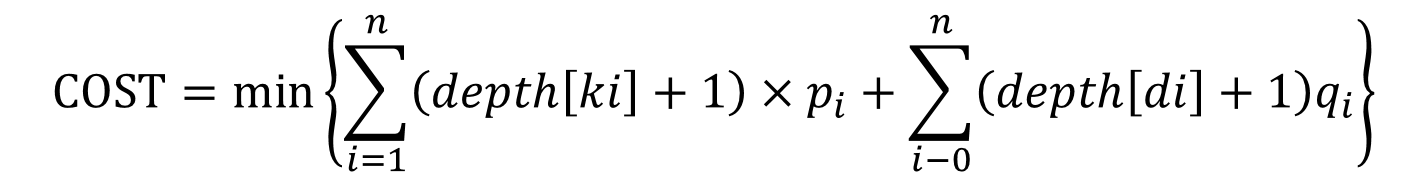
注意

最优二分搜索树不一定是一颗平衡二分搜索树
最优二分搜索树的根节点不一定是出现频率最高的节点

例子

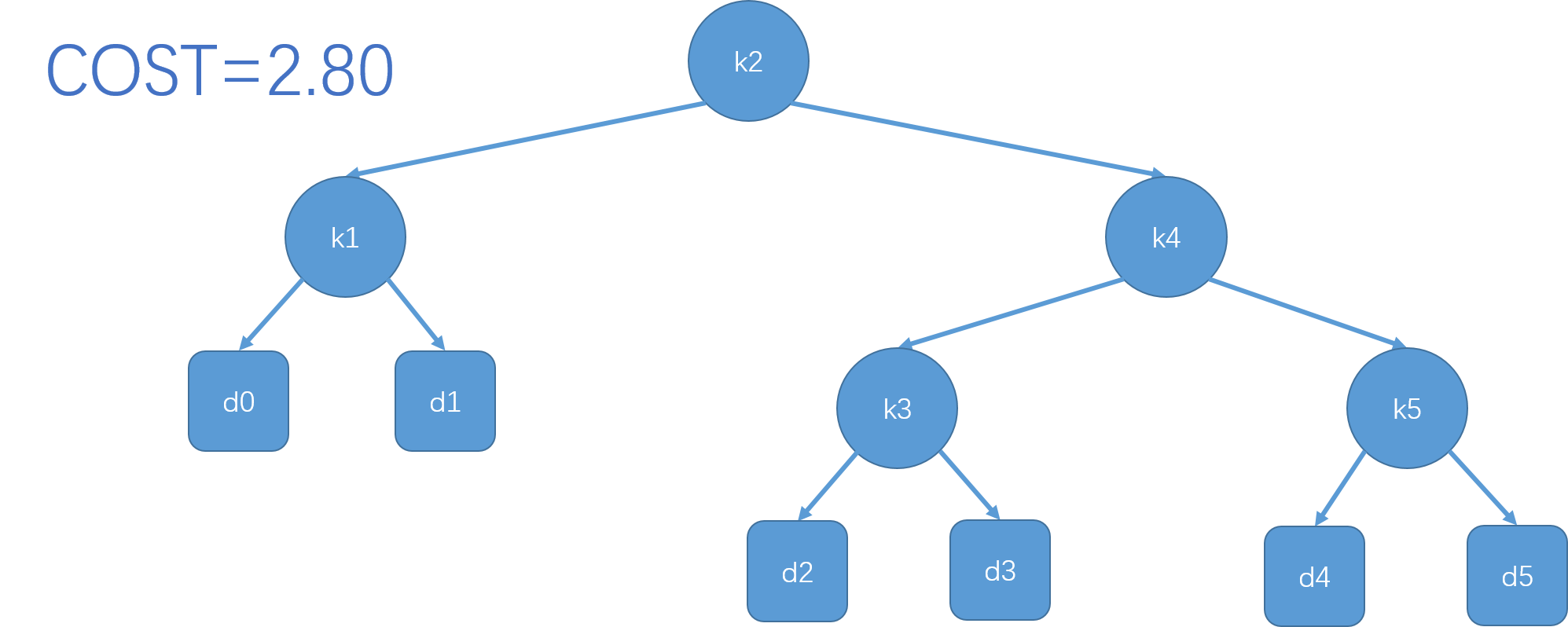
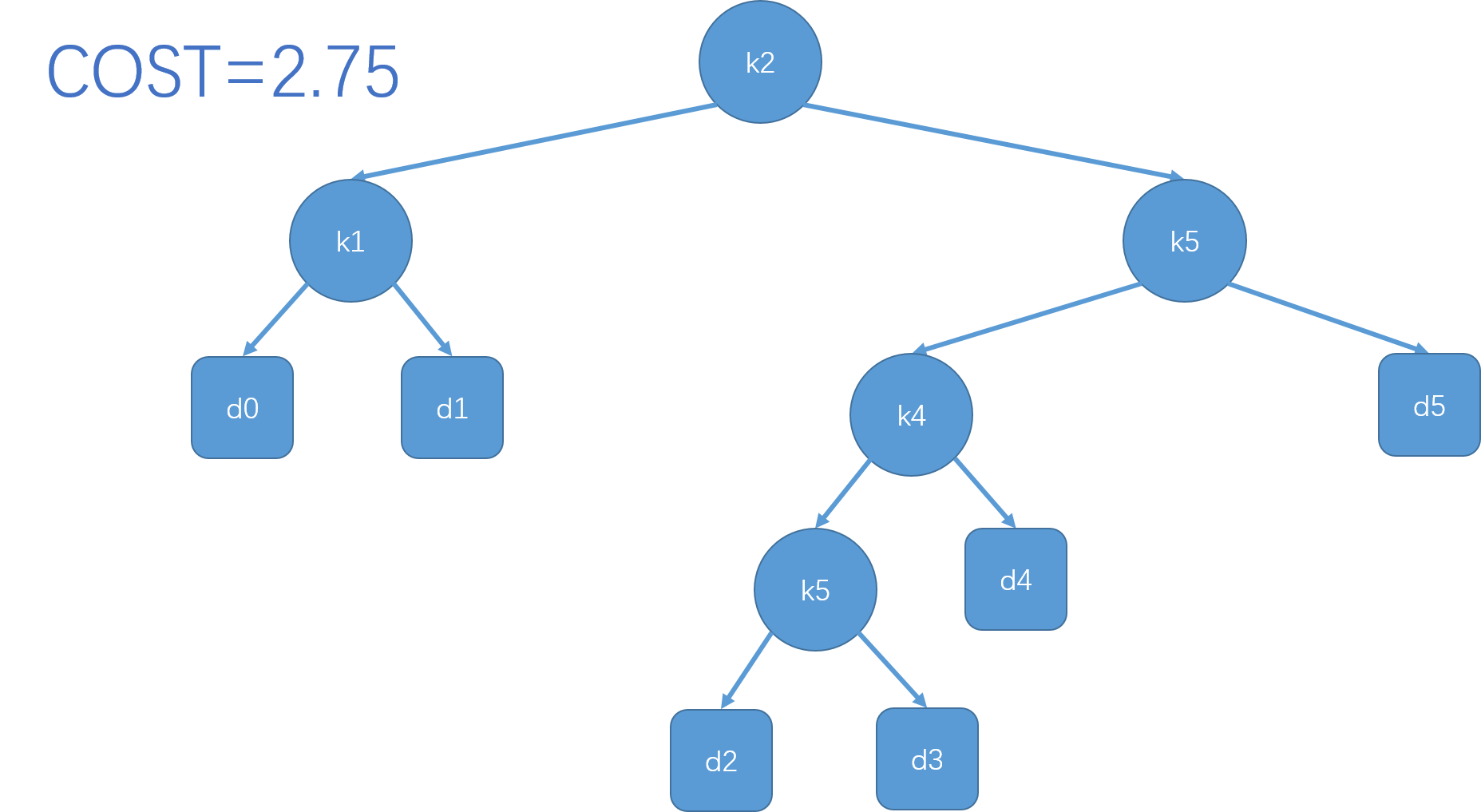
最优二分搜索树

如何构建一颗最优二分搜索树

穷举法

如果要一个一个地去穷举出所有的形态再从中挑选时空复杂度很大，一个有n的节点的二叉树的形态有很明显如果穷举的话是非常不划算的。

动态规划

是否可以使用

既然穷举法不行那么动态规划是否适用呢？使用动态规划需要两个条件

具有优化子结构
具有重叠子问题

这里可以直接给出最优二分搜索树问题的优化子结构：对于一颗最优二分搜索树T，其任意一颗子树T1一定是一颗最优二分搜索树。这里可以用反证法证明，T是一颗最优二分搜索树，如果存在一个子树T1不是最优二分搜索树，那么将此子树替换为包含关键字相同但是形态不相同的另外一颗子树T2，就很有可能使的整棵树T的期望搜索代价更低，这就不满足T是一颗最优二分搜索树的前提。

根据上述的分析，可以知道最优二分搜索树问题是存在重叠子问题的，因为如果我们要构造一颗最优二分搜索树，必须优先构造其子树，构造其子树的时候要构造其子树的子树，如此下去，就存在了重叠的子问题。

因此最优二分搜索树问题是可以使用动态规划求解的。

问题分析

值得注意的是，如果i=j-1，这颗子树实际上不包含任何实际的关键字，但是会包含为关键字di-1（所有小于ki的不存在于序列K中的数字的集合）。这个问题我们并没有明显的规律可循，所以我们只能寻找一个关键字kr（i <= r <= j）,当kr作为该子树的树根时期望搜索代价最低，只能一个一个地试。

我们以COST[i][j]表示包含关键字 ki ···· kj 的子树的搜索代价
我们以W[i][j]表示包含关键字 ki ···· kj 以及伪关键字 di-1 ···· dj的子树的每个关键字和伪关键字的概率和

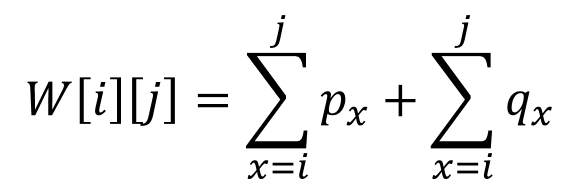
递归式

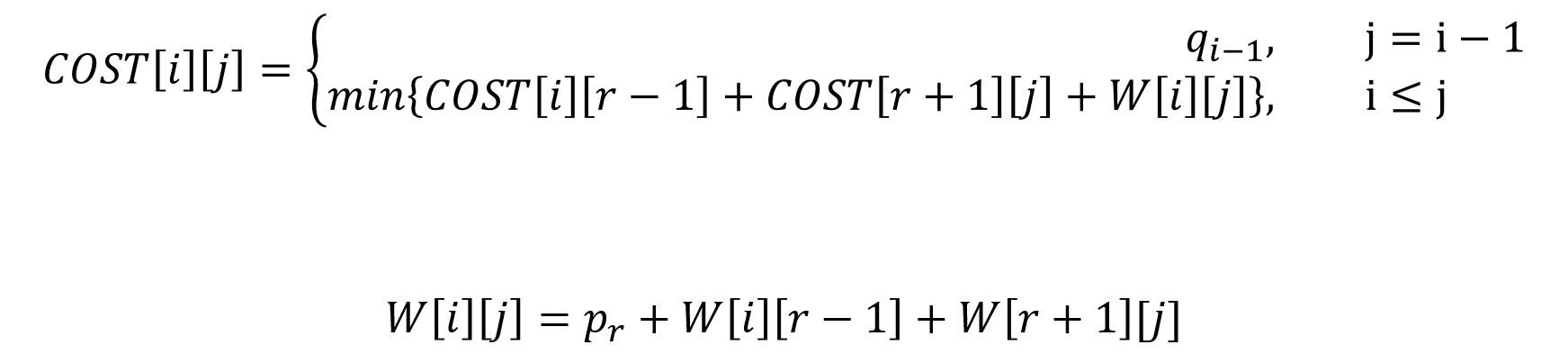
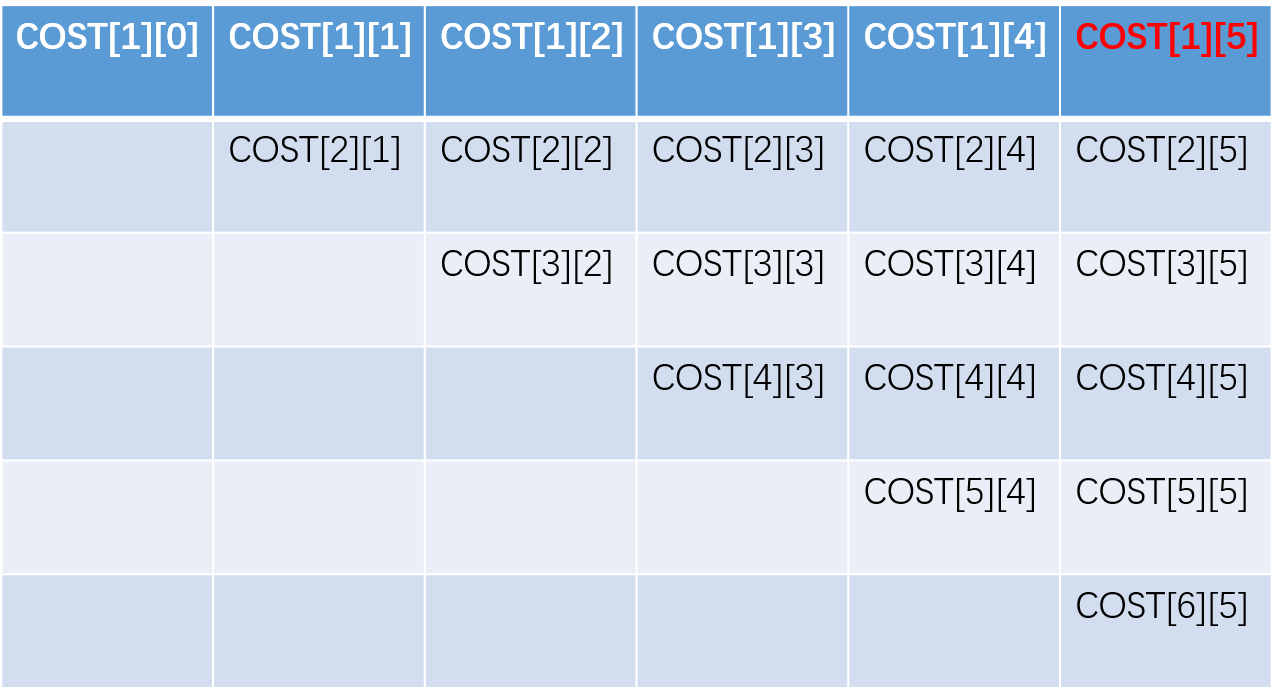
子问题求解顺序（矩阵填充方式）

子问题矩阵如图

应该按照对角线方式进行填充，因为每次求解一个对角线上的子问题，都需要前一个对角线的结果

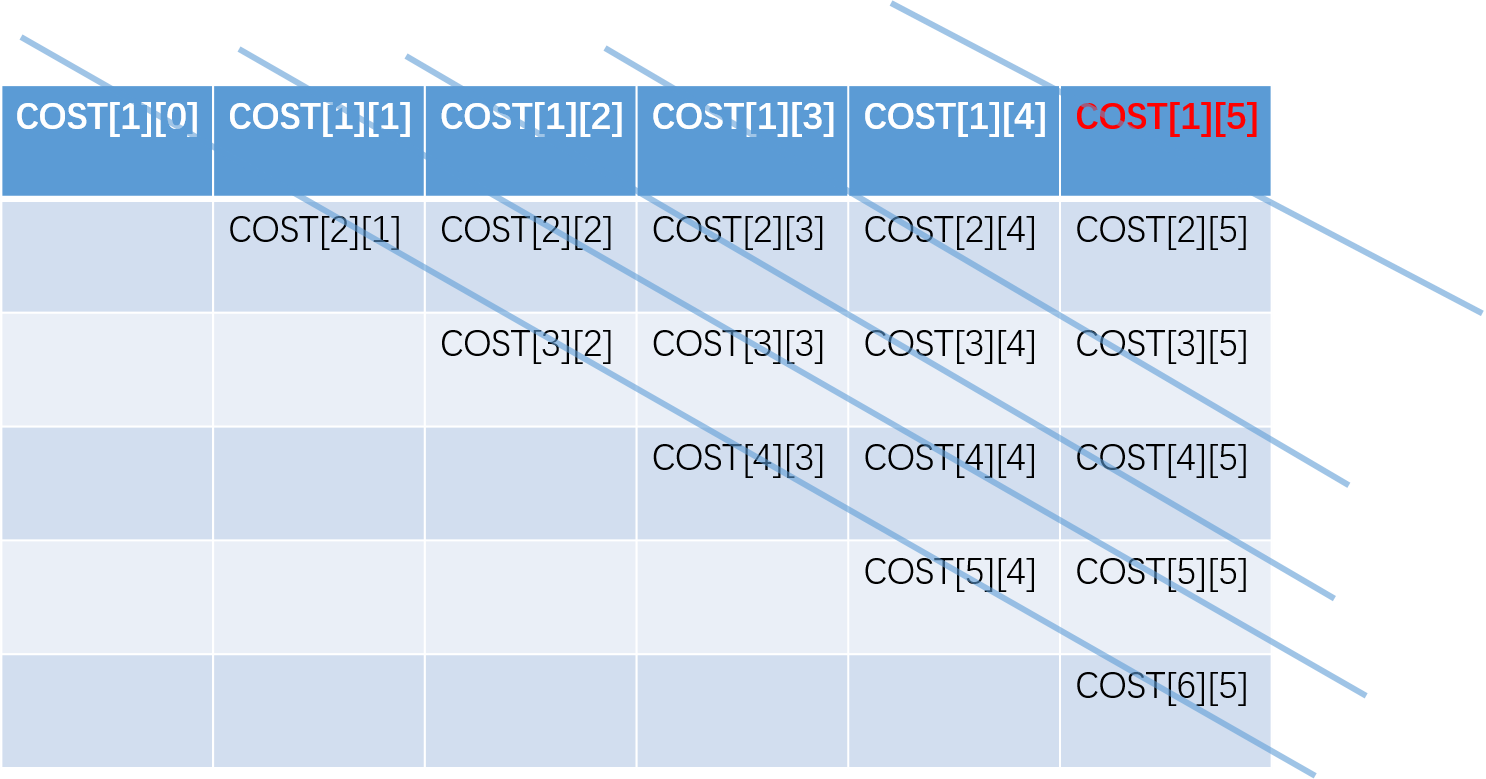
本文涉及两个矩阵，两个矩阵的填充方式相同

C++代码

#include <iostream>
#include <string>
#include <algorithm>
#include <map>

using namespace std;
const double INF = 99999;

void OPTIMAL_BST(double* p, double* q, int n);

int main()
{
    int n;
    cin >> n;
    double* p = new double[n + 1];
    double* q = new double[n];
    for (int i = 1; i <= n; i++)
        cin >> p[i];
    for (int i = 0; i <= n; i++)
        cin >> q[i];
    OPTIMAL_BST(p, q, n);
    delete p, q;
    system("pause");
}

void OPTIMAL_BST(double* p, double* q, int n)
{
    double** e = new double*[n + 2];
    double** w = new double*[n + 2];
    double t = 0.0;
    //int** root = new int*[n + 2];
    int j = 0;
    for (int i = 0; i <= n + 1; i++)
    {
        e[i] = new double[n + 1];
        w[i] = new double[n + 1];
        //root[i] = new int[n + 1];
        //矩阵置零
        memset(e[i], 0, sizeof(double)*(n + 1));
        memset(w[i], 0, sizeof(double)*(n + 1));
        //memset(root[i], 0, sizeof(int)*(n + 1));
    }

    //填充第一个对角线
    for (int i = 1; i <= n + 1; i++)
    {
        e[i][i - 1] = q[i - 1];
        w[i][i - 1] = q[i - 1];
    }
    for (int k = 1; k <= n; k++)
    {
        for (int i = 1; i <= n - k + 1; i++)
        {
            j = i + k - 1;
            e[i][j] = INF;
            w[i][j] = w[i][j - 1] + p[j] + q[j];

            for (int r = i; r <= j; r++)
            {
                t = e[i][r - 1] + e[r + 1][j] + w[i][j];
                if (e[i][j] - t > 0.0001)
                {
                    e[i][j] = t;
                    //root[i][j] = r;
                }
            }
        }
    }
    cout << endl << endl;
    for (int i = 1; i <= n + 1; i++)
    {
        for (int j = 0; j <= n; j++)
            cout << e[i][j] << '\t';
        cout << endl << endl << endl;
    }
    delete e, w;
    //delete root;
}

《算法导论》动态规划—最优二分搜索树

案例