目录
(一) 定义
树(Tree): 是一种动态的数据结构. 它是由 n(n>=1) 个有限结点组成一个具有层次关系的集合. 也可以认为树是由根结点和若干颗子树构成的. 其中:
- 结点(node): 树中存储的每个元素成为结点
- 根结点(roont): 有且只有一个没有父结点的结点被称为根结点或树根
- 度: 一个结点含有的子结点的个数
- 结点的层次: 从根开始定义起, 根为第1层, 根的子结点为第2层, 以此类推
- 树的高度或深度: 树中结点的最大层次
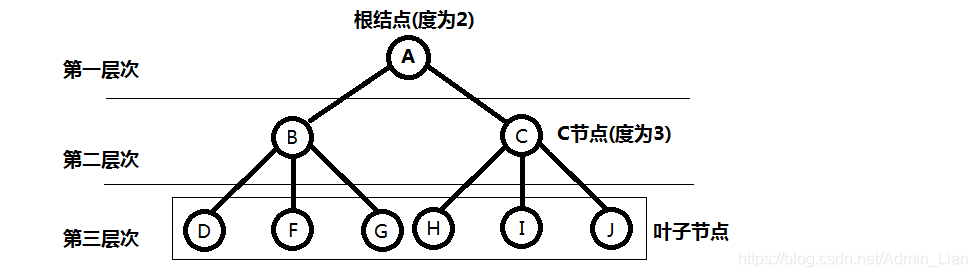
二叉树(Binary Tree): 是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成, 其中:
- 每个结点最多有两颗子树,所以二叉树中不存在度大于2的结点
- 二叉树的子树有左右之分,其次序不能任意颠倒
- 即使树中某结点只有一棵子树,也要区分它是左子树还是右子树
二叉树的种类:
- 满二叉树: 所有叶结点同处于最底层, 非叶子结点的度一定是2

- 完全二叉树: 叶结点只能出现在最后两层,且最底层叶结点均处于次底层叶结点的左侧.因此如果结点度为1,则该结点只有左孩子,即没有右子树(按照元素顺序排列成树的形状)
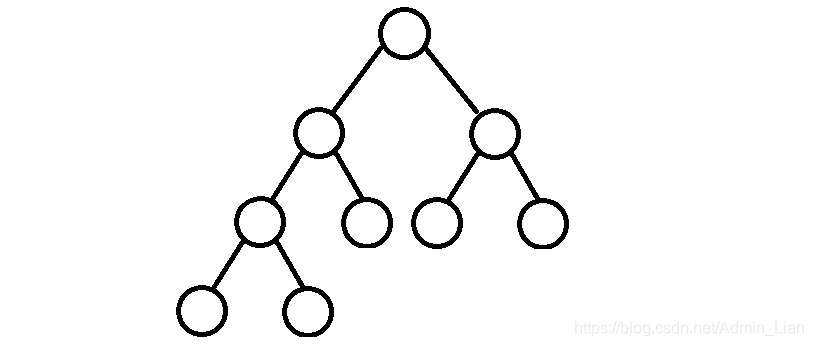
- 二分搜索树: 也是二叉树的一种, 且二分搜索树的每个结点的值大于其左子树的所有结点的值, 小于其右子树的所有结点的值. 二分搜索树的每一课子树也是二分搜索树. 存储的元素必须有可比性.
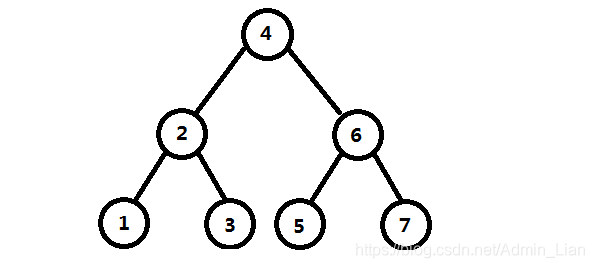
(二) 自定义二分搜索树BinarySearchTree
1. 新建自定义二分搜索树类BinarySearchTree
E 泛型继承Comparable<E>类: 保证了存储的元素必须有可比性
public class BinarySearchTree<E extends Comparable<E>> {
/**
* 节点内部类: 可以单独定义出来, 但用户无需关注二分搜索树实现, 因此定义成BinarySearchTree的内部类
*
* @author Administrator
*
*/
private class Node {
/**
* 存储的数据
*/
public E e;
/**
* 左子树
*/
public Node left;
/**
* 右子树
*/
public Node right;
public Node(E e) {
this.e = e;
this.left = null;
this.right = null;
}
}
/**
* 根结点
*/
private Node root;
/**
* 二分搜索树的元素个数
*/
private int size;
public BinarySearchTree() {
this.root = null;
this.size = 0;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
}
2. 自定义二分搜索树的增加操作
- 向二分搜索树种添加新的元素e, 如果添加相同的元素, add(e)直接返回
public void add(E e) {
// 二分搜索树为空, 新元素e作为二分搜索树的根结点
if(root == null) {
root = new Node(e);
size++;
} else {
add(root, e);
}
}
/**
* 向以node为根的二分搜索树中插入元素E, 递归算法
*
* @param node
* @param e
*/
private void add(Node node, E e) {
/*
* 递归的终止条件:
* 1.插入相同的元素
* 2.插入的元素小于当前节点存储的元素且当前节点的左子树为null
* 3.插入的元素大于当前节点存储的元素且当前节点的右子树为null
*/
if (e.equals(node.e)) {
return;
} else if (e.compareTo(node.e) < 0 && node.left == null) {
node.left = new Node(e);
} else if (e.compareTo(node.e) > 0 && node.right == null) {
node.right = new Node(e);
}
if (e.compareTo(node.e) < 0) {
add(node.left, e);
} else {
add(node.right, e);
}
}
递归算法add(node, e) 存在的问题:
- 在递归的过程中e和node.e, 比较了两次.
- 递归的终止条件过于臃肿: 既要比较e和node.e, 又还要判断左右子树是否为空, 且此递归并没有递归到二分搜索树的最底. 因为 Null 本身也是一课二叉树. 而当前递归操作左右子树为空时, 就达到了递归的终止条件了.
- 优化add(E e)方法:
/**
* 向二分搜索树种添加新的元素e
*
* @param e
*/
public void add(E e) {
root = add(root, e);
}
/**
* 向以node为根的二分搜索树中插入元素E, 返回插入新节点后二分搜索树的跟
* 递: 遍历符合的结点node二分搜索树, 找到添加元素的结点null
* 终止: node结点为空, 创建新元素结点, 并返回
* 归: 重新构建含有新元素结点的子树, 最终返回整棵二分搜索树
*
* @param node
* @param e
* @return
*/
private Node add(Node node, E e) {
// 递归的终止条件: node根结点为空
if (node == null) {
size++;
return new Node(e);
}
// 判断添加的元素 和 当前根节点元素 的大小
if (e.compareTo(node.e) < 0) {
// 重新构建当前根结点的左子树 等于 插入新节点后二分搜索树的跟
node.left = add(node.left, e);
} else if (e.compareTo(node.e) > 0) {
// 重新构建当前根结点的右子树 等于 插入新节点后二分搜索树的跟
node.right = add(node.right, e);
}
return node;
}
3. 自定义二分搜索树的查询操作
- 二分搜索树是否包含元素e
/**
*二分搜索树是否包含元素e
*
* @param e
* @return
*/
public boolean contains(E e) {
return contains(root, e);
}
/**
* 以node为根的二分搜索树是否包含元素e
* 递: 遍历符合的结点node二分搜索树
* 终止: node结点为空并返回false 或者 二分搜索树包含元素e并返回true
* 归: 无归 (相当于循环遍历: while(node != null) {node = node.left || node = node.right} )
*
* @param node
* @param e
* @return
*/
private boolean contains(Node node, E e) {
// 递归的终止条件: node为Null 和 二分搜索树包含元素e
if (node == null) {
return false;
}
if(e.compareTo(node.e) == 0) {
return true;
} else if (e.compareTo(node.e) < 0) {
return contains(node.left, e);
} else {
return contains(node.right, e);
}
}
- 覆盖重写toString()方法
@Override
public String toString() {
StringBuilder res = new StringBuilder();
generateTreeString(root, 0, res);
return res.toString();
}
/**
* 生成以node为根结点, 深度为depth的描述二叉树的字符串(中序遍历输入)
*
* @param node
* @param depth
* @param res
*/
private void generateTreeString(Node node, int depth, StringBuilder res) {
if (node == null ) {
res.append(generateDepthString(depth) + "null\n");
return;
}
generateTreeString(node.left, depth + 1, res);
res.append(generateDepthString(depth) + node.e + "\n");
generateTreeString(node.right, depth + 1, res);
}
/**
* 生成表达深度depth的字符串
*
* @param depth
* @return
*/
private String generateDepthString(int depth) {
StringBuilder res = new StringBuilder();
for (int i = 0; i < depth; i++) {
res.append("--");
}
return res.toString();
}
测试
public static void main(String[] args) {
BinarySearchTree<Integer> tree = new BinarySearchTree<>();
int[] nums = new int[] {4, 2, 6, 1, 3, 5, 7};
for (int i = 0; i < nums.length; i++) {
tree.add(nums[i]);
}
System.out.println(tree);
}
左边中序遍历输出的镜像就是右边的二分搜索树的树状图
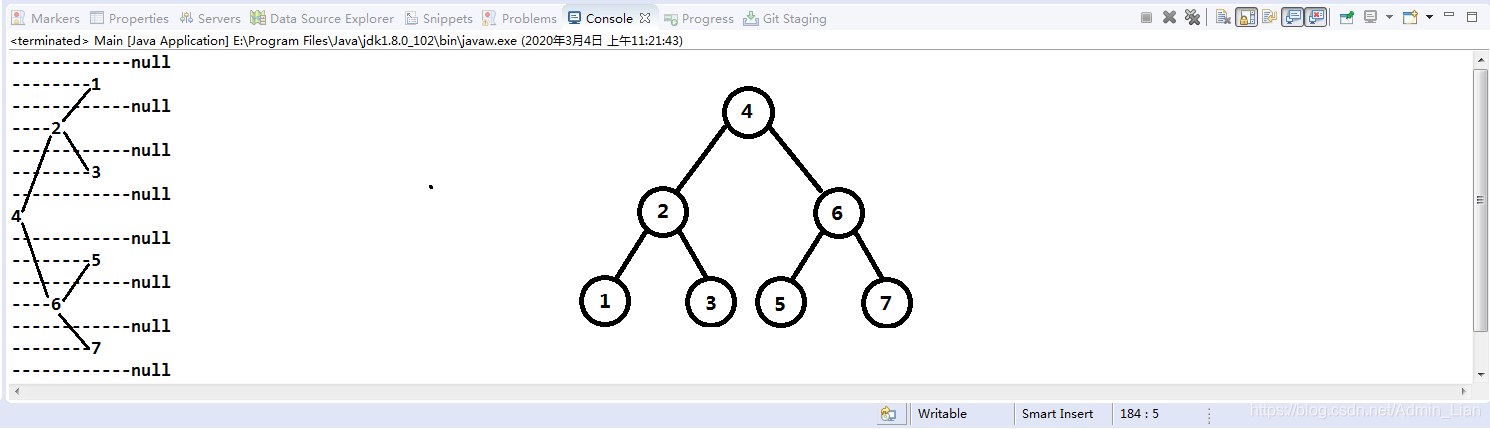
4. 自定义二分搜索树的遍历操作
- 前序遍历(深度优先遍历): 先输出根节点,然后输出左子树,最后输出右子树
/**
* 二分搜索树的前序遍历
*/
public void preOrder() {
preOrder(root);
System.out.println();
}
/**
* 前序遍历以node为根的二分搜索树, 递归算法
* 递: 遍历以node为根的二分搜索树, 打印输出node.e
* 终止: node结点为空
* 归: 无归 (相当于循环遍历: while(node != null) {node = node.left || node = node.right} )
*
* @param node
*/
private void preOrder(Node node) {
if (node == null) {
return;
}
System.out.println(node.e + " ");
preOrder(node.left);
preOrder(node.right);
}
- 中序遍历(深度优先遍历): 先输出左子树,然后输出根节点,最后输出右子树
/**
* 二分搜索树的中序遍历
*/
public void inOrder() {
inOrder(root);
System.out.println();
}
/**
* 中序遍历以node为根的二分搜索树, 递归算法
* 递: 遍历以node为根的二分搜索树, 打印输出node.e
* 终止: node结点为空
* 归: 无归 (相当于循环遍历: while(node != null) {node = node.left || node = node.right} )
*
* @param node
*/
private void inOrder(Node node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.print(node.e + " ");
inOrder(node.right);
}
- 前序遍历(深度优先遍历): 先输出左子树,然后输出右子树,最后输出根节点
/**
* 二分搜索树的后序遍历
*/
public void postOrder() {
postOrder(root);
System.out.println();
}
/**
* 后序遍历以node为根的二分搜索树, 递归算法
* 递: 遍历以node为根的二分搜索树, 打印输出node.e
* 终止: node结点为空
* 归: 无归 (相当于循环遍历: while(node != null) {node = node.left || node = node.right} )
*
* @param node
*/
private void postOrder(Node node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.print(node.e + " ");
}
- 层序遍历(广度优先遍历): 按照结点的层次从左到右遍历
/**
*二分搜索树的层序遍历(广度优先遍历): 借助队列数据结构来实现(先进先出)
*/
public void levelOrder() {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()) {
Node cur = queue.remove();
System.out.print(cur.e + " ");
if(cur.left != null) {
queue.add(cur.left);
}
if(cur.right != null) {
queue.add(cur.right);
}
}
System.out.println();
}
测试
public static void main(String[] args) {
BinarySearchTree<Integer> tree = new BinarySearchTree<>();
int[] nums = new int[] {4, 2, 6, 1, 3, 5, 7};
for (int i = 0; i < nums.length; i++) {
tree.add(nums[i]);
}
System.out.print("前序遍历: ");
tree.preOrder();
System.out.print("中序遍历: ");
tree.inOrder();
System.out.print("后序遍历: ");
tree.postOrder();
System.out.print("层序遍历: ");
tree.levelOrder();
}

5. 自定义二分搜索树的删除操作
- 删除二分搜索树的最小元素
/**
*寻找二分搜索树的最小元素
*/
public E minimum() {
if (size == 0) {
throw new IllegalArgumentException("BinarySearchTree is empty.");
}
return minimum(root).e;
}
/**
* 返回以node为根的二分搜索树的最小值所在的结点
*
* @param node
* @return
*/
private Node minimum(Node node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
}
/**
* 删除二分搜索树的最小元素
*
* @return
*/
public E removeMin() {
E res = minimum();
root = removeMin(root);
return res;
}
/**
* 向以node为根的二分搜索树中删除最小元素, 返回删除最小元素节点后二分搜索树的跟
* 递: 遍历左子树以node为根的二分搜索树, 找到要删除元素的结点
* 终止: node结点的左子树为空(最小元素结点), 返回 最小元素结点的 右子树
* 归: 根据返回值 重新构建 删除结点的父节点的左子树, 最终返回整棵二分搜索树
*
* @param node
* @return
*/
private Node removeMin(Node node) {
// 递归终止条件: node结点的左子树为空(最小元素结点)
if (node.left == null) {
// 返回 要输出最小元素结点的 右子树
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 根据返回值 重新构建 删除结点的父节点的左子树
node.left = removeMin(node.left);
return node;
}
- 删除二分搜索树的最大元素
/**
* 寻找二分搜索树的最大元素
*/
public E maximun() {
if (size == 0) {
throw new IllegalArgumentException("BinarySearchTree is empty.");
}
return maximun(root).e;
}
/**
* 返回以node为根的二分搜索树的最小值所在的结点
* 递: 遍历以node为根的右子树
* 终止: 当前node结点的右子树结点为空, 返回该节点
* 归: 无归
*
* @param node
* @return
*/
private Node maximun(Node node) {
if (node.right == null) {
return node;
}
return maximun(node.right);
}
/**
* 删除二分搜索树的最大元素
*
* @return
*/
public E removeMax() {
E res = maximun();
root = removeMax(root);
return res;
}
/**
* 向以node为根的二分搜索树中删除最大元素, 返回删除最大元素节点后二分搜索树的跟
* 递: 遍历右子树以node为根的二分搜索树, 找到要删除元素的结点
* 终止: node结点的右子树为空(最大元素结点), 返回 最大元素结点的 左子树
* 归: 根据返回值 重新构建 删除结点的父节点的右子树, 最终返回整棵二分搜索树
*
* @param node
* @return
*/
private Node removeMax(Node node) {
if (node.right == null) {
Node res = node.left;
node.left = null;
size--;
return res;
}
node.right = removeMax(node.right);
return node;
}
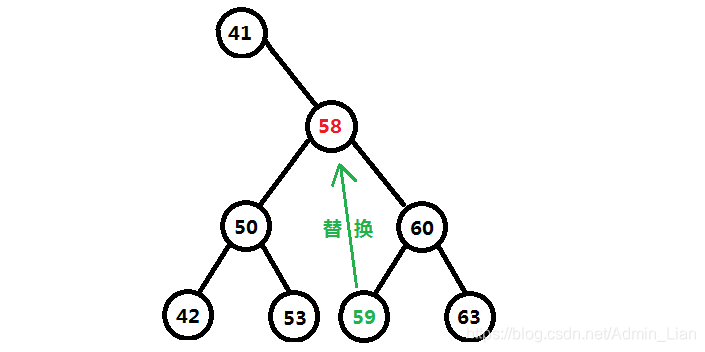
- 从二分搜索树中删除元素为e的结点
public void remove(E e) {
root = remove(root, e);
}
/**
* 删除以node为根的二分搜索树中值为e的结点, 返回删除结点后新的二分搜索树的根
* 递: 遍历符合的结点node二分搜索树, 找到要删除元素的结点
* 终止: node结点为空(不存在元素e) 和 找到要删除元素e的结点, 返回删除元素结点的替代结点
* 归: 重新构建含有替代结点的子树, 最终返回整棵二分搜索树
*
* @param node
* @param e
* @return
*/
private Node remove(Node node, E e) {
// 递归终止条件: node结点为空(不存在元素e) 和 找到要删除元素e的结点
if (node == null) {
return null;
}
if (e.compareTo(node.e) == 0) {
// 要删除结点的左子树为空, 返回 删除结点的右子树
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 要删除结点的右子树为空, 返回 删除结点的左子树
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 要删除结点的左右子树都不为空
// 找到要删除结点的替代者: 要删除结点的右子树中最小元素结点
Node replacerNode = minimum(node.right);
// 移除要删除结点的右子树中最小元素结点, 返回删除最小元素节点后二分搜索树的跟 作为 替代者的右子树
replacerNode.right = removeMin(node.right);
// 替代者的左子树 等于 要删除结点的左子树
replacerNode.left = node.left;
// 要删除的结点 与 二分搜索树 解耦
node.left = node.right = null;
return replacerNode;
} else if (e.compareTo(node.e) < 0) {
node.left = remove(node.left, e);
return node;
} else {
node.right = remove(node.right, e);
return node;
}
}
(三) 时间复杂度分析
二分搜索树的无论是添加操作add(e), 删除操作remove(e) 还是查询操作contains(e), 都是在二分搜索树中找到合适的结点再进行逻辑操作. 如图:
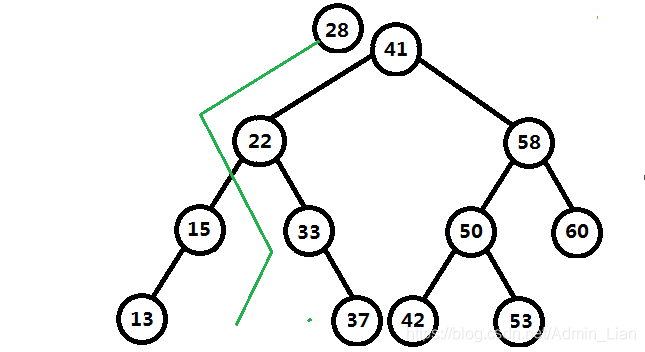
添加元素28所要找到合适的结点, 必须经过结点: 41 -> 22 -> 33. 由此看来在找适到合结点所要经历的最多个数结点为 树的高度h. 因此二分搜索树的添加操作, 删除操作, 查询操作的时间复杂度都为 O(h).
h高度为树结构特有的属性, 因此需要知道h与元素个数n之间的关系: 假设n个结点的二分搜索树为满二叉树(最理想情况, 且二分搜索树最坏的情况有可能退化成链表O(n))
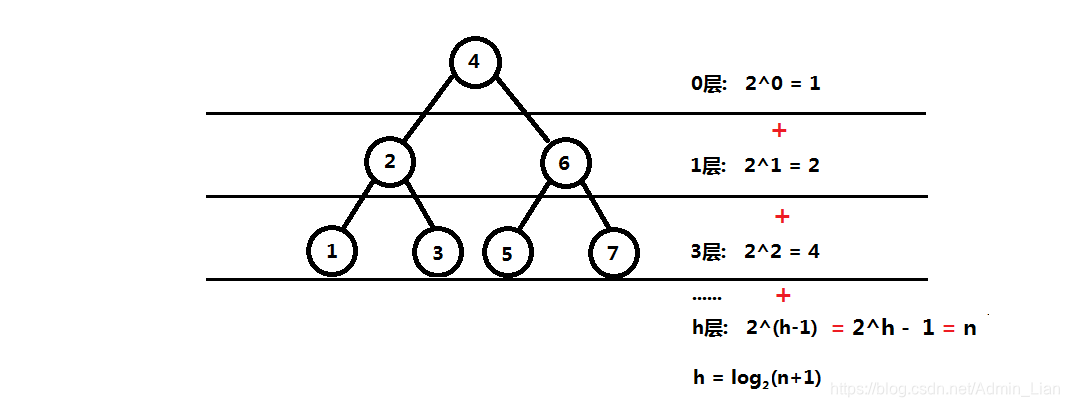
二分搜索树的添加操作, 删除操作, 查询操作的 平均 时间复杂度为 O(logn), 忽略底数2和常数1
