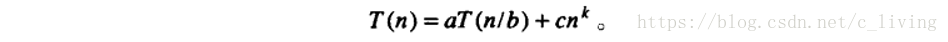对于算法的分析我相信大部分的初学者都是一知半解的。对于时间复杂度我们先介绍简单的概念,简而言之就是找到重复频率最高的语句,并观察该语句随着输入数据个数的增加而增加的速度的规模。比如我们常以:n,n^2,n^3等速度级别来衡量。首先我们来分析比较简单的时间复杂度:
那么我们不得不从最基础的循环来讲起:
for(int i = 0;i < n;i++)
for(int j = 0;j < n;j++)
a++;
a = b+a;
这段代码的时间复杂度显然就是循环中a重复的次数,因为循环的外面的语句在随着n趋近于(我们这样假定)无穷大的时候是可以忽略不计的。所以就是n^2的时间复杂度,记为O(n^2);然后我们再来分析一个深入一步的时间复杂度:
while(i < n)
i = i * 2;这段代码就稍微比上一段难以分析一点,为什么呢?因为这次循环中的执行次数是没有上面那段代码那么直接的,可以一眼看出来。但是我们只要稍微算一下就知道,在经过[log2n](取高斯函数)次数后就会执行完毕,那么时间复杂度自然就是O(log2n)。那么接下来我们再来分析一个再深入一点的例子:
int fact(int n){
if (n<=l) return 1;
return n*fact(n-1);
}这段代码的作用是计算阶乘,但是是使用的递归的设计方法,所以是比较难以看出来的,但是我们透过现象看本质可以发现,这其实还是计算阶乘,那么计算的时候必须要执行的语句那就一目了然了,每次递归执行一下if语句,然后是阶乘,所以是O(n);那么这就是大概比较简单的几种类型,典型的就是直接数循环的重数。
但是事实并不是那么的尽如人意,还有一些比较复杂的时间复杂度的计算,如果我们要理解下面的内容,我们是有必要从时间复杂度的定义入手了。首先我们应该了解一下符号O,前面我们一直都直接记录为O(n)等,并不知道O代表的是什么,那么现在我要告诉你的就是,这里的O表示存在一个关于输入数据规模N的函数f(n)有:
该算法的时间复杂度(n) <= c*f(n),其中只要存在整数C即可,那么我们就可以说算法的时间复杂度上限是O(f(n)),也就是说其实O(n)之类的表示是表示的一个算法的时间复杂度的上限,也就是一个算法最糟糕的情况下所花费的时间,那么同样的对应有:
该算法的时间复杂度(n) >= c*f(n),其中只要存在整数C即可,那么我们就可以说算法的时间复杂度下限是
但是我们平常的讨论一般只对O进行计算,因为下限并不是那么好计算,因为寻找下限是要找出一个算法优于当前的算法,这往往是难以办到的。
介绍玩基本的概念我们下面就要介绍最难的一种时间复杂度的计算,那就是递归算法的时间复杂度的计算:
方法一:公式法(主定理法):
这个公式一般是由分治算法得来的,意义就是将问题T(n)划分为a个T(n/b)的问题来进行计算,然后cn^k表示最后的合并的时间花销。对于该公式给出以下的定理:
下面我们来推导这个公式,因为这样你就很容易记住。我们试着按照递归的思路进行递推式的展开,那么就有:
显然此时只需要讨论这个几何级数就可以得到上面的结论了,注意带入递归的出口的条件。
方法二:猜测法:
该算法是对于给定的递推式给一个自己的猜想,然后进行验证看是否会出现矛盾。比如非常著名的Fibonacci数列:
F(n) = F(n-1) + F(n-2)计算该算法的时间复杂度上限,我们应该如何去猜想呢?首先观察该递推公式,我们可以发现后项是前两项的和,那么我们有理由猜测是F(n) = 2 * F(n-1) = 2 * 2 * F(n-2) = .......=2^(n-1) * F(1),而F(1) = 1;那么我们可以合理的猜测为F(n) = 2 ^ (n-1),然后代入原来的地推公式有:2 ^ n = 2 ^(n-1) + 2 ^ (n-2);但是这个显然是左式远大于右式而O是要寻找一个上限,那么显然是左式该缩小,那么看来2^n是太大了,那么我们继续缩小,那么让底数变成a(a < 2)然后有:
a^n = a ^(n-1) + a^(n-2) 简化为:a^2 = a +1显然可以解得该方程的解为: