本文根据MLaPP第23章,从importance sampling开始梳理,直至导出粒子滤波,并给出相应的范例程序。rejection sampling太简单,就不介绍了。
1. Importance sampling
Importance sampling主要是为了解决 I = E[f] = integral(f(x)*p(x)) 的问题,其中p(x)不能直接抽样,但可以直接计算。
为此,引入可以直接抽样的分布函数q(x),则 I = integral(f(x)*p(x)/q(x)*q(x)) ~= sum(ws'*f(xs))/S,其中xs是根据q(x)的直接抽样,ws' = p(xs)/q(xs),也就是importance weights。
书中这时引入了概率分布归一化因子Zp和Zq,用来推导归一化的ws'(即书中未归一化的ws~,注意书中ws~和ws前后有些混淆,注意甄别)。个人认为并不需要,可以这样推导:1 = integral(p(x)) = integral(p(x)/q(x)*q(x)) ~= sum(ws‘)/S,从而可以得到 sum(ws') ~= S。代入上式,即可得到I ~= sum(ws*f(xs)) 式(23.26),其中ws = ws' / sum(ws')。
2. Sampling importance resampling (SIR)
有了上面的过程,可以理解书中式(23.30),这里面的xs是基于q(x)抽样的,SIR的目的就是把基于q(x)抽样的xs转换成基于p(x)的抽样。这个过程就比较直接了,根据式(23.30),此时的p(x)相当于是一个离散的随机变量,它可能的取值就是xs,对应的概率是ws,对它抽样当然就是按照ws的概率抽样xs了,从而得到(23.34)。
3. Particle filtering(粒子滤波)
上面的重要性抽样(IS)和SIR都是粒子滤波的基础。
粒子滤波要解决的问题,直观理解,可以认为是非线性动态系统(与线性动态系统LDS对应),即状态转移函数、观测函数都可能不是线性的;目标是根据观测到的数据序列y,预测真实数据序列z。
这种情况下,显然已经无法像卡尔曼滤波那样得到解析公式,只能使用抽样,拟合p(z|y),从而获得z的预测。
具体来说,就是:1.先对z(0)抽样,得到一系列抽样值zs(也就是所谓的粒子);选择相应的q(x),进而决定了ws;2.逐级迭代,得到后续各级z(t)的分布抽样(p(z|y)),进而得到z(t)的预测值。迭代公式参见MLaPP第23.5.1中的系列公式,个人认为还是相当清晰的。
上述是所谓粒子滤波的基础算法,其实只用到了重要性采样,并未用到SIR。但是基础算法有个致命的问题,就是degeneracy problem,按照我的理解就是,z(t-1)和z(t)的分布可能很不一样,这样在z(t-1)根据重要性采样出来的zs,在z(t)时可能是很不重要的点了,而对于z(t)重要的点反而没有抽样到,或者即使抽样到,也很少,这时计算精度会变得很糟糕。
那怎么办?MLaPP中给出两种解决方案:1.重采样,就是经过若干迭代,等效抽样数(Seff,式(23.47)、(23.48))小到某个阈值之后,重采样,也就是用到上述的SIR算法了;重采样还有个问题,就是抽样点impoverishment,毕竟重采样使用sample with replacement进行的;2.q(x)选择,也就是选择式(23.52)中的q(x)函数。
这两种解决方案的关系在书中并未写清楚。看网上的程序,应该是同时使用;实际操作中也发现,只使用方案2似乎也不解决问题。
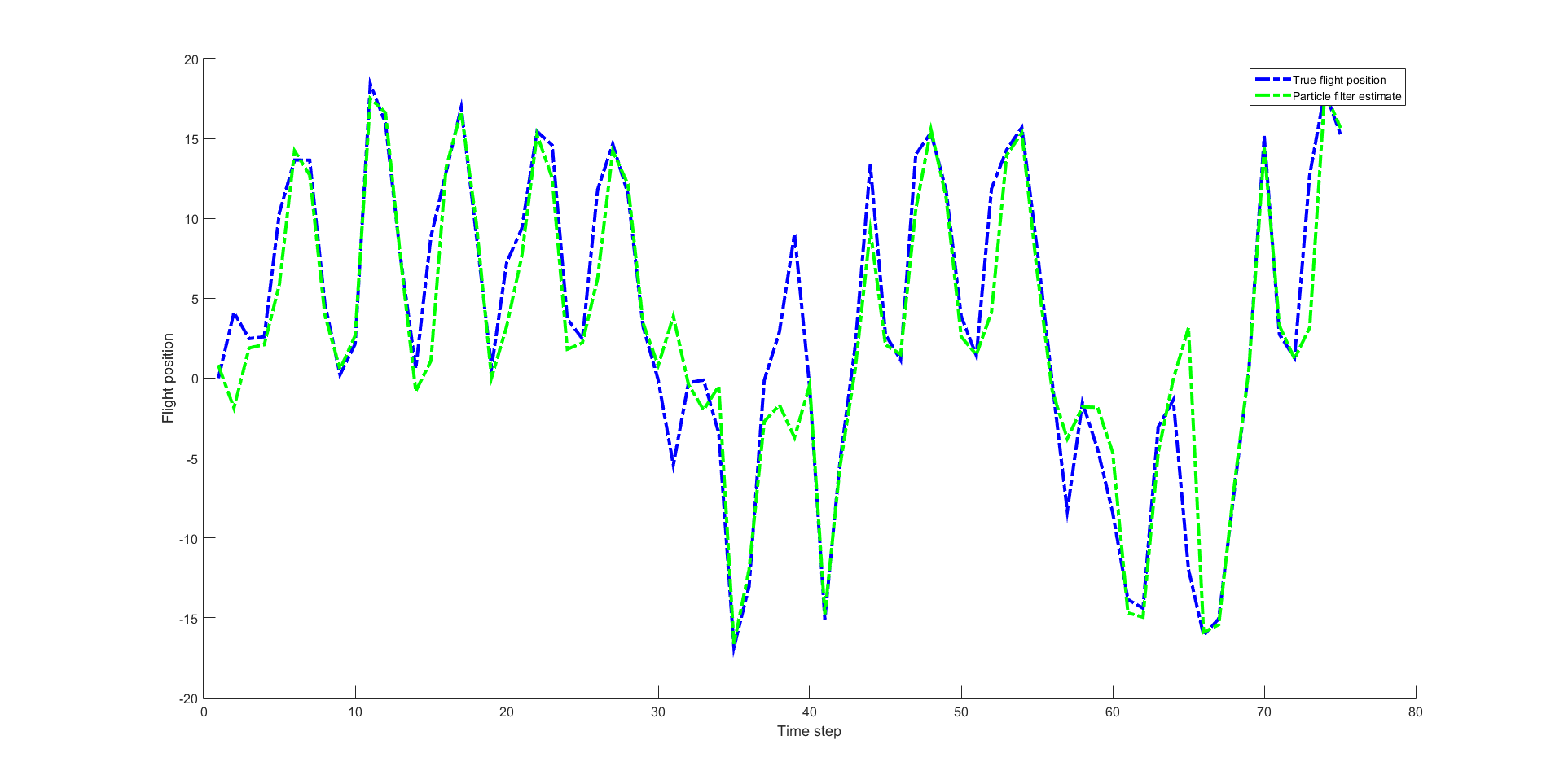
下面给出范例程序,其中粒子滤波部分参考了 http://blog.csdn.net/liujiakuino1/article/details/54343527 中的代码,但进行了调整。输出如下:
代码如下:
%% Monte Carlo Inference (MLaPP, Chapter 23):
% 2017.12.22
% QQ: 50834
% http://blog.csdn.net/foreseerwang
% 1. Importance sampling
% 1.1 Basic idea (MLaPP, 23.4.1)
% 1.2 Unnormalized distributions (MLaPP, 23.4.2)
% 1.3 SIR: Sampling importance resampling (MLaPP, 23.4.4)
%
% 2. Particle filter
% 2.1 Sequential importance sampling
% 2.2 Resampling
% 2.3 Proposal distribution
close all;
clear all;
rng(0);
%% 1. Importance sampling
fprintf('==============================================================\n');
fprintf('Importance sampling (MLaPP, 23.4)\n');
% 各种函数定义
fun_px_pdf = @(x)(normpdf(x, 5, 0.4)*0.7+normpdf(x, -7, 2)*0.3);
fun_qx_smp = @(x)(randn(x,1)*5);
fun_qx_pdf = @(x)(normpdf(x, 0, 5));
fun_fx = @(x)(1./(1+exp(-x)));
% 初始化
S = 10000; % 抽样数量(粒子数目)
N = 1; % 重复次数
S_SIR = round(S/10); % SIR数量,MLaPP (23.34)中的S',远小于S
% f(x)相对于p(x)的理论均值
dx = 0.1;
x = -20:dx:20;
px = fun_px_pdf(x);
fx = fun_fx(x);
E_f = sum(fx.*px)*dx;
fprintf('Expectation of f(x) is: %5.3f\n', E_f);
figure; scatter(x,px); hold on; scatter(x,fx);
legend('p(x)', 'f(x)');
set(gca,'FontSize',12); set(gcf,'Color','White');
% 1.1和1.2,对应MLaPP 23.4.1和23.4.2
E_f1 = 0;
E_f2 = 0;
for ii = 1:N,
% 引入已知分布q(x),其核心思想是要用q(x)抽样
% 本例中q(x) = norm(x|0,5)
x_samp = fun_qx_smp(S);
px_samp = fun_px_pdf(x_samp);
qx_samp = fun_qx_pdf(x_samp);
% Basic idea
ws = px_samp./qx_samp;
fx_samp = fun_fx(x_samp);
E_f1 = E_f1*(ii-1)/ii+sum(ws.*fx_samp)/S/ii; % MLaPP (23.20)
% Handling unnormalized distributions
ws2 = ws/sum(ws); % MLaPP (23.27)
E_f2 = E_f2*(ii-1)/ii+sum(ws2.*fx_samp)/ii; % MLaPP (23.26)
end;
% 这两种方法的计算结果应该一样
fprintf('Expectation of f(x) using IS (basic idea) is: %5.3f\n', E_f1);
fprintf('Expectation of f(x) using IS (normalized) is: %5.3f\n', E_f2);
% SIR: Sampling importance resampling,对应MLaPP 23.4.4
x_SIR = zeros(1,S_SIR);
p_SIR = zeros(1,S_SIR);
for ii = 1 : S_SIR,
tmp_idx = find(rand <= cumsum(ws2),1);
x_SIR(ii) = x_samp(tmp_idx);
p_SIR(ii) = ws2(tmp_idx);
end
p_SIR = p_SIR/sum(p_SIR);
figure( 'name', 'SIR: Sampling importance resampling');
set(gca,'FontSize',12); set(gcf,'Color','White');
subplot(1,2,1);
hist(x_SIR,100);
xlabel('x'); ylabel('p(x)');
title('Resampling Results');
subplot(1,2,2);
scatter(x_SIR, p_SIR);
xlabel('x'); ylabel('p(x)');
title('p(x) after resampling');
%% 2. Particle filter
% 针对SSM (State space models),z为隐变量,y为观测量
% 状态转移函数:z(k) = f(z(k-1)) + v
% 状态观测函数:y(k) = h(z(k)) + n
% 已知:y(1:k)
% 目标:计算p(z(k)|y(1:k)),进而求得z的估计值
fprintf('\n==============================================================\n');
fprintf('Particle filtering (MLaPP, 23.5)\n');
clear all;
% function definition
% Ref. to: http://blog.csdn.net/liujiakuino1/article/details/54343527
% 在真实的应用中,f和h应该是知道的,但v、n未知
fun_f = @(z,t)(0.5*z + 25*z./(1 + z.^2) + 8*cos(1.2*(t-1)));
fun_v = @(N,mu,sig)(randn(1,N)*sig+mu);
fun_h = @(z)(z.^2/20);
fun_n = @(N,mu,sig)(randn(1,N)*sig+mu);
fun_p = @(x,mu,sig)(normpdf(x,mu,sig));
% 参数初始化
T = 75; % 共进行75次迭代
S = 1000; % 粒子数,越大效果越好,计算量也越大
% 真实高斯误差参数
v_mu = 0; v_sig = 1;
n_mu = 0; n_sig = 1;
% 预测高斯误差参数
qv_mu = 0; qv_sig = 2;
qn_mu = 0; qn_sig = 2;
% 生成并显示状态序列z和观测序列y
z = zeros(1,T);
z(1) = 0.1;
for ii = 2:T,
z(ii) = fun_f(z(ii-1),ii)+fun_v(1,v_mu,v_sig);
end;
y = fun_h(z) + fun_n(T,n_mu,n_sig);
% 后面除了打印显示,不应该再用到z和v/n的均值和方差
zs = fun_v(S, y(1), qv_sig); % 粒子
z_est = zeros(size(z));
z_est(1) = mean(zs); % 真实位置估计
for ii = 2:T,
zs_new = fun_f(zs,ii)+fun_v(S,v_mu,qv_sig);
ys_new = fun_h(zs_new);
% MLaPP (23.37),重采样之后,ws相等,因此不再*ws(t-1)
ws = fun_p(y(ii),ys_new,qn_sig);
ws = ws/sum(ws); % MLaPP (23.38)
for i = 1 : S
zs(i) = zs_new(find(rand <= cumsum(ws),1)); % 根据ws重采样
end
% 重采样之后,各zs的权重相等了,因此期望值直接取均值即可
z_est(ii) = mean(zs);
end;
figure( 'name', 'Particle Filtering Demo'); hold on;
plot(z,'-.b','linewidth',3); plot(z_est, '-.g','linewidth',3);
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('Time step'); ylabel('Flight position');
legend('True flight position', 'Particle filter estimate');