快速傅里叶变换学习记录——Fast Fourier Transformation

序言

掌声鼓励，本蒟蒻终于学会FFT啦！
死磕了接近5天的FFT，中途断断续续，请教了所谓的“数论讲师”葛某。
他居然告诉我：
他不会！！！
他不会！！！
他不会！！！
他不会！！！
他不会！！！
他不会！！！

前排膜拜dalao

如果觉得本人蒟蒻的，勿喷，可以看这两位dalao的Blog：
Mikcoo
Picks

前排预警：这篇Blog有很多公式！！！

预备知识

数论dalao可以直接跳过了……

多项式

形如$A\left(x\right)=a_0+a_1x+a_2x^2+\cdots+a_nx^n$的称为多项式。
$a_0,a_1,\cdots,a_n$称为多项式的系数。
$x$为不定元，不表达任何确定值。
不定元$x$在多项式中最大的次数称为多项式的次数。

多项式的系数表达法

多项式的系数表示为$n+1$维向量$\vec a=\left(a_0,a_1,\cdots,a_n\right)$。
简单理解为一个数组就好……数学家总是喜欢搞些奇奇怪怪的东西。

多项式的点值表示法

已知对于一元$n$次方程可以用$n+1$个点的坐标表示。（理由自证）
多项式的点值表示为$\{(x_i,A(x_i)):0\leq i\leq n\}$。
还可用点值向量$\vec y=(A(x_0),A(x_1),\cdots,A(x_n))$

复数

形如$a+bi$的数称为复数，其中$a,b$为实数，$i$为虚数单位，满足$i^2=-1$’

单位根

$n$次单位根$\omega_n$为满足$\omega_n^n=1$的复数，共有$n$个，均匀的分布在复平面的单位圆上，将单位圆$n$等分。
所以$n$次单位根的算术表示为$\omega_n=e^{\frac{2\pi i}{n}}$。

多项式乘法

给定两个多项式$A(x),B(x)$，求$C(x)=A(x)B(x)$

系数表示法下的运算

$\because C(x)=\sum\limits_{i=1}^{2n}c^ix^i$
$\therefore C(x)=\sum\limits_{j+k=i,0\leq j,k\leq n}a_jb_kx^i$
易证时间复杂度为$O(n^2)$

点值表示法下的运算

$\because C(x)=A(x)B(x)$
$\therefore C(x_i)=A(x_i)B(x_i)$
$\therefore C(x)$的点值表示为$\{(x_i,A(x_i)B(x_i)):1\leq i\leq n\}$
易证时间复杂度为$O(n)$

Fast Fourier Transformation

FFT在竞赛中一般用于加速多项式乘法运算。
现在引入FFT（Fast Fourier Transformation）。
我们观察到对于以上两种运算，点值表示法下的运算明显优于系数表示法下的运算，考虑将运算过程转移到点值表示法下。
使用暴力强行将系数表示法转换为点值表示法的时间复杂度是$O(n^2)$，这里不再做讨论。

FFT算法流程

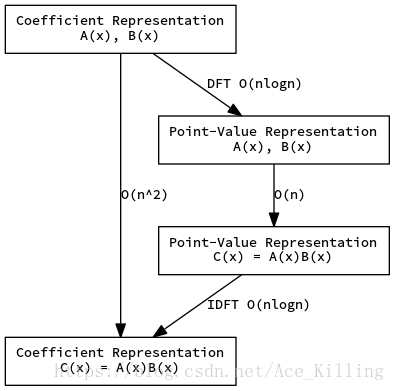
英文看的辛不辛苦啊，我就不翻译。（手动滑稽）

Discrete Fourier Transform

DFT的目的是将系数向量$\vec a$转换为点值向量$\vec y$。
将$n$个相异实数$x_0,x_1,\cdots,x_{n-1}$代入多项式。
$\therefore A(x_k)=\sum\limits_{i=0}^{n-1}a_ix_k^i,(0\leq k\leq n-1)$
$\therefore A(x)$的点值表示为$\{(x_k,A(x_k)):0\leq k\leq n-1\}$
$\therefore$点值向量$\vec y=(A(x_0),A(x_1),\cdots,A(x_{n-1}))$
点值向量$\vec y$称为系数向量$\vec a$的离散傅里叶变换（Discrete Fourier Transform），记作$\vec y=DFT_n(\vec a)$
易证上述做法时间复杂度为$O(n^2)$

Cooley-Tukey算法（蝶形算法）

以下摘自Wiki：

库利－图基快速傅里叶变换算法（Cooley-Tukey算法）[1]是最常见的快速傅里叶变换算法。这一方法以分治法为策略递归地将长度为N = N1N2的DFT分解为长度分别为N1和N2的两个较短序列的DFT，以及与旋转因子的复数乘法。这种方法以及FFT的基本思路在1965年J. W. Cooley和J. W. Tukey合作发表An algorithm for the machine calculation of complex Fourier series之后开始为人所知。但后来发现，实际上这两位作者只是重新发明了高斯在1805年就已经提出的算法（此算法在历史上数次以各种形式被再次提出）。
库利－图基算法最有名的应用，是将序列长为N的DFT分割为两个长为N/2的子序列的DFT，因此这一应用只适用于序列长度为2的幂的DFT计算，即基2-FFT。实际上，如同高斯和库利与图基都指出的那样，库利－图基算法也可以用于序列长度N为任意因数分解形式的DFT，即混合基FFT，而且还可以应用于其他诸如分裂基FFT等变种。尽管库利－图基算法的基本思路是采用递归的方法进行计算，大多数传统的算法实现都将显示的递归算法改写为非递归的形式。另外，因为库利－图基算法是将DFT分解为较小长度的多个DFT，因此它可以同任一种其他的DFT算法联合使用。

从中我们注意到一句话：“……因此这一应用只适用于序列长度为$2$的幂的DFT计算……”。
所以，为了计算的方便，我们将$n-1$位多项式$A(x)=\sum\limits_{i=0}^{n}a_ix^i$补位至2的幂。（$n=2^n,m\in\mathbb {Z}$，高位补为$0$）
将$n$个单位根$\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$代入多项式。
$\therefore A\left(\omega_n^k\right)=\sum\limits_{i=0}^{n-1}a_i(\omega_n^k)^i,(0\leq k\leq n-1)$
$\therefore A(x)$的点值表示为$\{(\omega_n^k,A(\omega_n^k)):0\leq k\leq n-1\}$
$\therefore$点值向量$\vec y=(A(\omega_n^0),A(\omega_n^1),\cdots,A(\omega_n^{n-1}))$
现在Cooley-Tukey算法将每一项系数按指数奇偶分类，以此将系数减半：
$\begin{equation} \begin{split} A(\omega_n^k)&=\sum\limits_{i=0}^{n-1}a_i\omega_n^{ki}\\ & = \sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i}\omega_n^{2ki}+\omega_n^k\sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i+1}\omega_n^{2ki}\\ \end{split} \end{equation}$
现在我们考虑如何将代入的值也减半：
因为：
$\begin{equation} \begin{split} \omega_n^2&=\left(e^{\frac{2\pi i}{n}}\right)^2\\ &=e^{\frac{4\pi i}{n}}\\ &=e^{\frac{2\pi i}{n/2}}\\ &=\omega_{\frac{n}{2}} \end{split} \end{equation}$
且当$k<\frac{n}{2}$时
$\begin{equation} \begin{split} \omega_n^{k+\frac{n}{2}}&=\omega_n^{\frac{n}{2}}\cdot\omega_n^k\\ &=-1\cdot\omega_n^k\\ &=-\omega_n^k \end{split} \end{equation}$
所以：
当$k<\frac{n}{2}$时
$\begin{equation} \begin{split} A(\omega_n^k)& = \sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i}\omega_n^{2ki}+\omega_n^k\sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i+1}\omega_n^{2ki}\\ &=\sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i}\omega_{\frac{n}{2}}^{ki}+\omega_n^k\sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i+1}\omega_{\frac{n}{2}}^{ki}\\ A(\omega_n^{\frac{n}{2}+k})&=\sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i}\omega_{\frac{n}{2}}^{ki}+\omega_n^{\frac{n}{2}+k}\sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i+1}\omega_{\frac{n}{2}}^{ki}\\ &=\sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i}\omega_{\frac{n}{2}}^{ki}-\omega_n^k\sum\limits_{i=1}^{\frac{n}{2}-1}a_{2i+1}\omega_{\frac{n}{2}}^{ki}\\ \end{split} \end{equation}$
需要代入的值有$\omega_{\frac{n}{2}}^0,\omega_{\frac{n}{2}}^1,\cdots,\omega_{\frac{n}{2}}^{\frac{n}{2}-1}$，问题转换为两个折半的子问题，可通过递归或迭代实现。
易证时间复杂度为$O(n\log n)$。
至此，通过Cooley-Tukey算法，我们将DFT的时间复杂度降为$O(n\log n)$。

Inverse Discrete Fourier Transform

IDFT的目的是将点值向量$\vec y$转换为系数向量$\vec a$
IDFT就相当于把DFT过程中的$\omega_n^k$换成$\omega_n^{-k}$，然后做一次DFT，之后结果除以$n$就可以了。
这里只给出结论，用兴趣的同学可以自行研究。（你就是懒得写）

总结

对于多项式的运算（高精度预算），使用FFT可以实现十分好的时空复杂度优化。