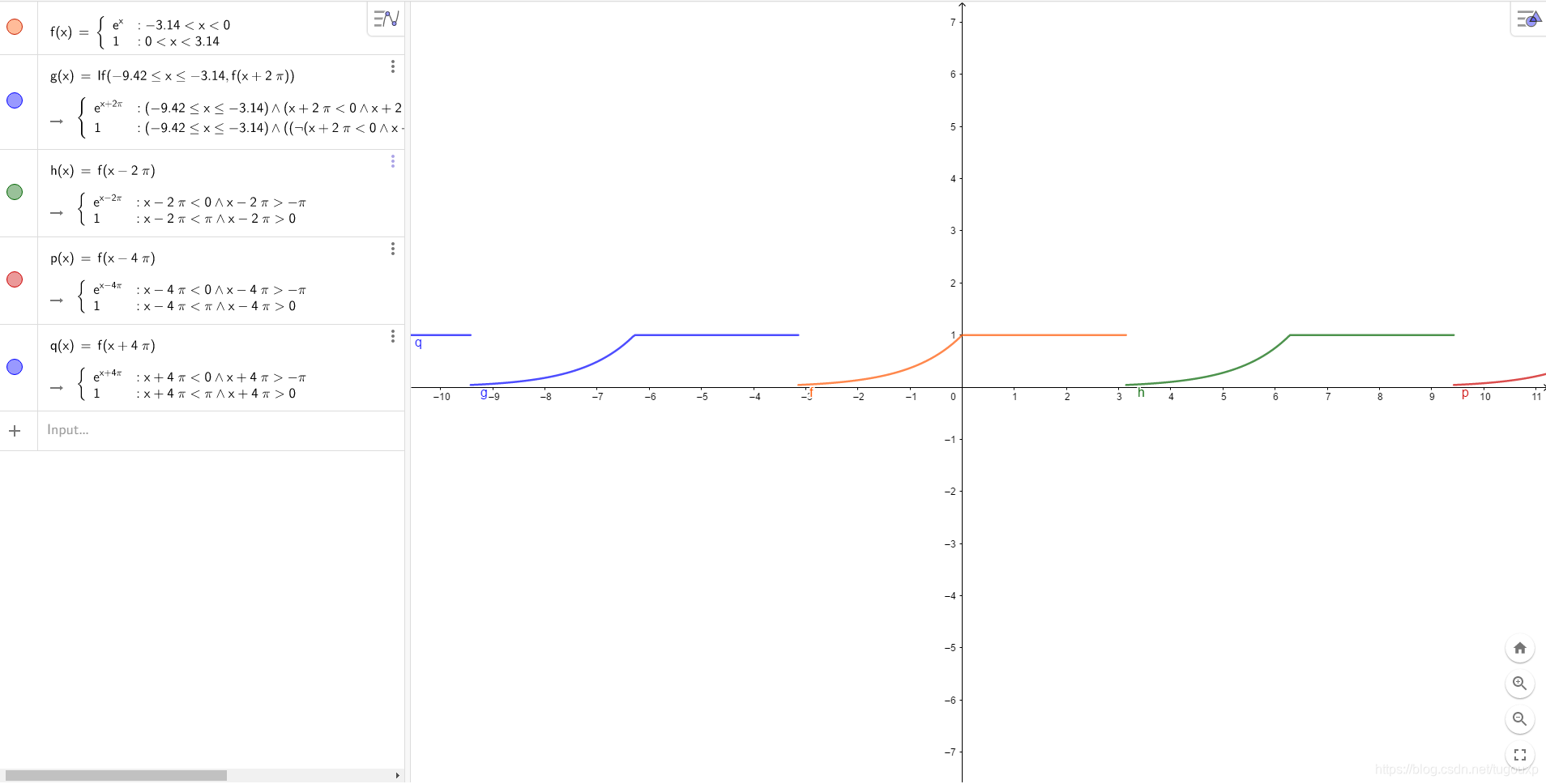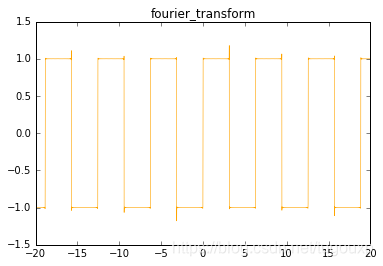
如同泰勒级数一样,Fourier级数是一种特殊形式的函数展开,一个函数按照泰勒级数展开时,基底函数取
而一个函数按傅里叶级数展开时,基底函数取
它们构成无穷维的空间,这些无穷维空间的表示多是完备的,也就是缺少任何一个都不可以。最常遇到的函数在它的定义域内每一点都可以展开成幂级数,而傅里叶展开则需要一些条件。
与泰勒级数不同的是,在傅里叶级数中,任意两个不同的基底函数在上是正交的.也就是:

这里,基底函数的正交性对一个函数的傅里叶展开是至关重要的,傅里叶级数是一种很自然的函数展开形式,不但能够解决某些数学上的经典问题,而且是描述许多重要物理现象的基础,如力学,声学,电子学以及信号分析,控制科学等.
一个傅里叶级数在一般情况下表示为:
其中,和
是展开系数.假定一个周期为
的函数
能按上式展开,之所以假定周期为是为了计算方便,因为周期为
的函数,角速度为:
这样,展开后的各次谐波可以写成
的形式.当然定义周期非也可以,只是推到过程中函数形式上会复杂一些,这里为了方便计算,定义周期为
.
所以,傅里叶级数可以看成一些列周期为
的三角波的叠加。
即便, 最终积分的时候,根据积化和差公式,得到包含
,
,
,
的项,它们的角频率都是一次谐波的整数倍,也就是说,周期都可以被一次谐波整除,而积分范围是一次谐波的一个周期范围,必定包含整数个高次谐波的波形,而三角波再周期范围内积分为0,所以,积分结果也必定为0.
现在计算其中的展开系数.
对上式两边在范围进行积分,并利用正交性:
所以:
所以是函数
在
区间的平均值,为了计算系数
,按照同样的套路,对两边同乘以
,然后在
范围积分,并利用正交性,得到:
所以:
类似,对前式两边同乘以,积分后得到:
Notes: 上面计算过程的积分范围是,其实也可以选择
,计算结果系数表达式不变,只是将积分范围变为
,事实上,由于被积分的函数是以
为周期的,积分范围可以选择任意一个宽度为
的区间.
傅里叶变换的本质是内积,内积的本质是投影,三角函数的特殊性在于,它是一个完备的正交函数集,不同频率的三角函数之间的内积为0,也就是垂直,正交,或者毫不相关,只有频率相同的三角函数,内积才不是0(很显然,自身到自身的投影,长度一定不为0, 除非自身就是0).从这个角度看,我们求得的傅里叶系数只是再不同的函数上的投影坐标。
综上,得到傅里叶系数:
假如被积函数有周期,则积分区间可以用任意一个宽度为
的区间代替,例如
.,因为无论区间怎样取,周期内积分必定相等.
从纯数学的角度讲,上面的过程是使用三角函数逼近周期函数的过程,如果在频率增加时,fourier系数快速收敛为0,则信号表现是光滑的,如果在频率较大的时候,有一些系数仍然无法收敛,则图形会变成有高频噪声的情况,可以使用低通滤波对频率进行过滤,得到低频部分.
法国数学家傅里叶在提出傅里叶级数时认为,任何一个周期信号都可以展开成傅里叶级数,后来发现还要加上一些条件,不过这些条件非常的弱,之后经过进一步补充,只有在满足狄利克雷条件时,周期信号才能够被展开成傅里叶级数。其中,狄利克雷条件的定义如下:
- 在一周期内,连续或只有有限个第一类间断点.(如果
是函数
的间断点,且左极限及右极限都存在,满足这些条件的间断点成为第一类间断点).
- 在一周期内,极大值和极小值的数目应是有限个,翻译过来就是,分段单调,单调区间的个数有限.
- 在一周期内,信号是绝对可积的。
这三个条件是充分条件,但不是必要条件,也就是说,存在一些函数有傅里叶展开,但是却不一定满足上面这三条,但是对于满足上面三条的函数,一定可以进行傅里叶级数展开.
关于间断点的分类,见下图:

收敛情况,在的连续点,傅里叶级数收敛于:
但是在的间断点,收敛于:
其中和
是
在
处的左极限和右极限,这里的含义是,如果将函数按照傅里叶级数展开,这个傅里叶级数再原函数的一个连续点收敛于对应连续点的值,但是在原函数的一个间断点,则收敛于这个间断点左右极限的算数平均值.
这也侧面反应,左右极限存在是傅里叶变换可以进行的必要条件.
另外,根据条件1和条件3,也可以得出, 随着系数增大,逐渐趋于0的事实,这也说明傅里叶变换后,高频分量能量趋近于零,可以忽略。
现在我们证明一下:
根据条件1和3,f(x)满足绝对可积,只有有限个第一类间断点,则可以得到f(x)函数在周期内一定有界,包括上界和下界,所以下式一定成立:
一定成立
所以
后面还会看到傅里叶级数的复指数形式也有一个系数,它的系数表示为:
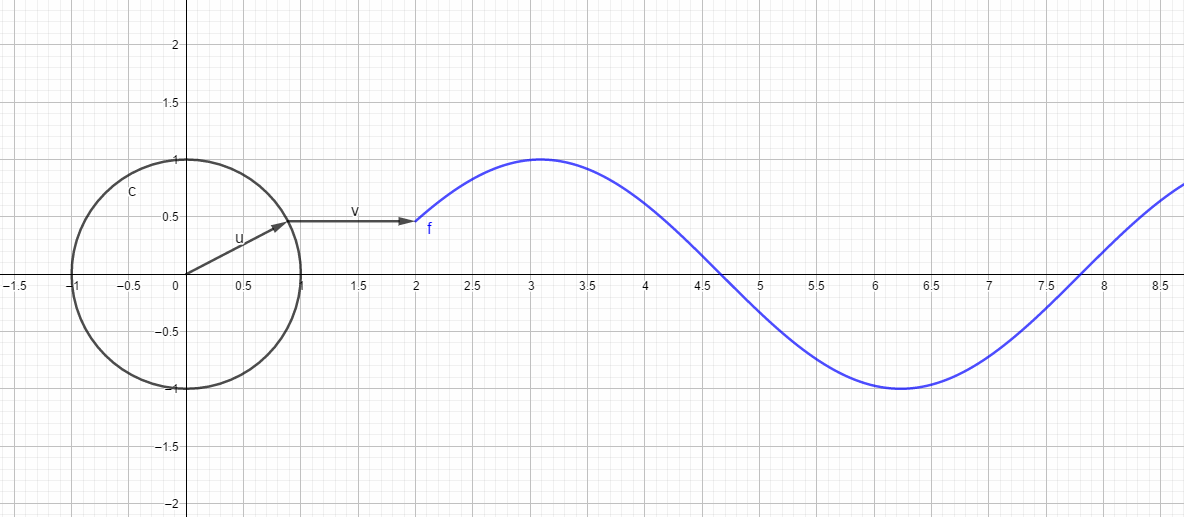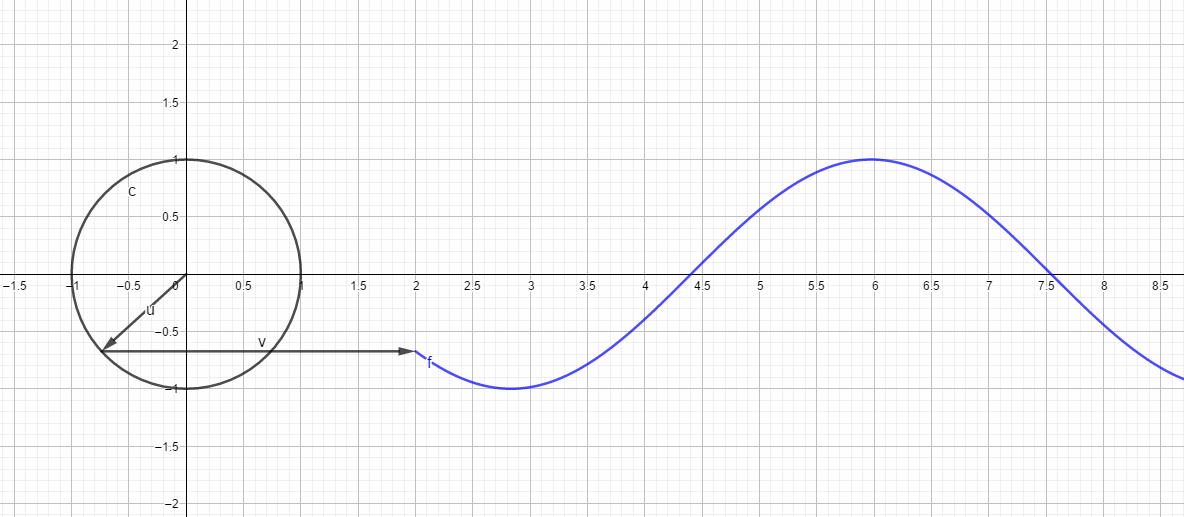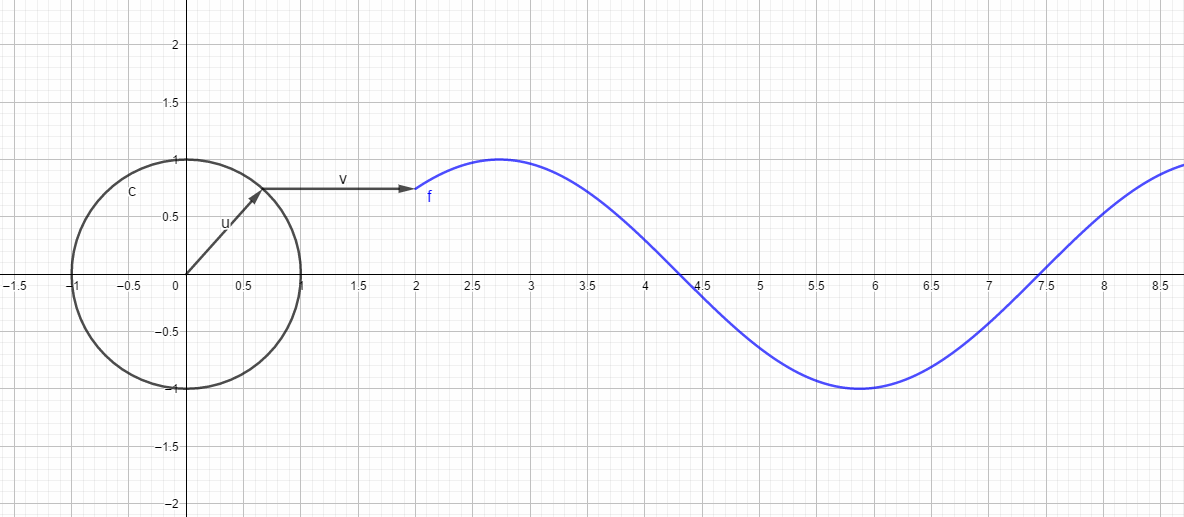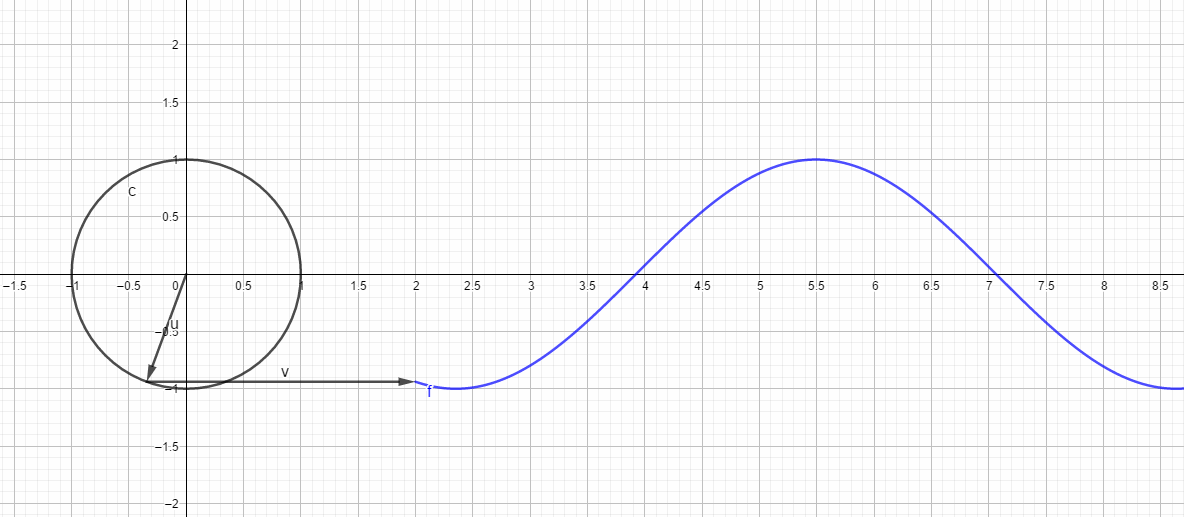
模表示单位圆的半径幅度:
可以看到,随着,傅里叶变换复指数形式的系数表示环绕圆半径也是逐渐减小的。
所以, 随着系数增大,绝对值逐渐趋于0的判断成立,几何化表示就是,频域圆圈套圆圈,后面的圆圈越来越小。
傅里叶级数的复数形式推导:
根据欧拉公式:
所以
所以:
由于
所以
注意这里是而不是
,所以固定的是上式的结论.
所以:
所以:
这里做一下变量代换,用表示
,用
表示
,其中
也就是新的公式里面的
所以,上面的式子化为:
对于复数代数表达和自然指数表达之间的联系,做如下推导:
如下图:

所以:
其中,
所以,最终傅里叶级数变换和反变换为:
前面说的三角函数是一组正交函数,实际上,也是一组正交函数,并且是完备的,定义为:
上式的一居室柯西积分定理,解析函数沿着任意封闭曲线(内部不包括奇点)的积分值为0
对于傅里叶积分的形式,是不是很像?
实际上,傅里叶级数当时的极限就是傅里叶积分。
区别就在于因子放在哪里,实际上这个差别是有原因的,这里由于假定周期是
,所以因子实际上是
.,傅里叶变换的时候,
,
,这样会导致幅度谱趋近于0,很难画出来表示不同频率分量的强度差异。这样,将
乘以
,则转化为频率密度谱,也就是在连续频率情况下,单位频率内,有多少“幅度”,这就像是算单位体积内物体的质量一样,这样,傅里叶级数就成了傅里叶变换。
简单应用,对于函数:
其复指数形式的傅里叶变换是:
所以:
,其余都为0;
所以:
所以:
对于方波来说:
对于方波,后面有求得
而且:
所以,上面两个方法推推导出了同样的结果.
可以类比连续情况下的fourier 变换:
下面的公式来源于数学物理方法,本质是周期无限大时候的fourier级数.
所以,自然而然,中括号的内容独立出来,推导出傅里叶积分形式:
所以:
可见,正向推导和反向推到都成功了。
根据复数域公式,傅里叶变换可以看成是一个个的角频率不同的圆()的运动的叠加,当n>0时,是逆时针旋转的圆,当n<0时,是顺时针旋转的圆,n==0的时候,表示直流平均分量,不旋转。 不管旋转方向是什么,同意时刻它们的实部投影是时域上的值,虚部投影是0.(上面的式子可以看到大于零和小于零情况下,相同角频率的两个圆它们的相位相反,而角频率相同的情况下,任何时刻互为共轭,虚部矢量和为0,所以只有实世界的分量,也就是时域分量).
1.函数在一个周期内的解析式为:
周期函数下图所示:
所以:
所以:
同理:
所以:
所以
所以
综合上面的推导,得出傅里叶系数分别为:
octave计算各次的系数分别为:
得到包括六次谐波的函数表达式为:
其图形是下图,可以看到,基本上与原函数重合,这也说明上面的积分过程是正确的。
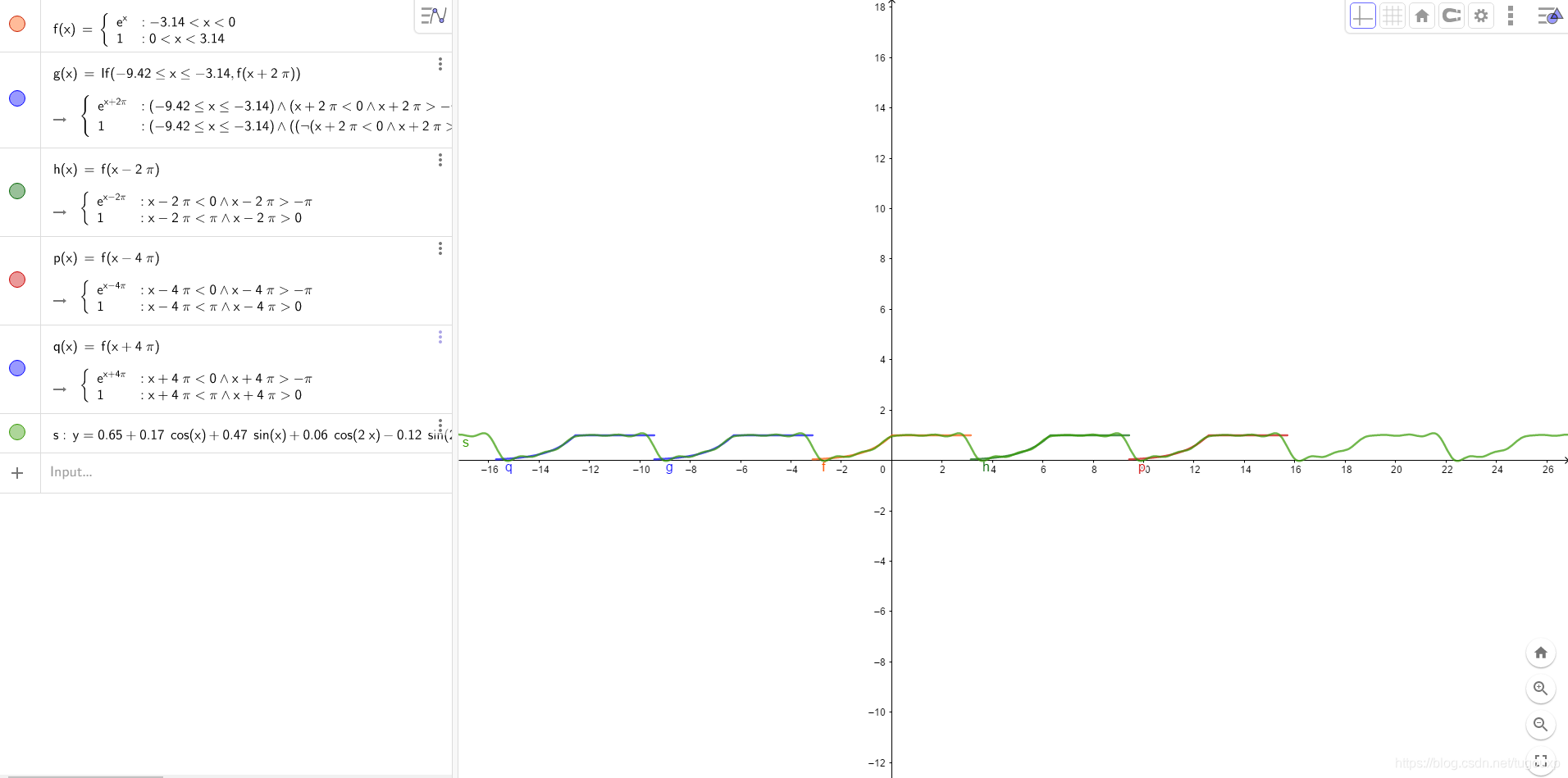
octave计算过程:
 \frac{2}{n\pi}(1-cos(n\pi))
\frac{2}{n\pi}(1-cos(n\pi))
下面用python绘制一幅精确点的图形,下面的图形包含10000个谐波,可以看到,已经非常逼近原函数图形了。
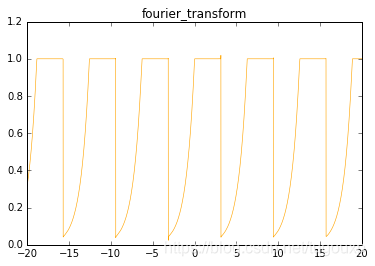
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = (1-exp(-pi))/(2*pi)+1/2
s=a0
for n in range(1,10000,1):
s0 = ((1-(-1)**n*exp(-pi))/(pi*(1+n**2))*cos(n*x)+((n*exp(-pi)*(-1)**n-n)/(pi*(1+n**2))+((-1)**(n+1)+1)/(n*pi))*sin(n*x))
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()
2.方波:
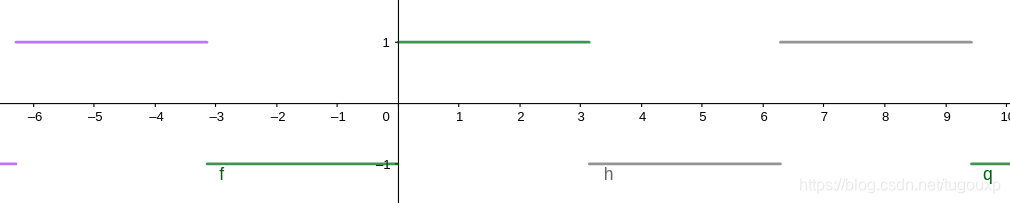
所以:
所以:
geogebra函数图形:
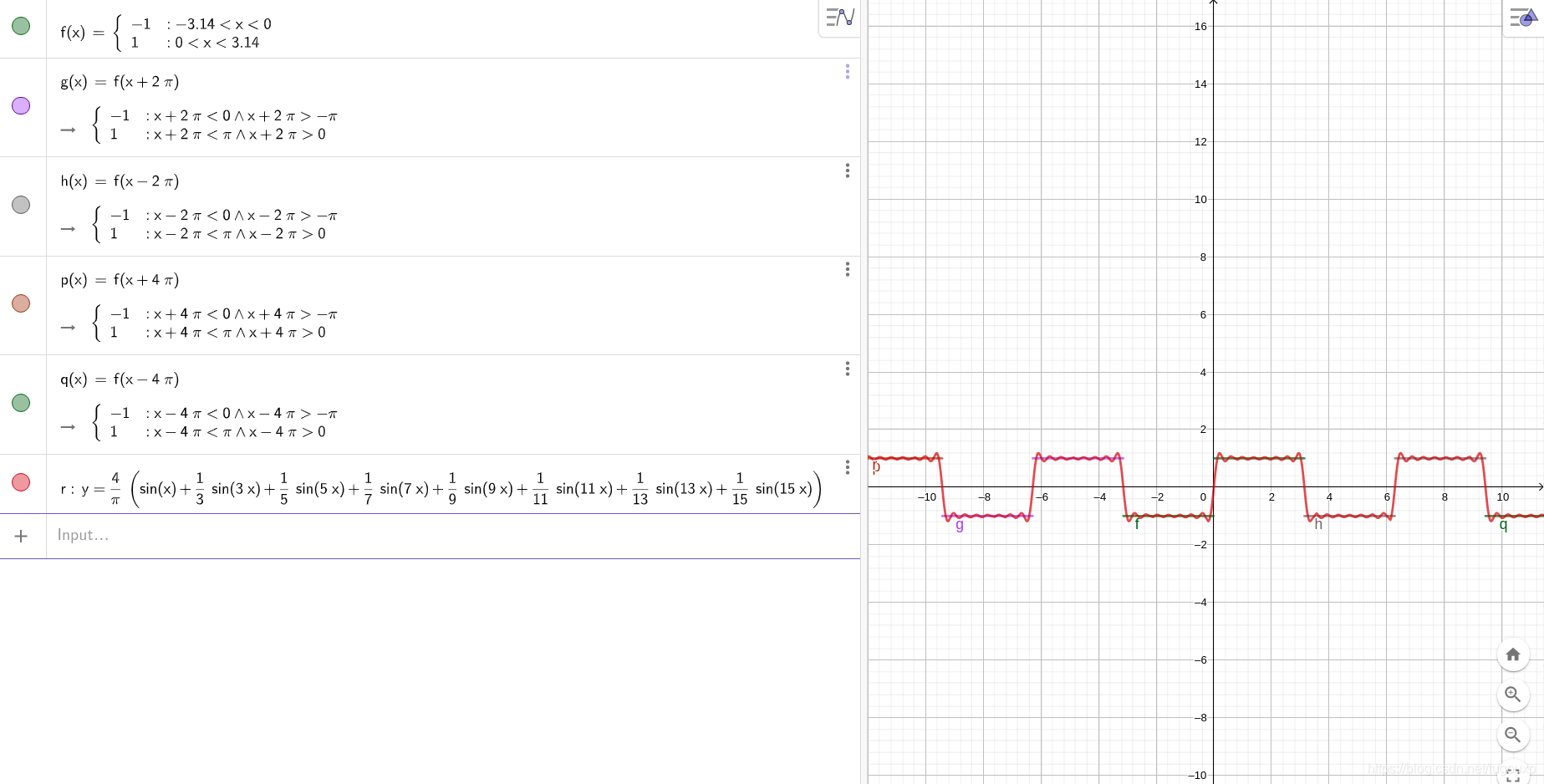
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = 0
s=a0
for n in range(0,1000,1):
s0 = 4/((2*n+1)*pi)*sin((2*n+1)*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()得到如下图像:
3.另一类型的方波

所以
所以:
对比前图,这里的表达式表示沿着横轴左移角度,和前图的解析式形式完全一致.
geogebra验证:
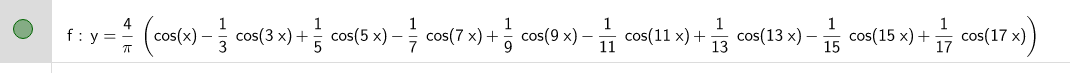

n=17次的谐波是上图的样子.
python验证:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = 0
s=a0
for n in range(0,100,1):
s0 = ((-1)**n*4)/((2*n+1)*pi)*cos((2*n+1)*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()python绘制的图像:
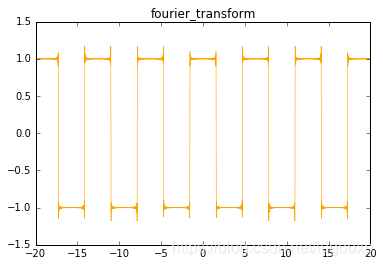
函数4:
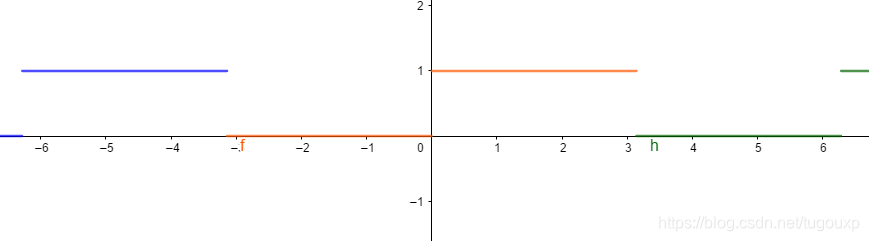
所以:
geogebra图像为:
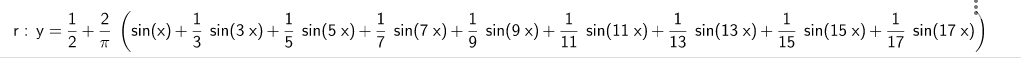

python图像:
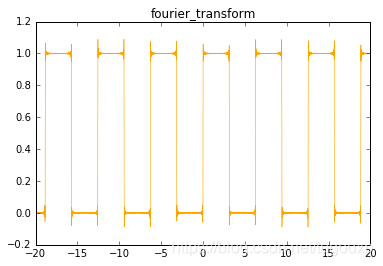
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = 1/2
s=a0
for n in range(0,100,1):
s0 = 2/(pi*(2*n+1))*sin((2*n+1)*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()函数5:
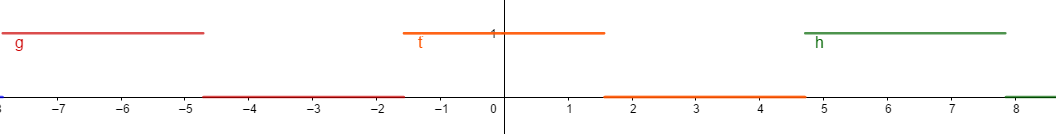
geogebra图形:yu
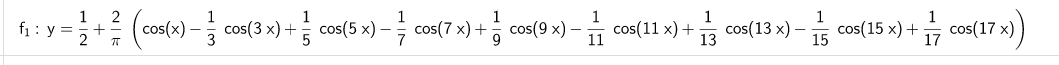

python图形:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = 1/2
s=a0
for n in range(0,100,1):
s0 = ((-1)**n*2)/((2*n+1)*pi)*cos((2*n+1)*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()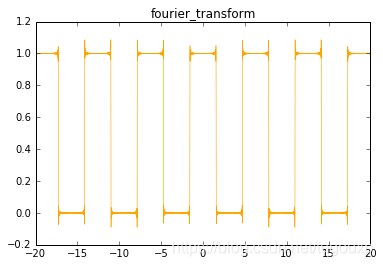
锯齿函数的傅里叶变换:
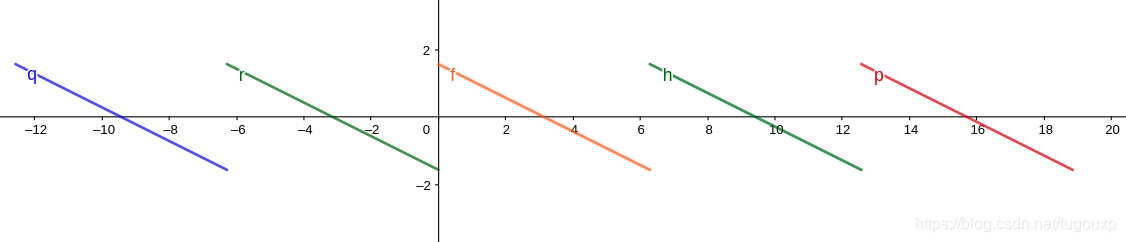
于是:
geogebra图形为:
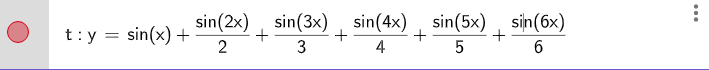
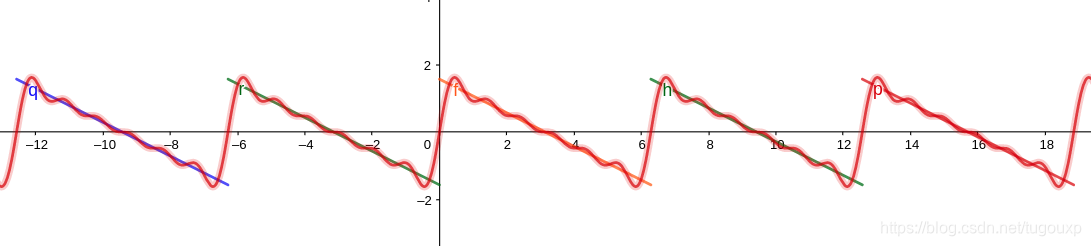
python图形为:
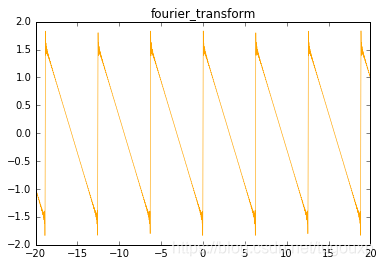
验证,在,收敛于
但是在连续点,收敛于级数
python绘图代码为:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = 0
s=a0
for n in range(1,100,1):
s0 = sin(n*x)/n
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()函数:
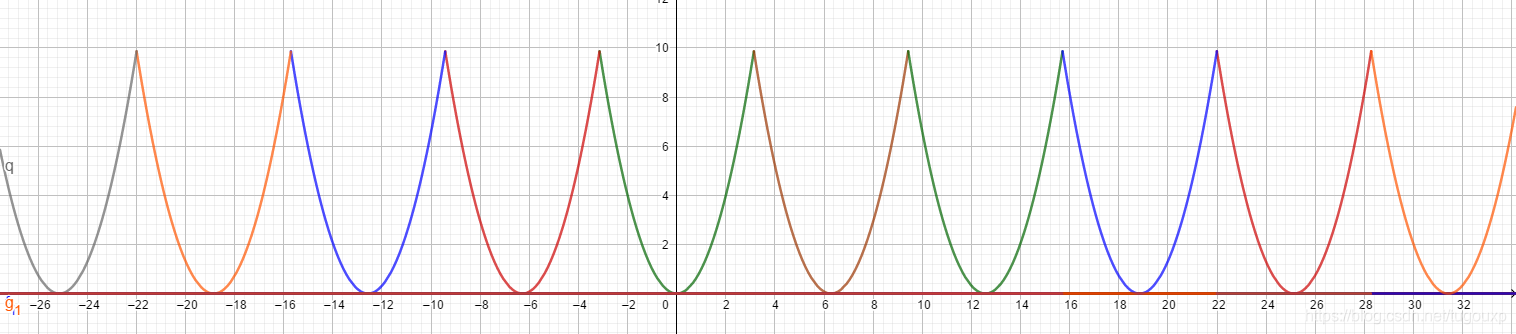
\
python绘图:
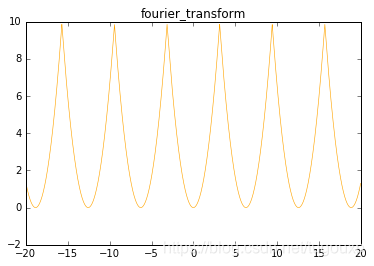
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = (pi**2)/3
s=a0
for n in range(1,300,1):
s0 = ((-1)**n)*(4/(n**2))*cos(n*(x))
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform' )
show()
fourier_wave()geogebra绘图:
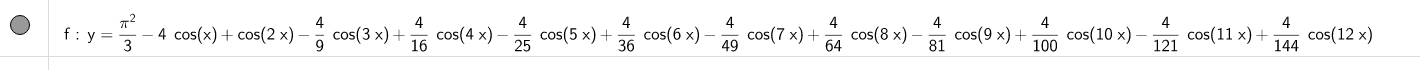

对于
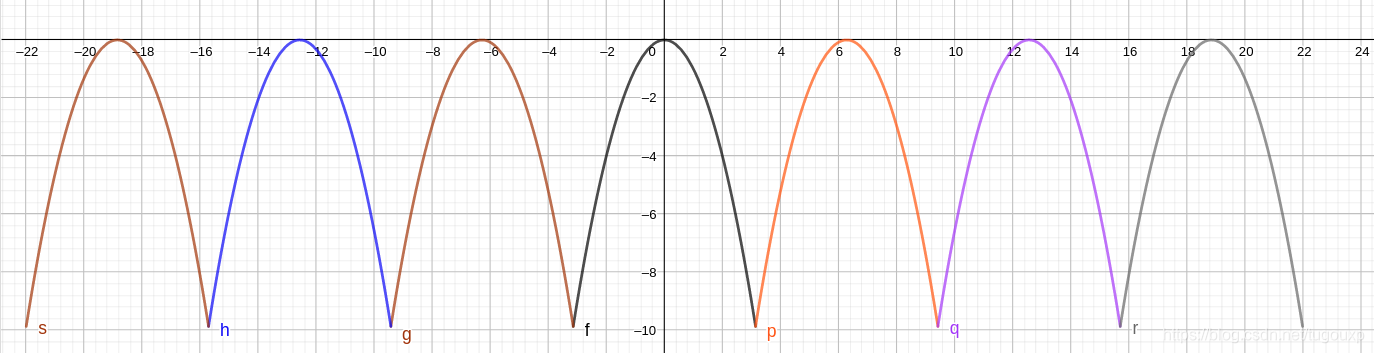
python制图:
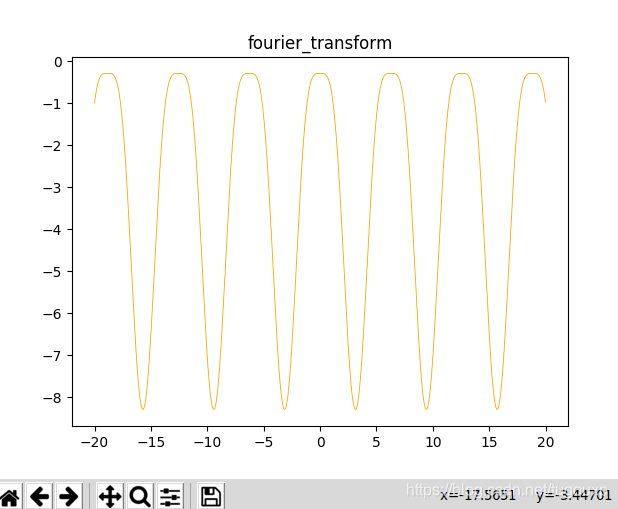
python 代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = -(pi**2)/3
s=a0
for n in range(1,300,1):
s0 = ((-1)**(n+1))*(4/(n**2))*cos(n*(x))
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform' )
show()
fourier_wave()三角波的傅里叶变换:

求解错误,实际上由于奇函数在原点对称区间求积分,
python图形:

python代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = pi/2
s=a0
for n in range(1,100,1):
s0 = ((2/((n**2)*pi)) * ((-1)**n -1))*cos(n*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()相位变化后的三角波
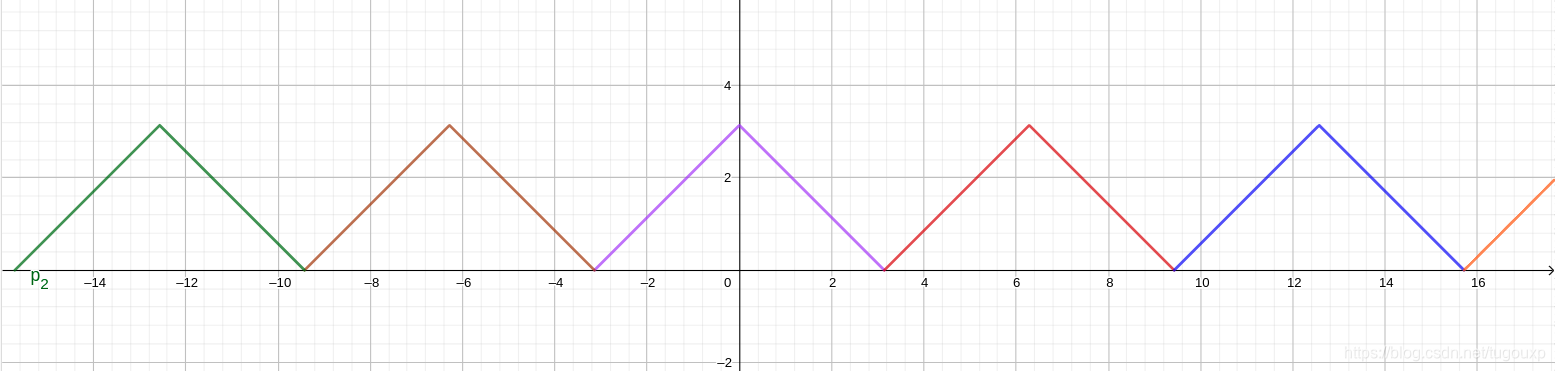
hanshu
python绘图:
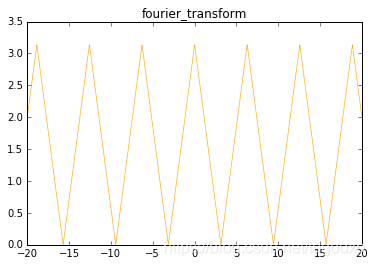
代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = pi/2
s=a0
for n in range(1,100,1):
s0 = -((2/((n**2)*pi)) * ((-1)**n -1))*cos(n*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()占空比不为1/2的方波:

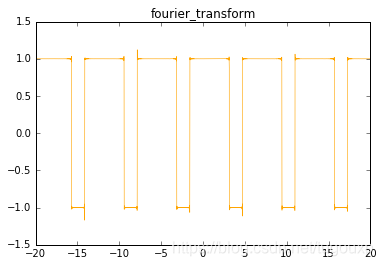
python代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = 1/2
s=a0
for n in range(1,1000,1):
if (n%4 == 0):
an = 0
bn = 0
elif (n%4 == 1):
an = 2/(n*pi)
bn = 2/(n*pi)
elif (n%4 == 2):
an = 0
bn = -4/(n*pi)
elif (n%4 == 3):
an = -2/(n*pi)
bn = 2/(n*pi)
s0 = an*cos(n*x)+bn*sin(n*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()geogebra绘图结果:
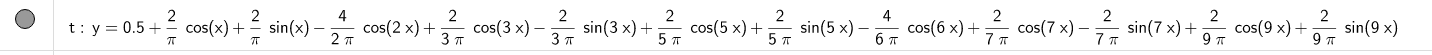

别看这个函数简单,但它妹的收敛速度太慢,9次谐波绘制才是上图的屎样,实在绘不下去了,还好python绘制的图能够说明并且保证积分过程是无误的。
函数:

python绘制的图形为:
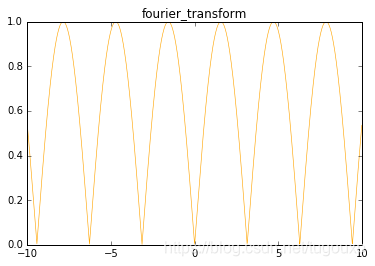
python代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-10:10:0.01]
def fourier_wave():
a0 = 2/pi
s=a0
for n in range(1,1000,1):
s0 = -4/pi * (1/(4*(n**2) -1))*cos((2*n)*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()
奇异周期函数:

积分没有问题,但发现ubuntu上用python2.7绘制的图形还不太精确,但是windows10上的anaconda则没有问题,网上说是由于广为人知的phthon2.7浮点BUG导致:
ubuntu平台绘制:

anaconda绘制:
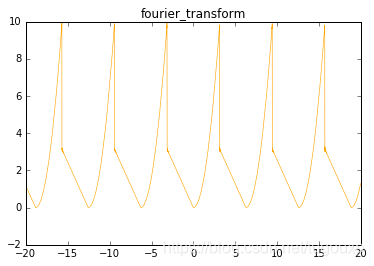
python代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = (1/2)*((pi/2)+(pi**2)/3)
s=a0
for n in range(1,1000,1):
bn = (1/(n*pi))*(pi*((-1)**n) -(pi**2)*((-1)**n) + (2*((-1)**n-1))/(n**2))
an = (((-1)**n - 1) + 2*pi*((-1)**n))/((n**2)*pi)
s0 = an*cos(n*x)+bn*sin(n*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()图象
geogebra图象:
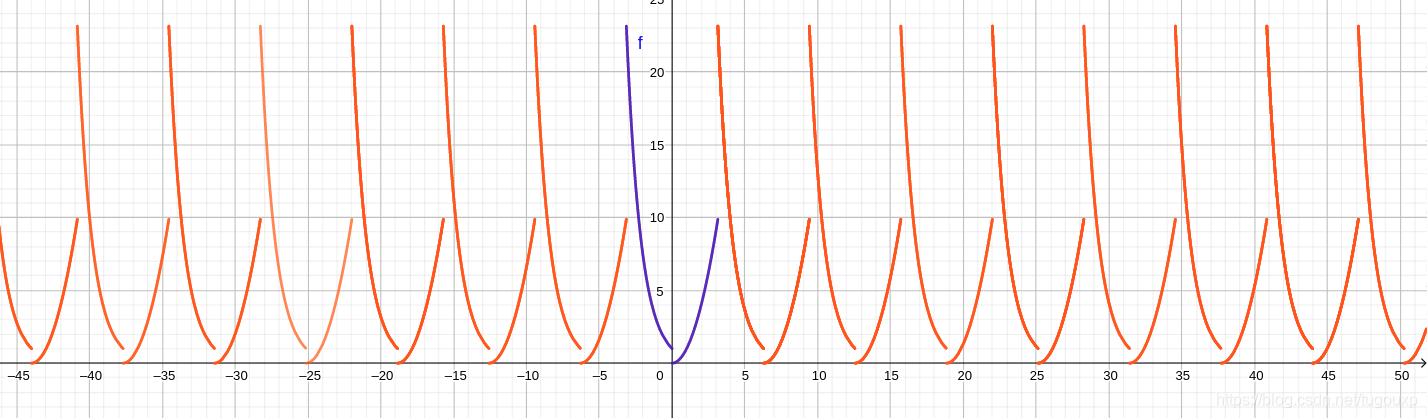
代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = (1/(2*pi))*(exp(pi)-1+(pi**3)/3)
s=a0
for n in range(1,1000,1):
bn = (1/(pi))*(((n*exp(pi)*(-1)**n)-n)/(n**2+1)+((2-n**2*pi**2)*(-1)**n - 2)/(n**3))
an = (1/(pi))*(((exp(pi)*(-1)**n)-1)/(n**2+1)+(2*n*pi*(-1)**n)/(n**3))
s0 = an*cos(n*x)+bn*sin(n*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()图像:
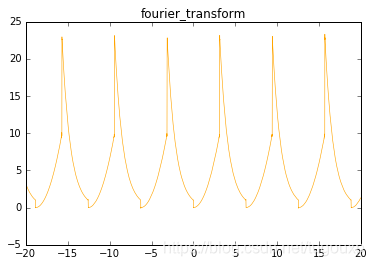
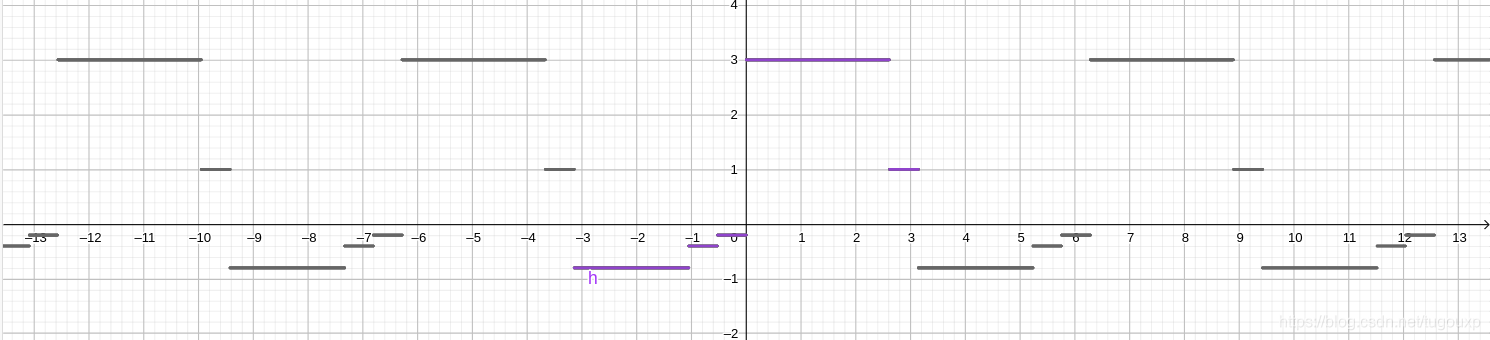
python代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-20:20:0.01]
def fourier_wave():
a0 = 61/60
s=a0
for n in range(1,1000,1):
bn = (1/(pi))*( (((-0.8)*(-cos(n*(-pi/3))) - (-0.8)*(-cos(n*(-pi))))/n) +(((-0.4)*(-cos(n*(-pi/6))) - (-0.4)*(-cos(n*(-pi/3))))/n) + (((-0.2)*(-cos(n*(0))) - (-0.2)*(-cos(n*(-pi/6))))/n)+ (((3)*(-cos(n*(5*pi)/6)) - (3)*(-cos(n*(0))))/n) + (((1)*(-cos(n*(pi))) - (1)*(-cos(n*(5*pi)/6)))/n))
an = (1/(pi))*( (((-0.8)*(sin(n*(-pi/3))) - (-0.8)*(sin(n*(-pi))))/n) +(((-0.4)*(sin(n*(-pi/6))) - (-0.4)*(sin(n*(-pi/3))))/n) + (((-0.2)*(sin(n*(0))) - (-0.2)*(sin(n*(-pi/6))))/n)+ (((3)*(sin(n*(5*pi)/6)) - (3)*(sin(n*(0))))/n) + (((1)*(sin(n*(pi))) - (1)*(sin(n*(5*pi)/6)))/n))
s0 = an*cos(n*x)+bn*sin(n*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()图像:
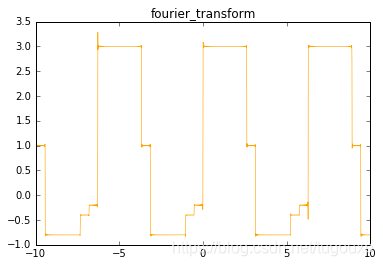
前面的周期均为的周期函数,现在用一个周期为
的函数,看有什么不同.
周期为,则基波的角速度
.
函数图形:
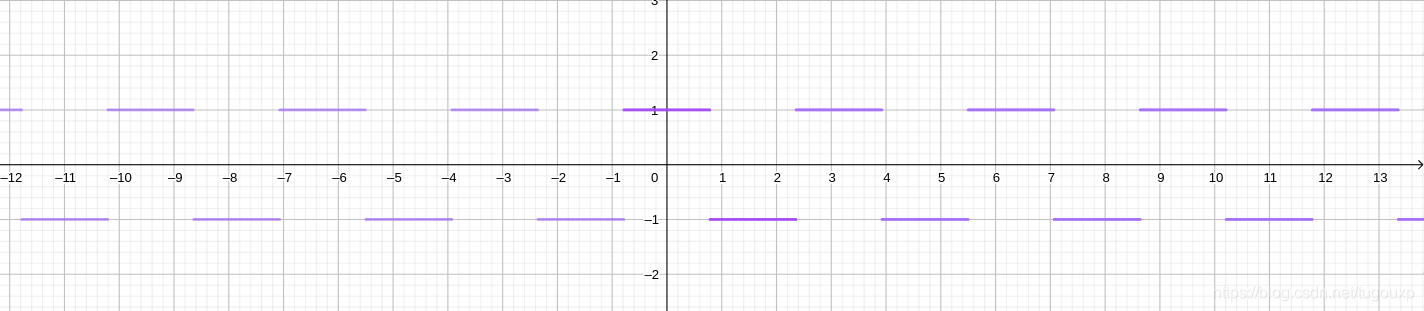
图像:
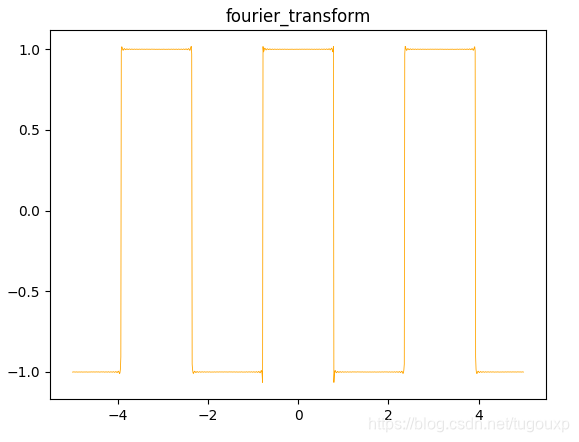
代码:
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 1 13:57:21 2021
@author: czl
"""
from pylab import *
x = mgrid[-5:5:0.01]
def fourier_wave():
a0 = 0
s=a0
for n in range(1,1000,1):
an=(1/(n*pi))*(sin(2*n*pi/4) - sin(-2*n*pi/4)) - (1/(n*pi))*(sin(2*n*3*pi/4) - sin(2*n*pi/4))
bn=0
s0 = an*cos(2*n*x)+bn*sin(2*n*x)
s=s+s0
plot(x,s,'orange',linewidth=0.6)
title('fourier_transform')
show()
fourier_wave()参数信息:
geogebra图像是:
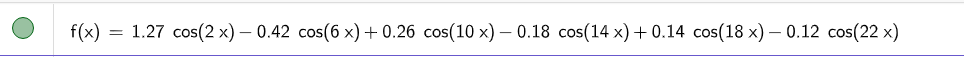

也是,完美符合!
实践证明,迪利克雷条件真是比较宽松的条件,宽松到,几乎可以做出论断,但凡周期函数,皆可傅里叶!
最后,以几张图结尾,下图是方波在各次1-17谐波时候的图形,最高次是红色代表17次谐波图形,,也是最接近方波的。
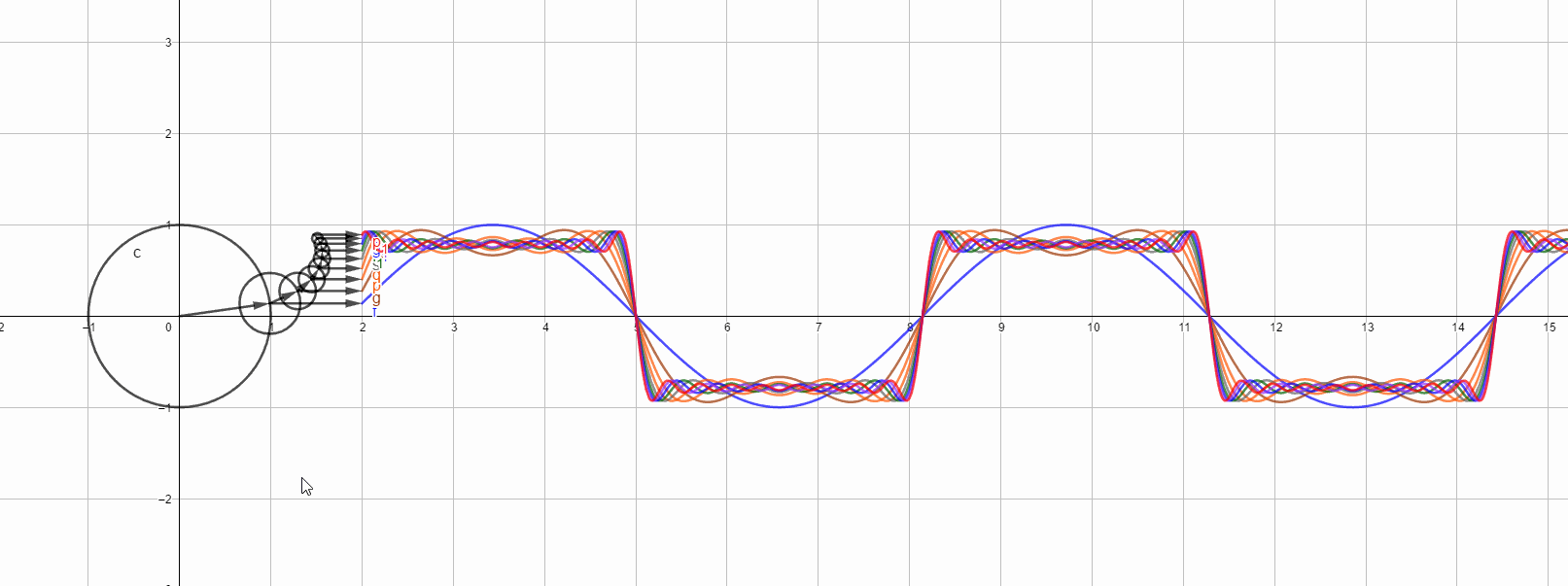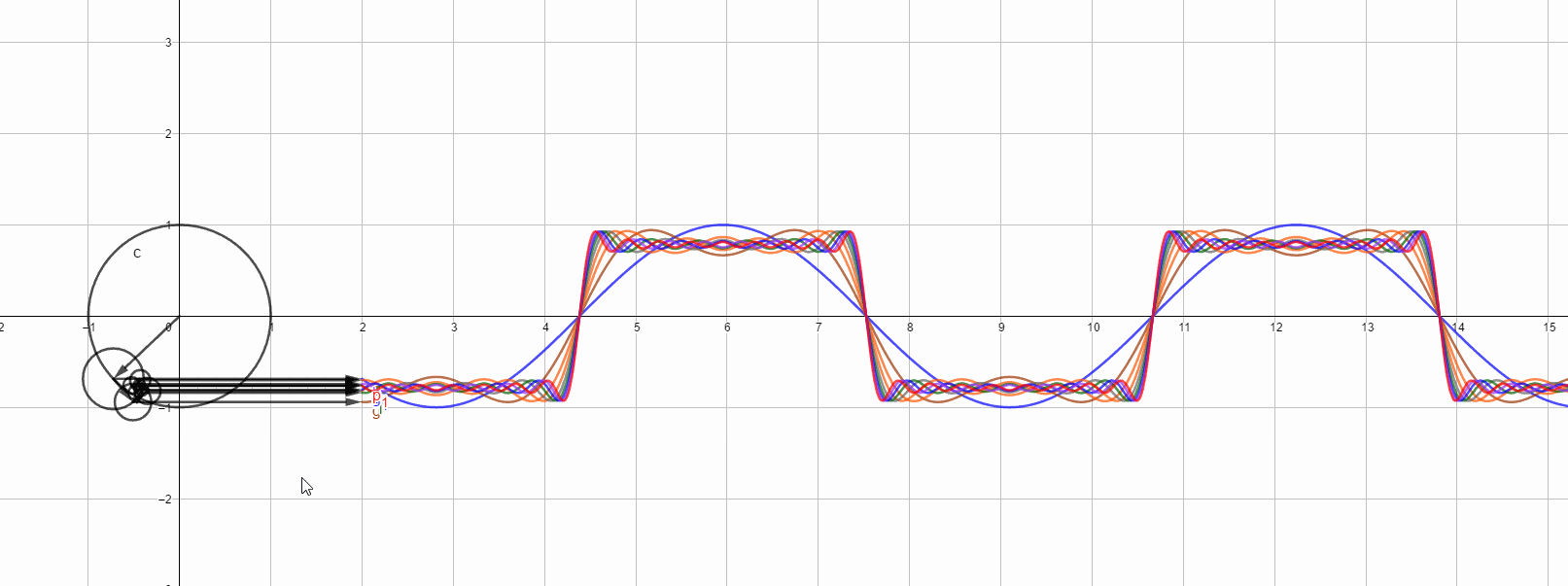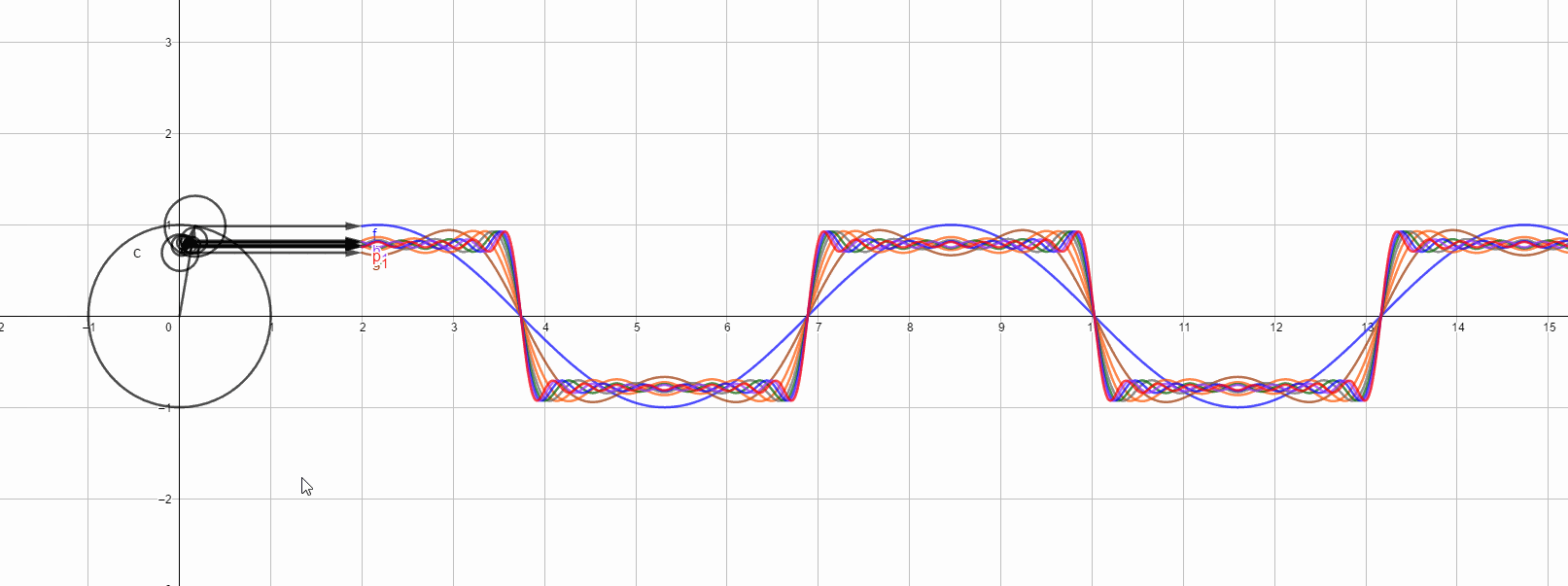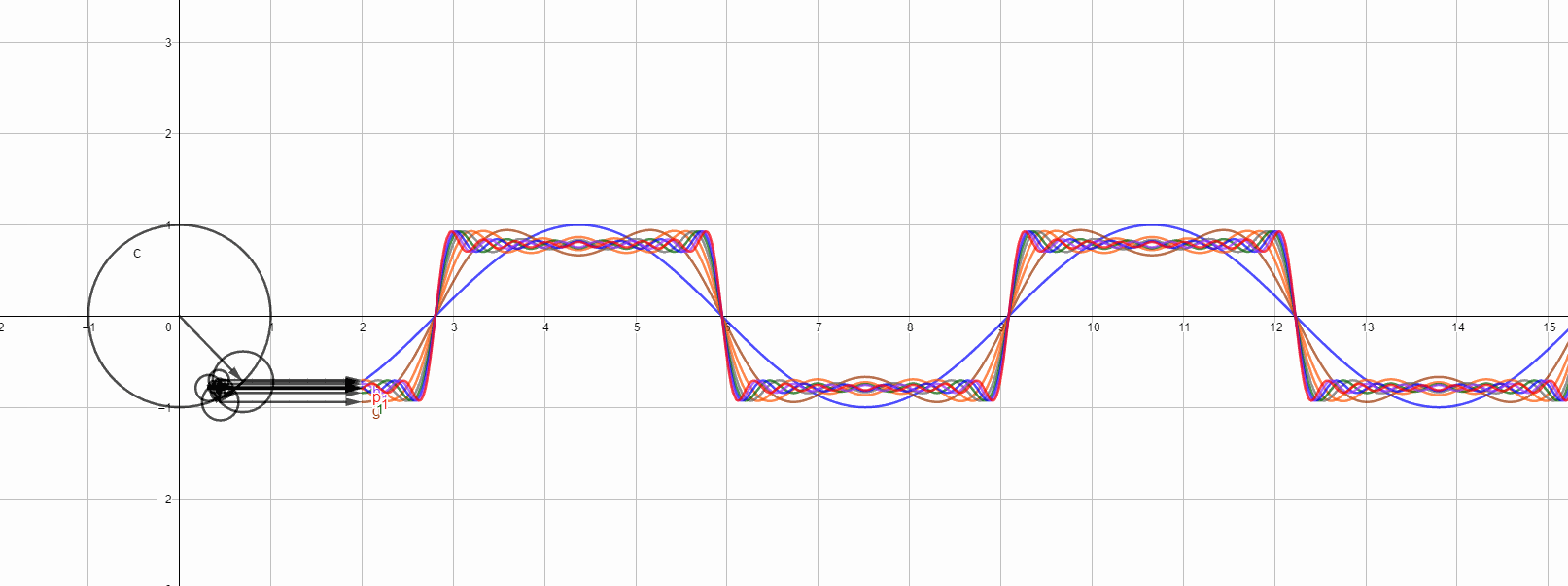
单独看17次谐波的结果:

锯齿波的傅里叶变换直观图,最高次8次谐波。
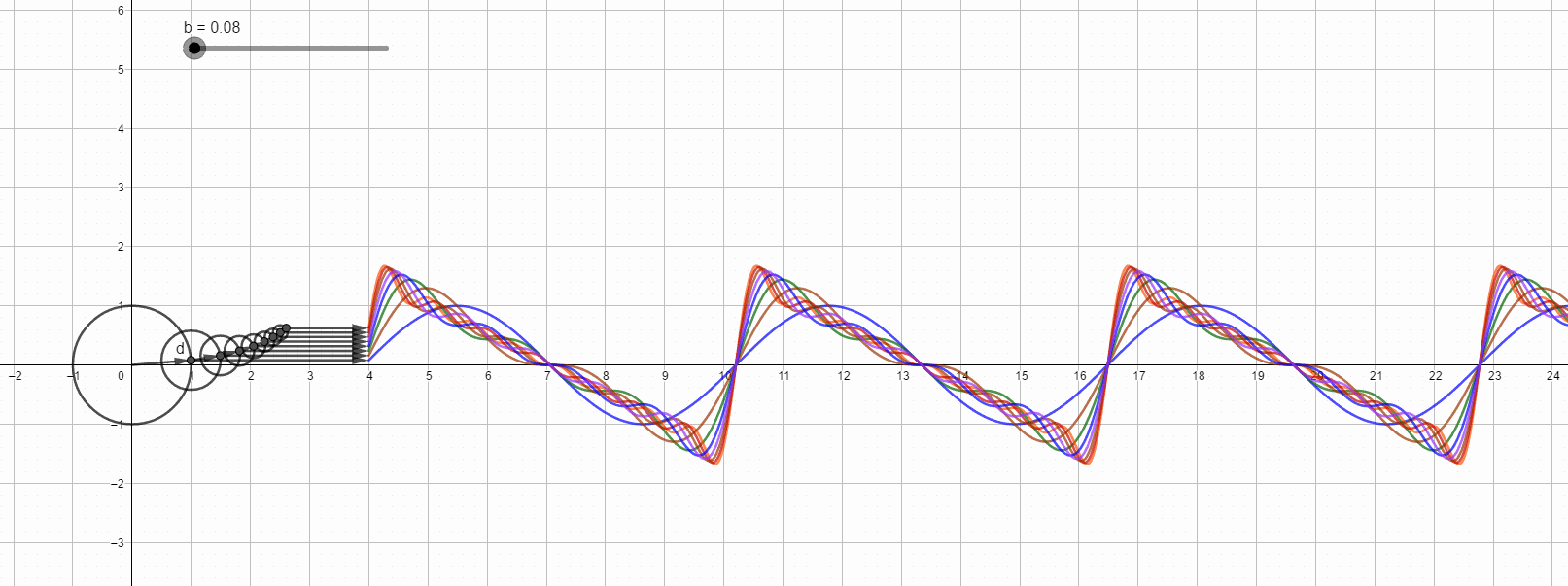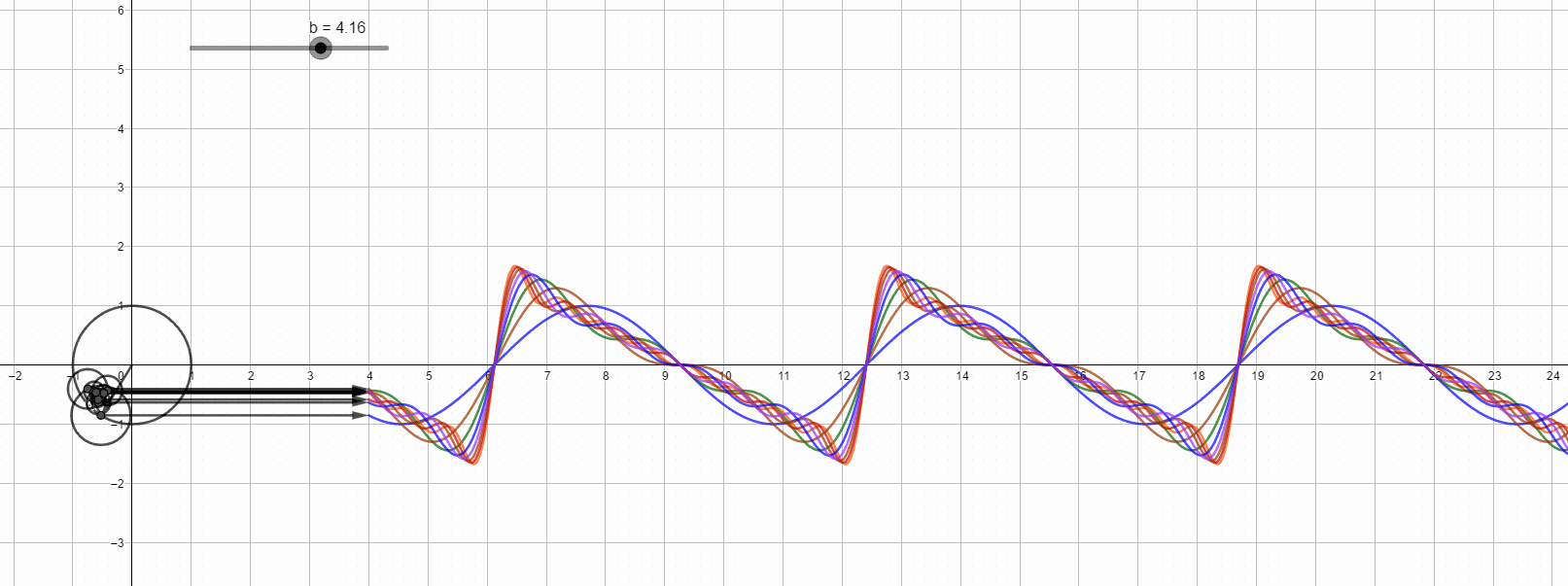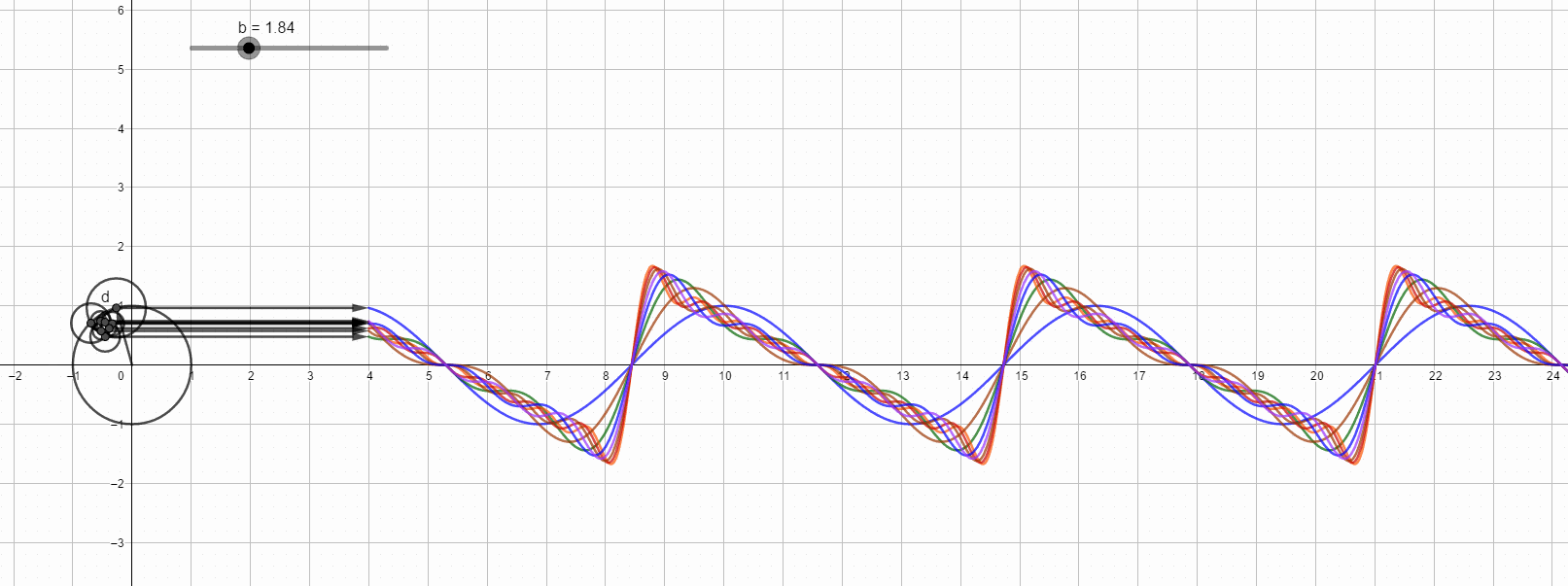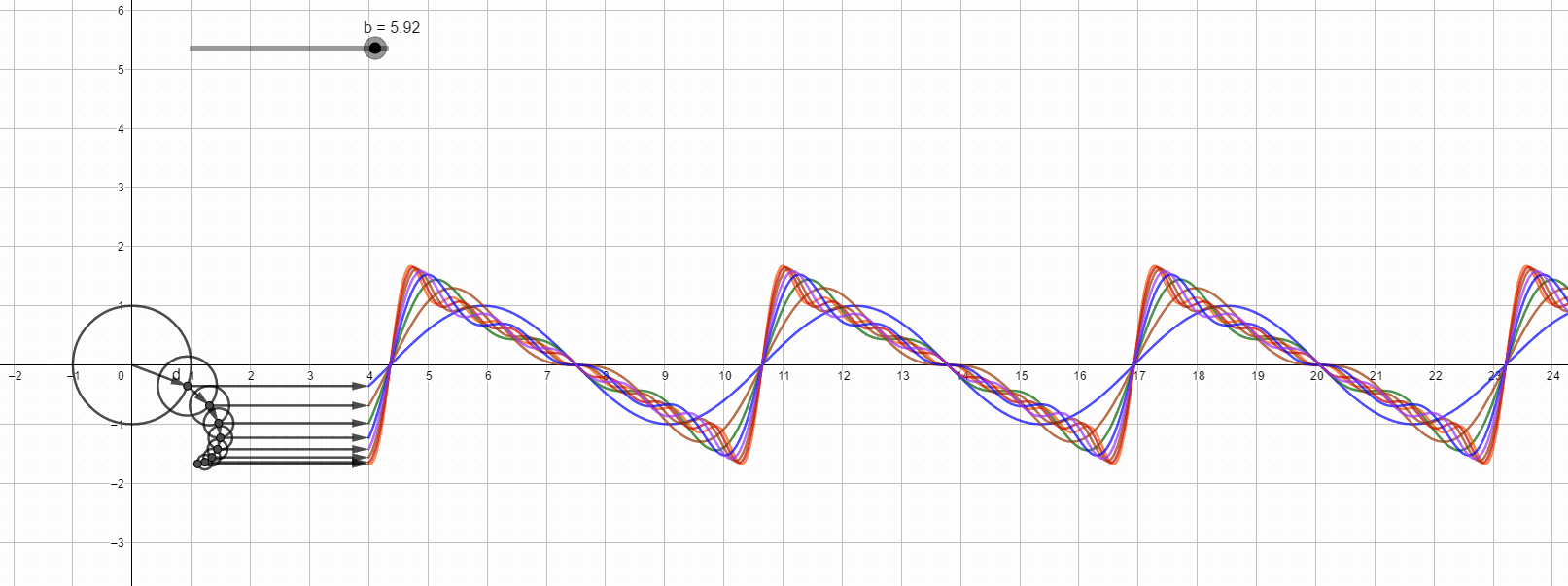
第八次谐波的情况:
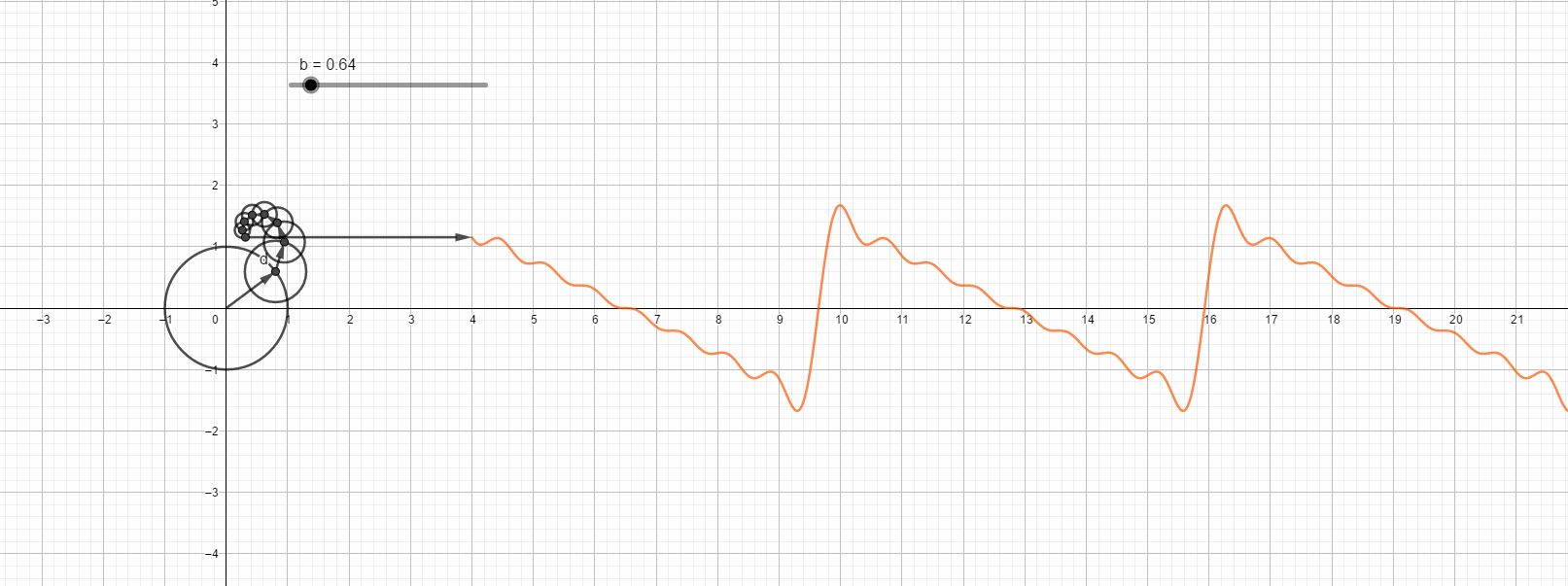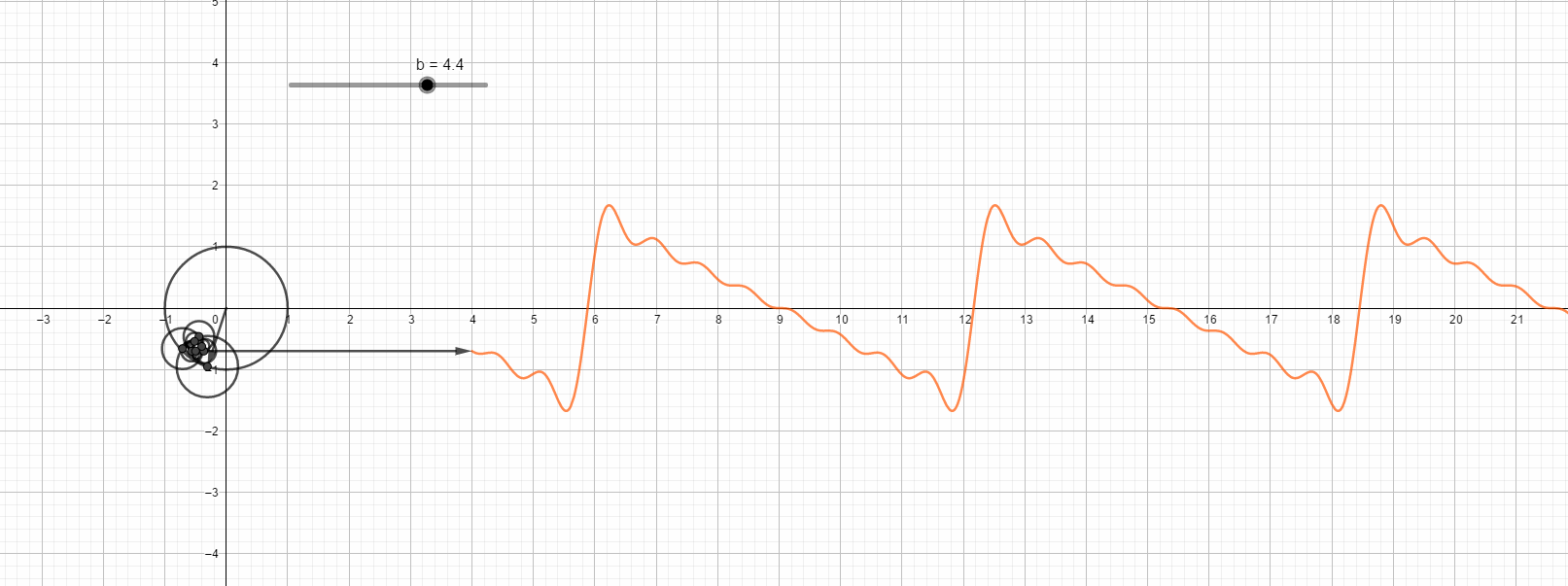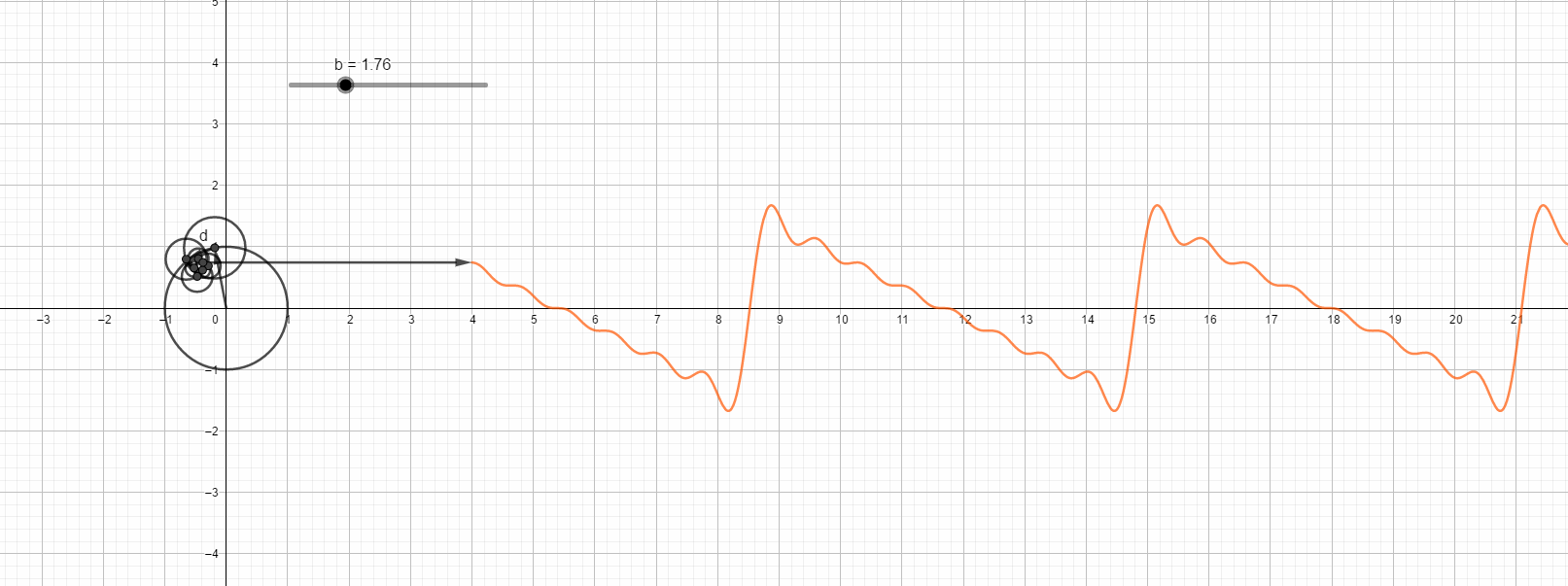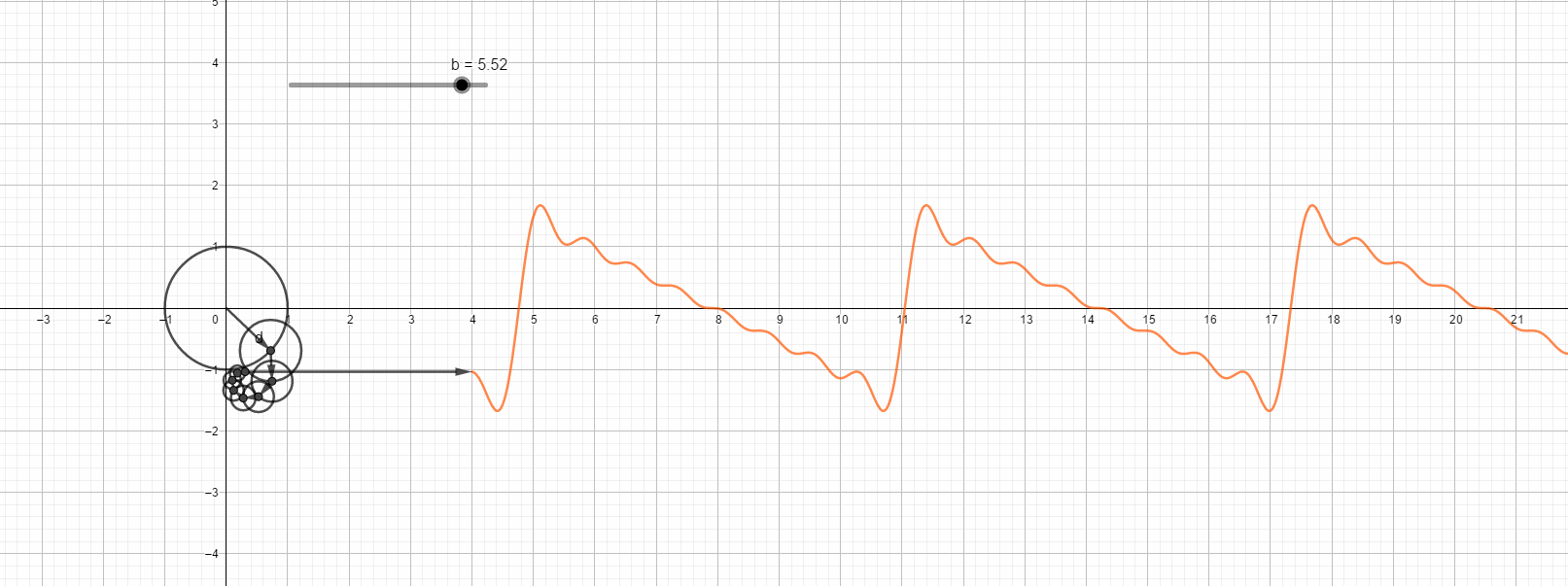
下面这幅图很有意思,它说明同样角度的正弦和余弦级数多项式和图形并不一定相似:
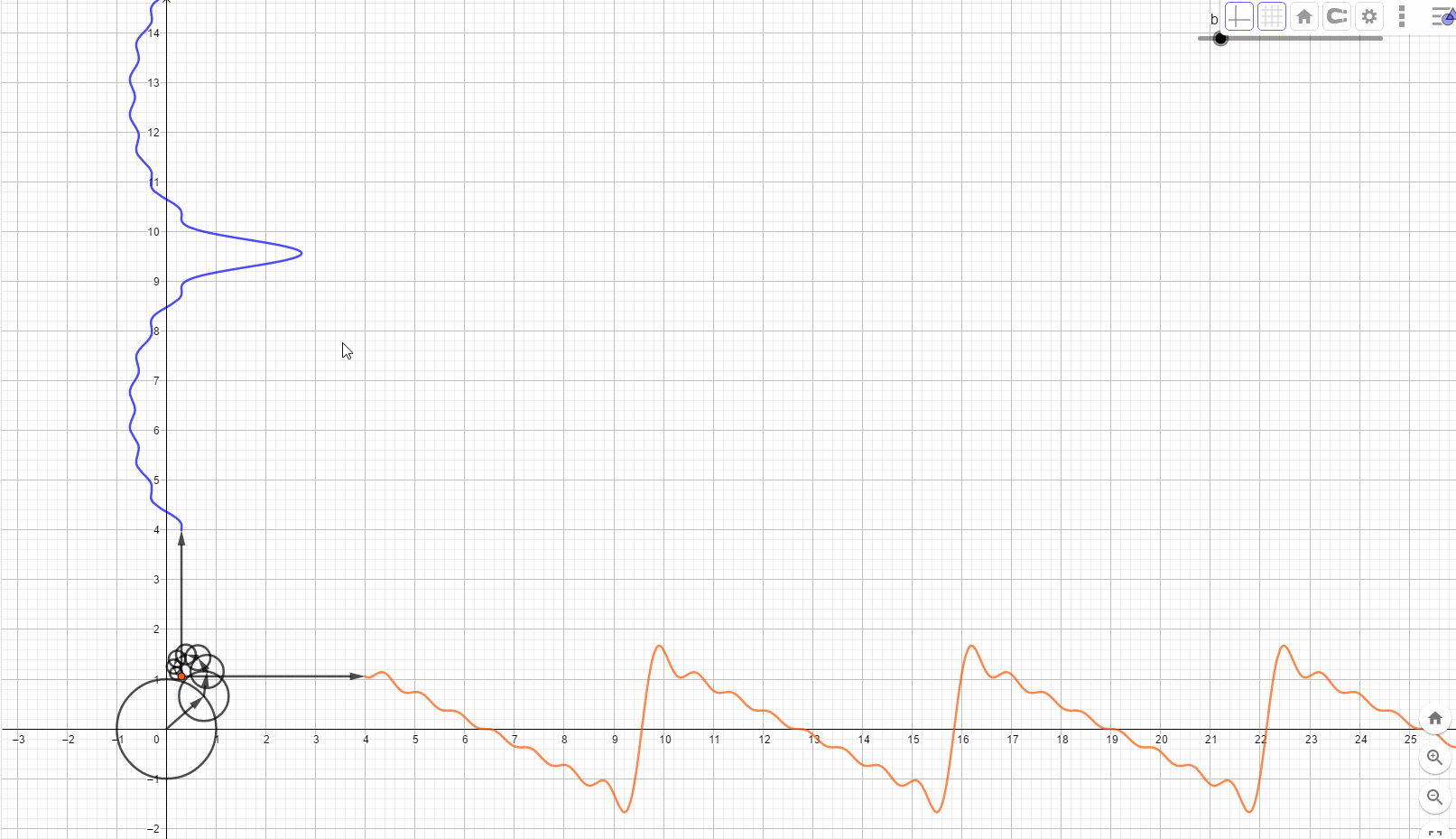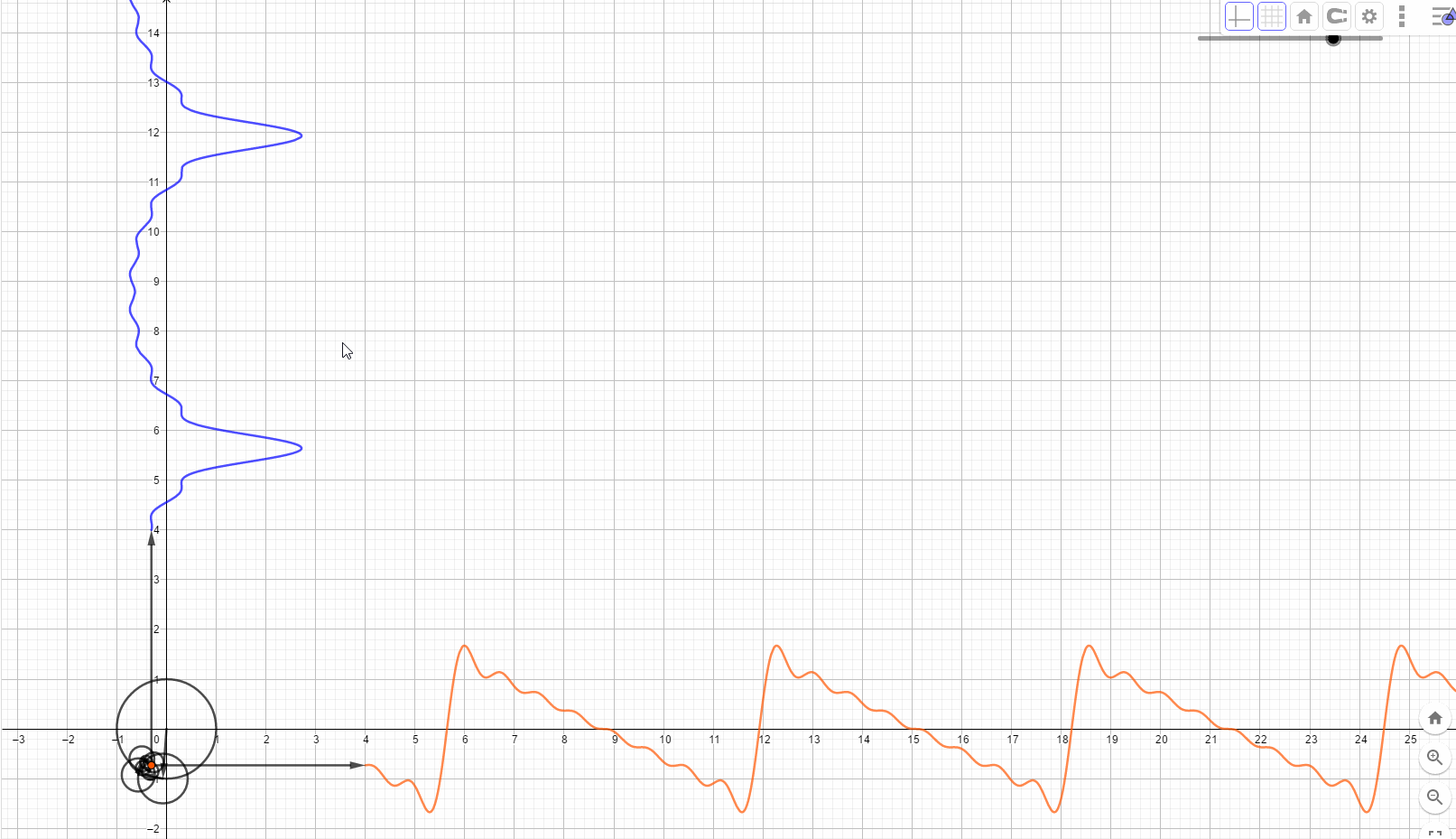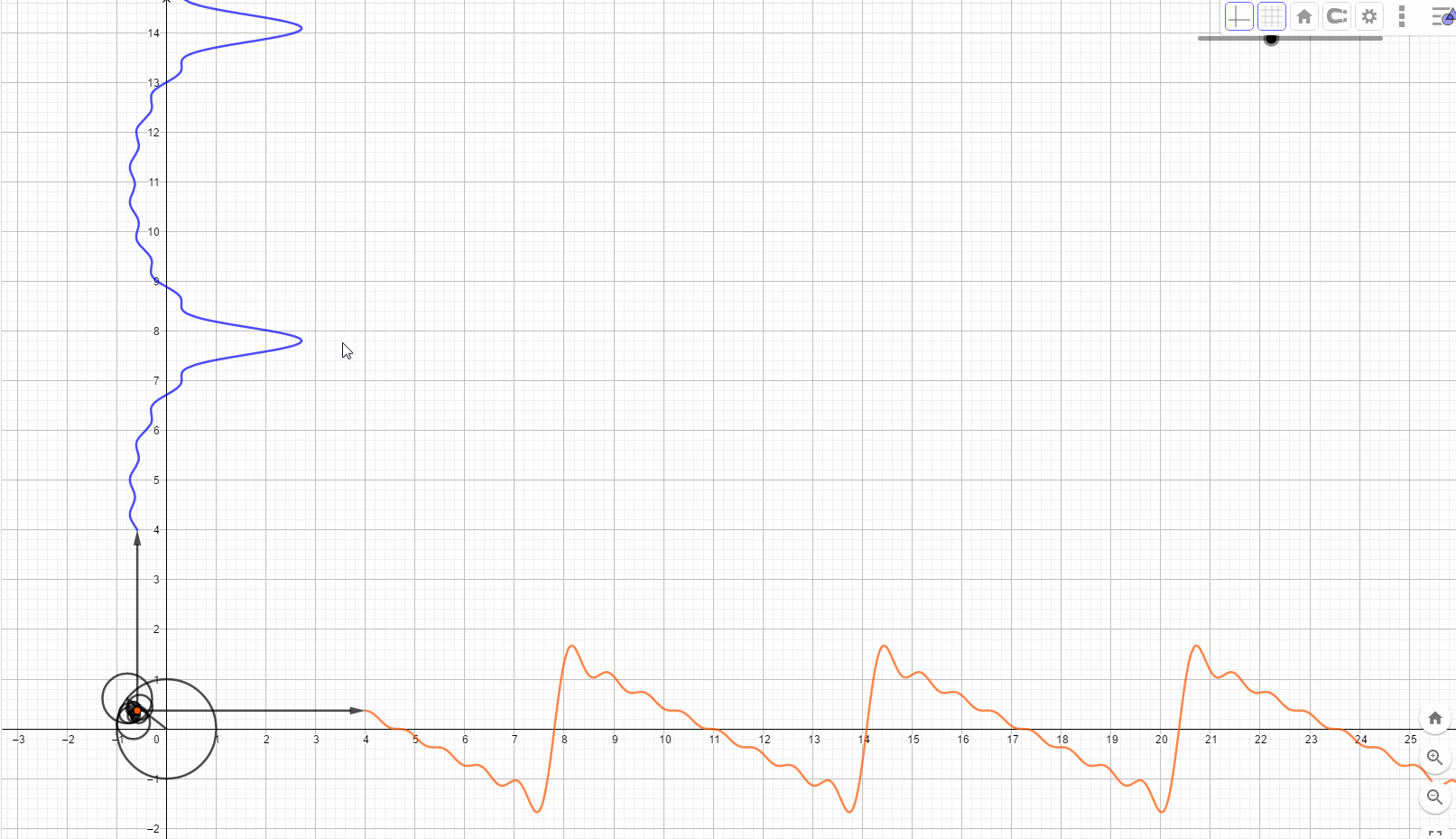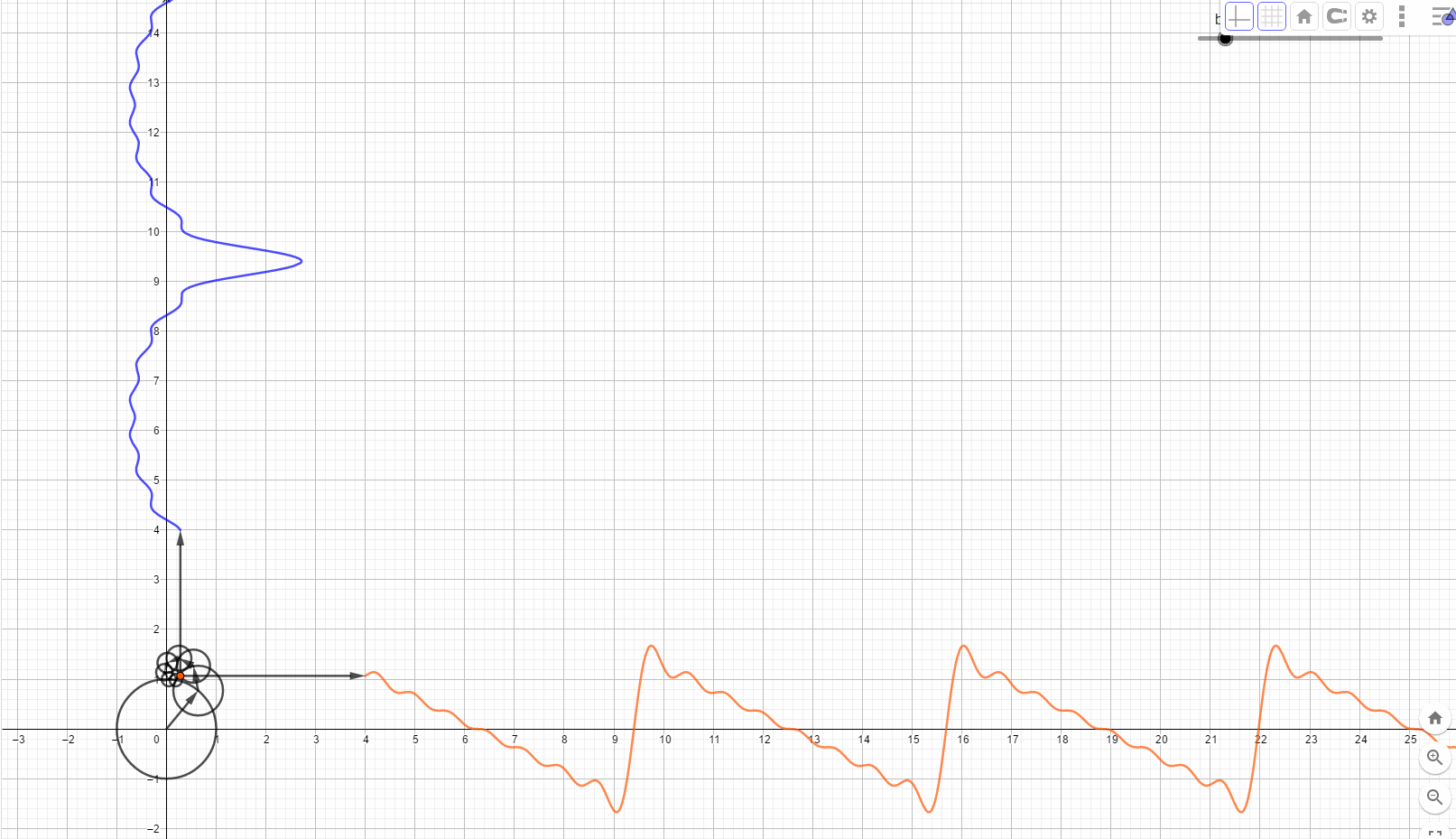
在频域看世界,世界是静止的,因为只有一组不变的频率摆在那里。 我们的世界有着统一而优美的运行机制,这使我想到,在现实生活中看到的纷繁复杂的现象,有没有可能是同一个事物的不同角度在这个世界的投影。想象一下,世界上每一个看似混乱的表象,背后实际上都是一条时间轴上按照或有或无的规则变化的曲线,这些曲线都是由无穷无尽的正弦波叠加而成。这些看似不规则的变化,内蕴的竟然是规则的正弦波在时间上的投影,那么你的脑海中会产生一个什么画面呢?
我们眼中的世界就像是皮影戏的大屏幕,幕后面有无数的齿轮,大齿轮带动小齿轮,小齿轮带动更小的,在最外面的齿轮上有一个小人投影到屏幕上,那就是我们看到的,我们知道这个小人在按照有或者无的规律表演,却看不透它背后的驱动机制。
这个小人会思考吗?它会是我们吗? 真的有自由意志吗?还是一切都是确定好的?