朴素贝叶斯分类的定义如下:
1. 设 x = a1,a2, ...,am为一个待分类项,而每个a是x的一个特征属性。
2.待分类项的类别集合C={y1,y2,...,yn}
3. 计算 p(y1|x)...p(yn|x)
4.如果p(yk|x) = max{ p(y1|x)...p(yn|x)}, 则x 类别为yk。
那么现在的关键就是如何计算第三步中的各个条件概率:
1.找到一个已知分类的待分类项集合(训练集)。
2. 统计得到的各个类别下各个特征属性的条件:
P(a1|y1),...,P(a1|yn),。。。,P(am|y1),...,P(am|yn) 可以看出生成的是一个m * n存储的矩阵
3. 朴素贝叶斯假设各个特征属性之间相互独立,根据贝叶斯定理推导:
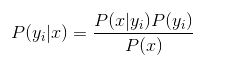
分母对于所有类别而言是常数,因此可以忽略。又因为各个feature之间相互独立,所以:
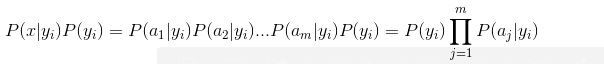
Summary:naive beyes 是生成模型,根据先验概率 P(X)和条件概率 P(X|Y)求出联合分布概率P(XY),在根据beyes定理可以求出
后验概率P(Y|X)。
hint:在某个类别概率为0的情况下怎么办?
在一些情况下,由于样本数据极度匮乏,很有可能出现某个特征的取值和某个类别的取值在训练集中从未同时出现过,即 #{X_i=x_iΛC=c_k} = 0,这会造成对 P(X_i=x_i|C=c_k) 的估计等于零。P(X_i=x_i|C=c_k) = 0 会导致对应的 P(C=c_k) × Π_i P(X_i=x_i|C=c_k) = 0,即让我们误以为这个样本属于某个类别 c_k 的概率为 0。这是不合理的,不能因为一个事件没有观察到就认为该事件不会发生。
解决这个问题的办法是给每个特征和类别的组合加上给定个数的虚假样本(“hallucinated” examples)。假设特征 X_i 的取值有 J 个,并假设为每个 x_i 对应的 #{X_i=x_iΛC=c_k} 增加 s 个虚假样本,这样得到对 P(X_i=x_i|C=c_k) 的估计称为平滑估计(smoothed estimate):
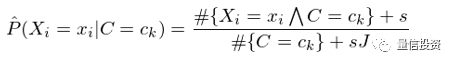
特别的,当 s = 1 时,上述平滑称为拉普拉斯平滑(Laplace smoothing)。类似的,对于 P(C=c_k) 的估计也可以采用平滑的方式:
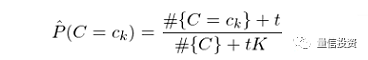
其中,t 为对每个类增加的虚假样本数,K 是类别个数,#{C} 表示训练集的样本数。
当特征是连续变量时,情况稍微复杂一些。在使用训练集求解 P(X_i=x_i|C=c_k) 时,需要假设该条件概率分布的形式。一种常见的假设是认为对于给定的 c_k,P(X_i=x_i|C=c_k) 满足正态分布,而正态分布的均值和标准差需要从训练集学习得到。这样的模型称为高斯朴素贝叶斯分类器
被广泛应用于文本分类和垃圾邮件过滤等领域。