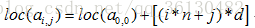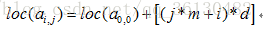从逻辑结构上讲,数组结构可以看做对一般的线性表的补充。一维数组即为线性表,二维数组可以看作是元素为一维数组的(线性表的)线性表,以此类推n维数组为元素为n-1维数组的线性表。
行主映射和列主映射
数组的应用需要我们将数组元素序列化,即按一维数组排列 。令n是一个k维数组的元素个数。
- 行为主序的优先存储是将数组元素按行优先关系进行排列,,第i+1行元素紧跟在第i行元素的后面,同一行元素按照列下标次序排列
- 列为主序的优先存储是将数组元素按列优先关系进行排列,,第j+1列元素紧跟在第j列元素的后面,同一列元素按照行下标次序排列
数组元素地址的计算
- 二维数组A有m行,n列,按照行优先存储在内存中,假设每一个数组元素占d个存储单元,下标从0开始。则有
同理以列为主序的顺序存储其地址计算公式为
- 三维数组的地址计算
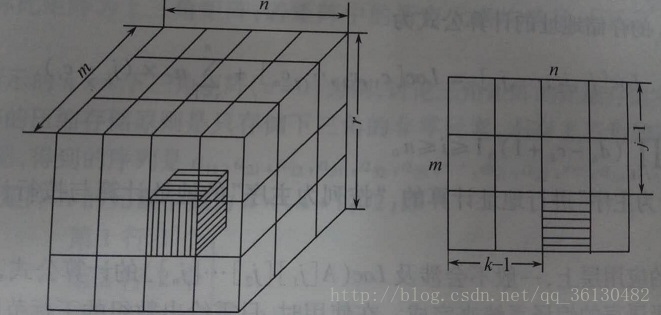
三维数组[1..r,1..m,1..n]可以看做是r个m*n的二维数组,如图所示。
假定每个元素占size个存储单元,采用以行为主许的方法存储。首元素从1开始。显然
loc(A[i][1][1])=loc(A[1][1][1])+(i-1)*m*n 因为在该元素之前,有i-1个m*n的二维数组。故由二维数组地址计算方法推得
loc(A[i][j][k])=loc(A[1][1][1])+[(i-1)*m*n+(j-1)*n+k-1]*size 推导到一般情况,用下标依然使用i,j,k并且下限分别为c1,c2,c3,上限分别是d1,d2,d3,每个元素占size个存储单元
loc(A[i][j][k])=loc(A[1][1][1])+[(i-c1)**(d2-c2+1)*(d3-c3+1)+(j-c2)*(d3-c3+1)+k-c3]*size 矩阵
一个m*n的矩阵是一个m行,n列的表,m和n是矩阵的维数。
三角矩阵
元素分布具有一定规律的矩阵成为规律分布的矩阵,如三角矩阵,带状矩阵,抑制二维矩阵A中的元素下标i,j,作为转换函数F的自变量,计算出相应一维内存空间地址值K,即A[i][j]=B[K],实现原二维数组到压缩存储之后的一维数组的存储映射。
| 三角矩阵 | 性质 |
|---|---|
| 上三角矩阵 | i > j时,有a[i][j] = 0 |
| 下三角矩阵 | j> i时,有a[i][j] = 0 |
| 对角阵 | i!=j时 a[i][j] = 0, |
由于下三角矩阵A的元素个数为n*(n+1)/2即可将A存储到大小为n*(n+1)/2的一维数组B中。下三角矩阵中元素a[i][j] (i>j)在一维数组B中的存储地址为(下标从1开始,按行为主序):
loc[i,j]=loc[1,1]+(前i-1行非零元素+第i行a[i][j]之前非零元素个数)*size
其中,前i-1行元素个数为i*(i-1)/2,第i行a[i][j]之前非零元素个数=j-1;
即loc[i,j]=[i*(i-1)/2+j-1]*size带状矩阵
带状矩阵的所有非零元素都集中在对角线为中心的带状区域。其中最常见的为三对角矩阵。

带状矩阵特点,在以下条件下a[i,j]非零,其他元素均为0.
- 当i=1时,j=1,2
- 当 1< i< n时,j=i-1,i,i+1
当 i=n时,j=n-1,n
故根据上述特点引出带状矩阵亚索存储方法,其原则为:将带状区域上的非零元素按照行序存储,压缩方法如下。确定存储该矩阵所需要的一维向量空间的大小。假设每个非零元素占空间大小为size,那么一维向量空间大小为
2+2+(n-2)*3=3*n-2- 确定元素在一维空间中的位置
loc(A[i][j])=loc(A[1][1])+(前i-1行非零元素个数+第i行a[i,j]之前非零元素个数)*size
=loc(A[1][1])+(3*(i-1)-1+j-i+1)
=loc(A[1][1])+(2*(i-1)+j-1)