最优二叉查找树，动态规划法，二维表，填表优化，代码

    笔者先介绍一下动态规划法最优二叉查找树以及填表公式（本质是想吐槽其繁琐）。

    设T(i, j)是由记录{ri, …, rj}(1≤i≤j≤n)构成的二叉查找树，C(i, j)是这棵二叉查找树的平均比较次数。虽然最后的结果是C(1, n)，但遵循动态规划法的求解方法,需要求出所有较小子问题C(i, j)的值，考虑从{ri, …, rj}中选择一个记录rk作为二叉查找树的根结点，可以得到如下关系：

    设一个二维表C[n+1][n+1]，其中C[i][j]表示二叉查找树T(i, j)的平均比较次数。二维表R[n+1][n+1]，其下标范围与二维表C相同，R[i][j]表示二叉查找树T(i, j)的根结点的序号。

    想要得到两个二维表的值，需要按照公式去计算每个C[i][j]，这对于笔者这样讨厌繁琐的人来说是致命的，所以笔者尝试去寻找表中的规律，幻想不用公式，却能快速求出准确的值。事实证明规律是存在的。

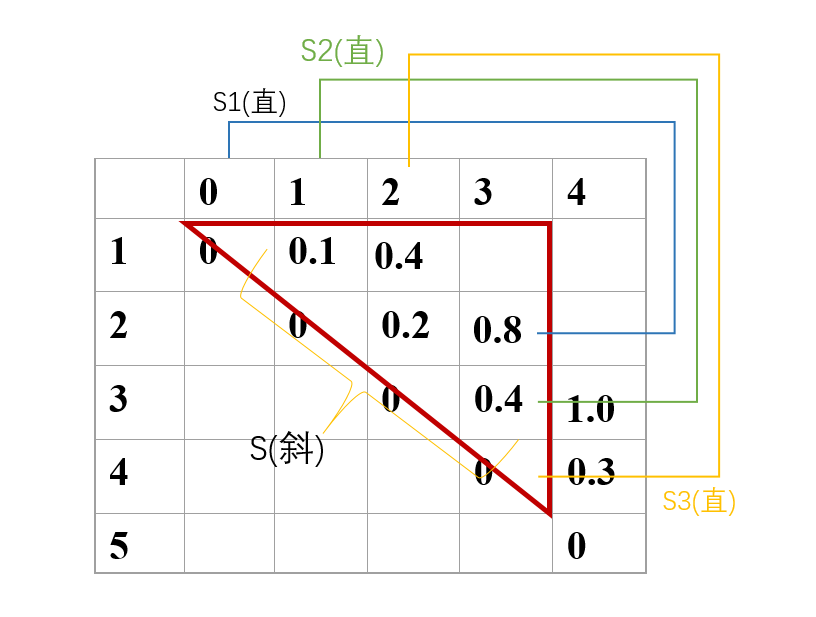
    求C[i][j]时，设以C[i][i-1],C[j+1][j],C[i][j]三个点形成的直角三角形的次斜边上的值累加和为S(斜)，直角边上对应两点的和为S(直)，显然S[直]有j-i+1个，则C[i][j]=S[斜]+min{S[直]}。下面举个例子求C[1][3]的值，如图所示：

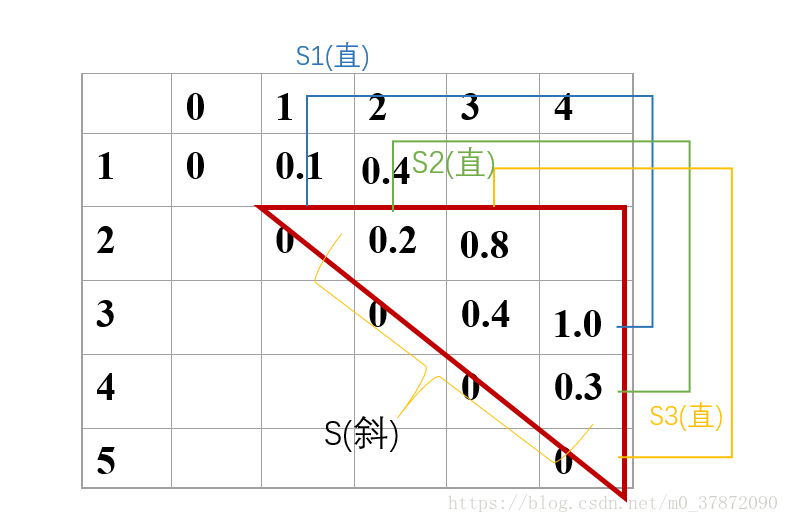
    S(斜)=0.1+0.2+0.4=0.7，S(直)=min{S1(直),S2(直),S3(直)}=min{0+0.8,0.1+0.4,0.4+0}=0.4，则C[1][3]=0.7+0.4=1.1。同理，求C[2][4]，如下图所示，C[2][4]=1.4：

    其实本质没有发生改变，只是把数学公式图形化，方便填表。最优二叉查找树代码如下：

void OptimalBST(double a[],double b[],int n,double **R,int **mink,double **C)
{
	//初始化
	for(int i=0; i<=n; i++)
	{
		C[i+1][i] = a[i];
		R[i+1][i] = 0;
	}
	for(int d=0; d<n; d++) 
		for(int i=1; i<=n-d; i++) //对角线逐条计算
		{ 
			C[i][j]=C[i][j-1]+a[j]+b[j];
			R[i][j]=R[i+1][j];
			mink[i][j]=i;
			for(int k=i+1; k<=j; k++)
				if(R[i][k-1]+R[k+1][j]<R[i][j])
				{
					R[i][j]= R[i][k-1]+R[k+1][j];
					mink[i][j]=k; 
				}
			R[i][j]+=C[i][j];
		}
}