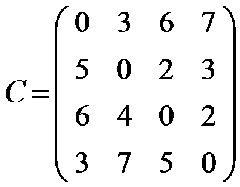算法探秘（一）动态规划法解决TSP,多段图路径,0/1背包问题,最长公共子序列,二叉查找树问题

引言

背景

• 为什么要动态规划：为研究最优化问题提出的概念，是一种求解多阶段决策最优化问题的工具。
• 优势：将每个子问题只求解一次并保存在表中，下次查表获得解，免去重复计算。

相关概念

1.最优化问题

满足约束条件的解称为问题的可行解，这些标准通常以函数的形式给出，这些标准函数称为目标函数，使目标函数取得极值（极大或极小）的可
行解称为最优解，这类问题就称为最优化问题。

2.多阶段决策

前一阶段决策所采取的动作，成为下一阶段决策的依据。决策序列在不断变化的状态中产生。这个决策序列产生的过程称为多阶段决策过程。

3.最优性原理

各子问题的解只与其前面的子问题的解相关，且各子问题的解都是相对于当前状态的最优解，整个问题的最优解由各个子问题的最优解构成。

4.动态规划法的设计思想

将子问题的解求解一次并填入表中。当需要再次求解此子问题时，可以通过查表获得该子问题的解而不用再次求解，从而避免了大量重复计算。

• 用动态规划法求解的问题具有特征：
  ✓ 能够分解为相互重叠的若干子问题。
  ✓ 满足最优性原理：该问题的最优解中也包含着其划分出子问题的最优解。

• (用反证法)分析问题是否满足最优性原理：
  ✓ 先假设由问题的最优解导出的子问题的解不是最优的。
  ✓ 然后再证明在这个假设下可构造出比原问题最优解更好的解，从而导致矛盾。

接下来我们分析图问题，组合问题和查找问题三类问题中动态规划法的应用。

图问题中的动态规划

TSP问题

1.问题定义

TSP问题是指旅行家要旅行n个城市，要求各个城市经历且仅经历一次然后回到出发城市，并要求所走的路程最短。(在有向带权图G=<V,E>中，寻找路径最短的哈密尔顿问题。)
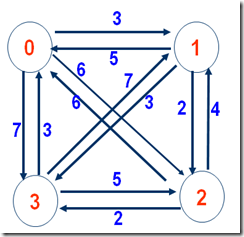
假设现在有四个城市，0,1,2,3，他们之间的代价如图一，可以存成二维表的形式

2.引入方程

• $d(i, V’)$:从顶点i出发经过V’(是一个点的集合) 中各个顶点一次( $V’$中的点是已经经过的点集)，最后回到出发点s的最短路径长度。当V’为空集，那么 $d(i, V’)$，表示从i不经过任何点就回到s。
• $C_{ik}$表示你选择的城市 $k$和城市 $i$的距离， $d(k, V’-{k})$是一个子问题
• TSP的动态规划函数（递推式）为：
  $d(i,V-{i})=d(i,V’)= min \{c_{ik}+d (k,V’－{k})\} (k∈V’)$
  

3.建立表格

$eg.\,\,\,\,d(1, \{2\})= c_{12}+d(2,\{\})=2+6=8(1→2)$说明:j是要回s要经过但还没经过的点集，为空代表不经过任何点就回到s。

扫描二维码关注公众号，回复： 10971857 查看本文章

小感悟

大块的最优依赖小块的最优，先解小块，再出大块，最后选定最优解。

多段图的最短路径

1.问题定义

设 $G=(V,E)$是一个赋权有向图，其顶点集 $V$被划分为 $k(k>2)$个不相交的子集 $V_{i(1\leq i \leq k)}$，其中， $V_1$和 $V_k$分别只有一个顶点 $s$(称为源)和一个顶点 $t$(称为汇)，所有的边 $(u,v)$的始点和终点都在相邻的两个子集 $V_i$和 $V_{i+1}$中： $u\in V_i,v\in V_{i+1}$, 且边 $(u,v)$有一个正权重，记为 $\omega_{(u,v)}$.请设计一个算法，求解从源s到汇t的权重之和最小的路径。

2.引入方程

• $(u, v)$：多段图的边
• $c_{uv}$:边上的权值
• $d(s, t)$:从源点 $s$到终点t的最短路径记为，则从源点0到终点9的最
  短路径 $d(0, 9)$由下式确定：
  $d(0, 9)=min{c01+d(1, 9), c02+d(2, 9), c03+d(3, 9)}$

$............$

分析思路同TSP问题。

组合问题中的动态规划法

0/1背包问题

1.问题定义

给定 $n$种物品和一个背包，物品 $i(1≤i≤n)$的重量是 $\omega_i$，其价值是 $v_i$ ，背包的容量为 $C$，对于每种物品只有两种选择，即装入背包或不装入背包。问题是如何选择装入背包的物品使得装入背包的物品的总价值最大？

2.引入方程

最优解方程

$\left \{ \begin{aligned} &\sum_{i=1}^n{\omega_ix_i}\leq C\\ &x_i∈\{0,1\} &(1 \leq i \leq n) \end{aligned} \right.$

$max{\sum_{i=1}^nv_ix_i}$

价值方程

1.背包不足以装入物品 $i$，则装入前 $i-1$个物品所得到的最大价值相等，即 $x_i=0$，背包不增加任何价值。
2.背包容量可以装入物品 $i$，此时可能存在两种情况，即考虑装与不装？

• 若把第 $i$个物品没有被装入背包，则与第一种情况相同

• 若把第 $i$个物品装入背包，则背包中物品的总价值等于把前 $i−1$个物品装入容量为 $j−ω_i$的背包中得到的最大价值加上第 $i$个物品装入背包的价值 $v_i$，公式如下：

  $V(i,j)= \left \{ \begin{aligned} &V(i-1,j)&j<w_i\\ &max \{V(i-1,j),V(i-1,j-\omega_i)+v_i\}&j\geq \omega_i \end{aligned} \right.$

范例

例如，有5个物品，其重量分别是 ${2, 2, 6, 5, 4}$，价值分别为 ${6, 3, 5, 4, 6}$，背包的容量为10，根据动态规划函数，用一个 $(n+1)×(C+1)$的二维表 $V$， $V[i][j]$表示把前i个物品装入容量为j的背包中获得的最大价值。以物品数为阶段进行计算：
$eg.第三阶段(i=3)的子问题\\ 容量j=8>6=\omega_3可以装入,对应于情况2此时:\\max\{V[2][8]=9,V[2][2]+5=11\}$

以此类推，计算出每一阶段的，最后取得最大值如下表。

最长公共子序列问题

1.问题定义

• 子序列(递增，非连续性)：对给定序列 $X=(x_1, x_2,…, x_m)$和序列 $Z=(z_1, z_2,…, z_k)$, $Z$是 $X$的子序列当且仅当存在一个严格递增下标序列 $(i_1, i_2,…, i_k)$，使得对于所有 $j=1, 2, …, k$，有 $z_j=x_{ij}(1≤ij≤m)$。
• 子序列(公共):另一个序列Z既是X的子序列又是Y的子序列即为公共子序列。

2.例题

例：序列 $X=(a, b, c, b, d, b)$， $Y=(a, c, b, b, a, b, d, b, b)$，建立两个
$(m+1)×(n+1)$的二维表 $L$和表 $S$，分别存放搜索过程中得到的子序列的长度和状态。先初始化第一行第一列，以每行（或列）为一个阶段，向后递推：最后字符相等，左上角加1填入，否则上方和左方的取大填入.

.引入方程

$L[i][j]$表示子序列 $X_i$和 $Y_j$的最长公共子序列的长度，可得如下动态规划函数：
$L[0][0]=L[i][0]=L[0][j]=0(1≤i≤m,1≤j≤n)$

$L[i][j]= \left \{ \begin{aligned} &L[i-1][j-1]+1&x_i=y_i,i>1,j>1\\ &max \{L[i][j-1],L[i-1][j]\}&x_i\not= y_i,i>1,j>1 \end{aligned} \right.$

• 填数字的方法：
  $\left \{ \begin{aligned} &看左上，左\not =右取大值\\ &看左上，左=上看横纵\left \{ \begin{aligned} &+1(横=纵)\\ &不变(横\not=纵) \end{aligned} \right. \end{aligned} \right.$
  
• 找最长子串的方法：
  $\left \{ \begin{aligned} &看左上\left \{ \begin{aligned} &左移(左=中)\\ &上移(上=中) \end{aligned} \right.\\ &看左上，左\not=中\&\&上\not=中：对角线移 \end{aligned} \right.$

查找问题中的动态规划法

最优二叉查找树(查找过程中动态生成表)

二叉查找树

根节点的值大于其左子树中任意一个节点的值，小于其右子树中任意一节点的值

2.问题定义

• 二叉查找树定义
  将由 $\{r_1, r_2, …, r_n\}$构成的二叉查找树记为 $T(1, n)$，其中 $r_k(1≤k≤n)$ 是 $T(1, n)$的根结点，则其左子树 $T(1, k-1)$由 $\{r_1 , …, r_{k-1}\}$构成，其右子树 $T(k+1, n)$由 $\{r_{k+1}, …, r_n\}$构成。
  
• 最优解方程：设 ${r_1, r_2, …, r_n}$是 $n$个记录的集合，其查找概率分别是 ${p_1, p_2, …, p_n}$，最优二叉查找树是以这 $n$个记录构成的二叉查找树中具有最少平均比较次数的二叉查找树，即：
  $\sum_{i=1}^np_i*c_i$

最小，其中 $p_i$是记录 $r_i$的查找概率， $c_i$是在二叉查找树中查找 $r_i$的比较次数。

3.例题

放个小图，自己理会：

4.动态规划函数

$T(i, j)$：记录 ${r_i, …, r_j}(1≤i≤j≤n)$构成的二叉查找树
$r_k$：二叉查找树的根结点
$C(i, j)$： $T(i, j)$这棵树的平均比较次数
方程如下：
$\left \{ \begin{aligned} &C(i,j)=min_{i \leq k \leq j } \{C(i,k-1)+C(k+ 1,j)+\sum_{s =i}^jp_s\}\\ &C(i, i-1)=0 (1≤i≤n+1) \\ &C(i, i)=p_i (1≤i≤n) \end{aligned} \right.$

例题

例如，集合{A, B, C, D}的查找概率是{0.1, 0.2, 0.4, 0.3}，二维表C和R的初始情况如图所示：

近似串匹配问题

未完…待续…

超链接

更多相关内容：
TSP(旅行者问题)——动态规划详解
0/1背包问题
最长公共子序列问题，手把手演示求动态规划数组!
动态查找表（二叉排序树）
一个排版HTML的小常识：
CSDN博客排版技巧