梯度算法推导 (机器学习必读02)

要点：

1 梯度下降核心在与求某个点的导数，然后根据学习率设定的步长 * 导数计算出下一个值，然后计算出下一个点的导数。

一无约束最优化问题

无约束最优化问题（unconstrained optimization problem）指的是从一个问题的所有可能的备选方案中，选择出依某种指标来说是最优的解决方案。从数学上说，最优化是研究在一个给定的集合S上泛函 $J(\theta)$ 的极小化或极大化问题：广义上，最优化包括数学规划、图和网络、组合最优化、库存论、决策论、排队论、最优控制等。狭义上，最优化仅指数学规划。

1.1 梯度下降

梯度下降法(Gradient Descent)是一个算法，但不是像多元线性回归那样是一个具体做回归任务的算法，而是一个非常通用的优化算法来帮助一些机器学习算法（都是无约束最优化问题）求解出最优解，所谓的通用就是很多机器学习算法都是用梯度下降，甚至深度学习也是用它来求解最优解。所有优化算法的目的都是期望以最快的速度把模型参数θ求解出来，梯度下降法就是一种经典常用的优化算法。

之前利用正规方程求解的 θ 是最优解的原因是 MSE 这个损失函数是凸函数。但是，机器学习的损失函数并非都是凸函数，设置导数为 0 会得到很多个极值，不能确定唯一解。

之前我们令导数为 0，反过来求解最低点 θ 是多少，而梯度下降法是一点点去逼近最优解!

1.2 梯度下降公式

梯度下降核心在与求某个点的倒数，然后根据学习率设定的步长 * 导数计算出下一个值，然后计算出下一个点的倒数。

1.3 学习率

根据我们上面讲的梯度下降公式，我们知道 $\eta$ 是学习率，设置大的学习率 $w_j$ 每次调整的幅度就大，设置小的学习率 $w_j$ 每次调整的幅度就小，然而如果步子迈的太大也会有问题，俗话说步子大了容易扯着蛋！学习率大，可能一下子迈过了，到另一边去了（从曲线左半边跳到右半边），继续梯度下降又迈回来，使得来来回回震荡。步子太小呢，就像蜗牛一步步往前挪，也会使得整体迭代次数增加。

学习率的设置是门一门学问，一般我们会把它设置成一个比较小的正整数，0.1、0.01、0.001、0.0001，都是常见的设定数值（然后根据情况调整）。一般情况下学习率在整体迭代过程中是不变，但是也可以设置成随着迭代次数增多学习率逐渐变小，因为越靠近山谷我们就可以步子迈小点，可以更精准的走入最低点，同时防止走过。还有一些深度学习的优化算法会自己控制调整学习率这个值，后面学习过程中这些策略在讲解代码中我们会一一讲到。

1.4 随机取初始值

若随机初始化，算法从左侧起步，那么会收敛到一个局部最小值，而不是全局最小值；
若随机初始化，算法从右侧起步，那么需要经过很长时间才能越过Plateau（函数停滞带，梯度很小），如果停下得太早，则永远达不到全局最小值；

而线性回归的 模型MSE损失函数 恰好是个凸函数，凸函数保证了只有一个全局最小值，其次是个连续函数，斜率不会发生陡峭的变化，因此即便是乱走，梯度下降都可以趋近全局最小值。

1.5 梯度下降步骤

梯度下降流程就是“猜”正确答案的过程:

1、“瞎蒙”，Random 随机数生成 $\theta$ ，随机生成一组数值 $w_0, w_1.......w_n$ ，期望 $\mu$ 为 0 方差 $\sigma$ 为 1 的正太分布数据。
2、求梯度 g ，梯度代表曲线某点上的切线的斜率，沿着切线往下就相当于沿着坡度最陡峭的方向下降
3、if g < 0, $\theta$ 变大，if g > 0, $\theta$ 变小。 # 根据斜率计算下一个值
4、判断是否收敛，如果收敛跳出迭代，如果没有达到收敛，回第 2 步再次执行2~4步。收敛的判断标准是：随着迭代进行损失函数Loss，变化非常微小甚至不再改变，即认为达到收敛， # 判断斜率大小是否达到目标值。

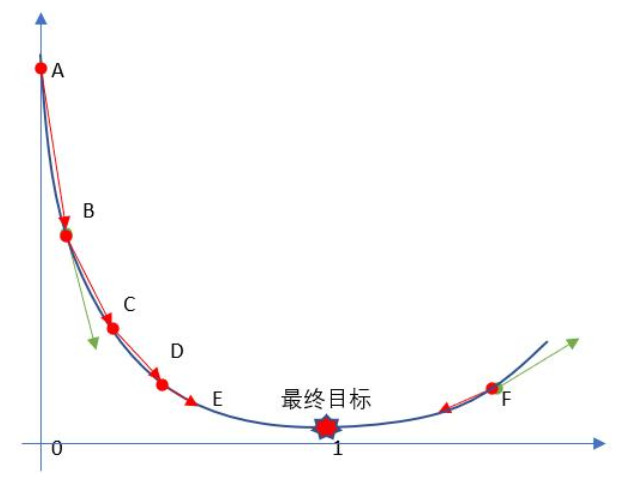
二代码模拟梯度下降

2.1 定义求解函数

import numpy as np
import matplotlib.pyplot as plt

# 求解函数
f = lambda x: (x - 3.5) ** 2 - 4.5 * x + 10 
# 导函数
d = lambda x: 2 * (x - 3.5) - 4.5
# 定义学习率，步幅
step = 0.1

2.2 随机取初始值

# 随机取初始值
last_x = np.random.randint(0,12,size = 1)[0]
# 求变化值
dif = d(last_x)
# 记录上一步的值，首先让两个值有差异
x = last_x - dif*step
# 上一个值:11,斜率：10.5，实时值x:9.95
print(f'上一个值:{last_x},斜率：{dif}，实时值x:{x}')

2.3 迭代循环

# 精确率，真实计算，都是有误差，自己定义 # 判断是否收敛
precision = 1e-4
x_ = [x]
print(f'开始迭代计算，最终误差：{precision}')
num = 0   # 记录迭代次数
while True:
    num += 1
    # 退出条件，精确度，满足了
    if np.abs(x - last_x) < precision:
        break   
    # 更新
    last_x = x
    x -= step*d(x) # 更新，减法：最小值
    x_.append(x)
    print(f'------>迭代次数：{num:2}，斜率：{d(last_x):.5f}，差值：
          {(x-last_x):.5f}，上一个值：{last_x:.5f}，重算后值：{x:.5f}')

2.4 可视化计算过程

# 数据可视化
plt.rcParams['font.family'] = 'Kaiti'
plt.figure(figsize=(9,6))
x = np.linspace(5.75 - 5, 5.75 + 5, 100)
y = f(x)
plt.plot(x,y,color = 'green')
plt.title('梯度下降',size = 24,pad = 15)
x_ = np.array(x_)
y_ = f(x_)
plt.scatter(x_, y_,color = 'red')

注意：

梯度下降存在一定误差，不是完美解~
在误差允许的范围内，梯度下降所求得的机器学习模型，是堪用的！
梯度下降的步幅step，不能太大，俗话说步子不能迈的太大！
精确度，可以根据实际情况调整
while True循环里面，持续进行梯度下降
while 循环退出条件是：x更新之后和上一次相差绝对值小于特定精确度！