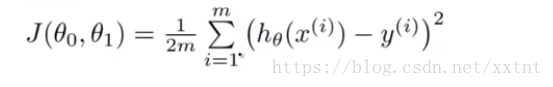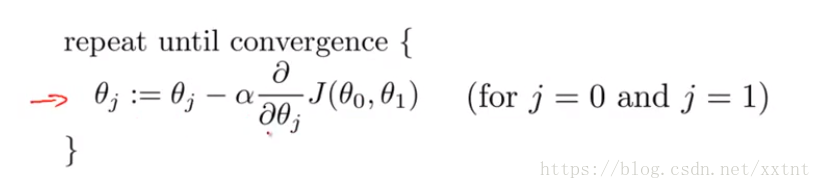建议记住的实用符号
| 符号 |
含义 |
| m |
样本数目 |
| x |
输入变量 |
| y |
输出变量/目标变量 |
| (x,y) |
训练样本 |
| (x^(i),y^(i)) |
第i个训练样本 |
| h |
假设的函数( h(x) = y ) |
H函数:
hθ(x) = θ0 + θ1*x( h(x) ) 【单变量线性回归模型】
备注:常用希腊字母
| Α α:阿尔法 Alpha |
Β β:贝塔 Beta |
Γ γ:伽玛 Gamma |
Δ δ:德尔塔 Delte |
| Ε ε:艾普西龙 Epsilon |
Ζ ζ :捷塔 Zeta |
Ε η:依塔 Eta |
Θ θ:西塔 Theta |
| Ι ι:艾欧塔 Iota |
Κ κ:喀帕 Kappa |
∧ λ:拉姆达 Lambda |
Μ μ:缪 Mu |
| Ν ν:拗 Nu |
Ξ ξ:克西 Xi |
Ο ο:欧麦克轮 Omicron |
∏ π:派 Pi |
| Ρ ρ:柔 Rho |
∑ σ:西格玛 Sigma |
Τ τ:套 Tau |
Υ υ:宇普西龙 Upsilon |
| Φ φ:fai Phi |
Χ χ:器 Chi |
Ψ ψ:普赛 Psi |
Ω ω:欧米伽 Omega |
1、已知训练集
2、计算出恰当的θ0和θ1的值,使之得到的结果最接近已知的训练集( hθ(x) = θ0 + θ1*x ),尽可能的让其方差的1/2M的值最小。
代价函数(平方误差函数): J(θ0, θ1) = 1/(2m)∑(h(x^(i) – y ^(i))²
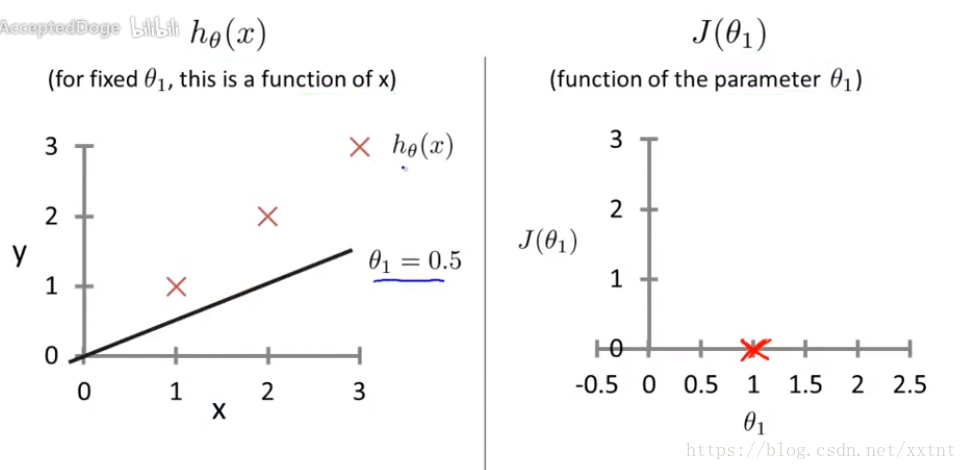
代价函数和假设函数
左边是假设函数:假设函数是为了确定θ1的值,是一个关于x的函数
右边是代价函数:是一个关于θ1的函数,求得不同θ1的情况下,代价函数的值(即误差的大小)。
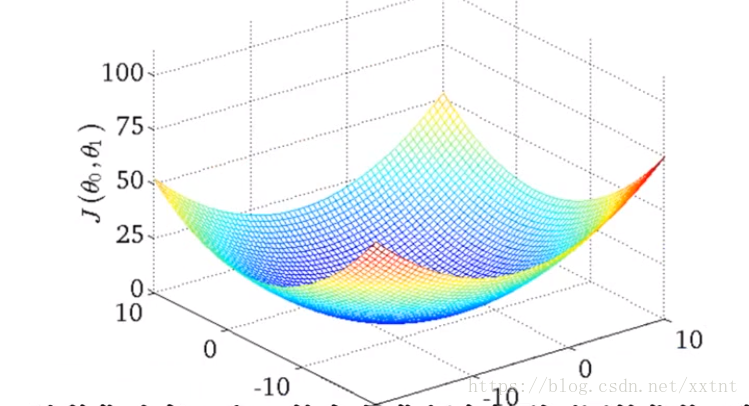
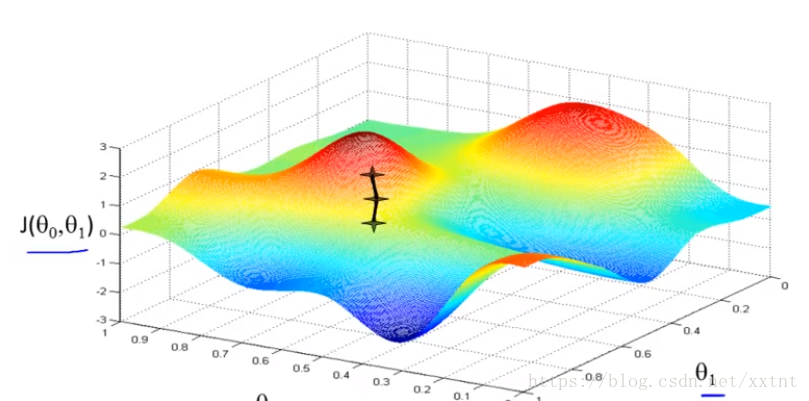
同时考虑θ0和θ1所绘制的代价函数,其中点最低的部分则是我们理想的假设函数。
求θ0和θ1的算法
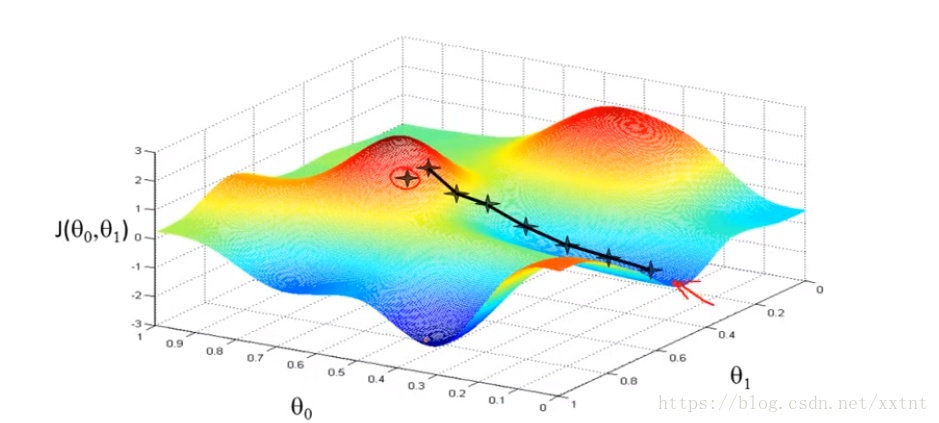
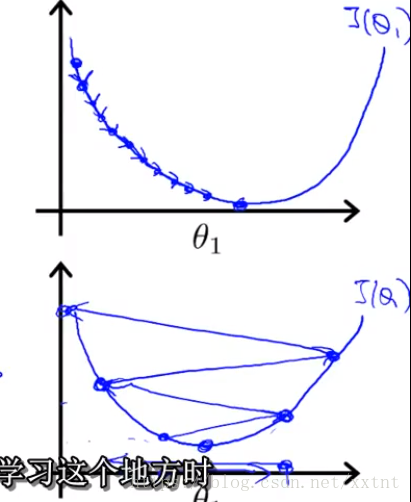
【梯度下降】将代价函数的值(就房价问题的训练集)进行可视化,想象如果你在山顶,以最快的速度走到山脚(即快速找到θ0和θ1恰当的值,使代价函数的值在某个较小的值的范围内)
梯度下降函数会给我们返回局部最优解,不同的初始值也许到达的点不同(即对θ0和θ1刚开始赋值不同,得到的最终值也会不一样)
- 给θ0和θ1设置初始值
- 通过梯度下降算法得到局部最优解
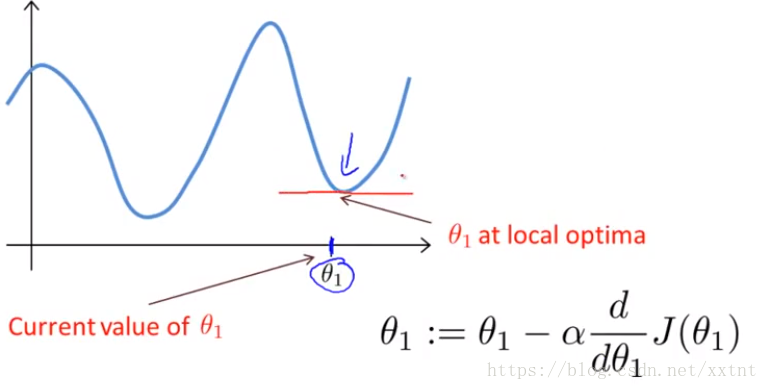
梯度下降算法
解析:
:= 赋值运算符(对的就是一个冒号加等号)
= 类似于C语言中的==(不知道老师使用的是哪里的语法,matlab不是这样的 [○・`Д´・ ○])
α 学习速率,是一个数字(控制下山的距离,即控制θ值变化的大小,其大小与α成正比,α>0 )
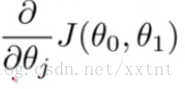
每一次都会重新对θ0和θ1重新赋值(同时更新,即两个微分中的θ0和θ1都是它们原来的值)

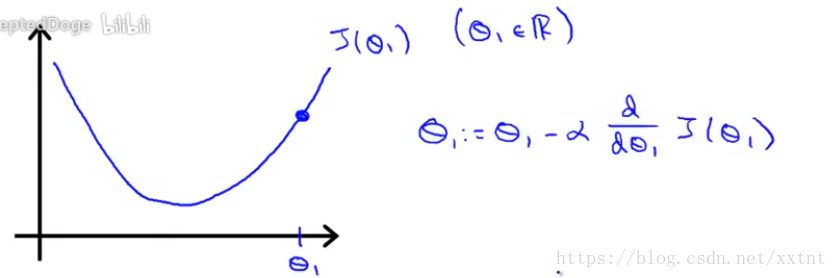
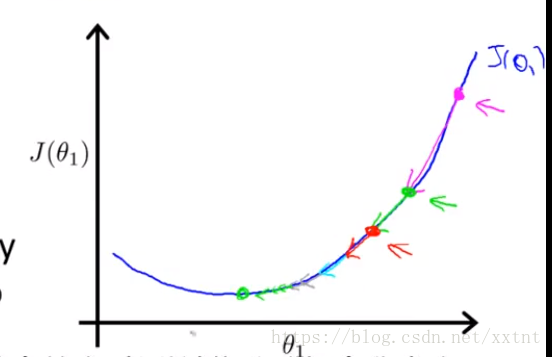
第二个它的导数值为正数,因为y值随着x值的升高而升高
- 由于代价函数的值恒大于零(有其表达式可知),所以我们可以很容易得到,无论θ所在的斜率是正是负,它永远是朝中J(θ)值降低的方向移动。因此,导数项的意义是为了保证随着θ的变化是朝着代价函数的值下降的那个方向。
- α的值的大小也会影响到我们最终的结果,α值太小,会导致下降的比较慢,α太多,有可能会导致越过最低点。
如下图
- 代价函数和导数的值同样起到对下降距离的调节作用,随着代价函数的值逐步降低,下降的距离逐渐变小,也就如下图所示。
下降算法的之所以存在局部最优解,与其算法有关。当到达一个位置θ0和θ1的偏导数都为0时,θ0和θ1将不再改变,也就是说,会出现求得的值为极小值而不是最小值的情况。(如果存在θ0和θ1都为0的多个点)
这也就是我们的梯度下降,其中圈着的部分,分别是各自偏导数求出的结果