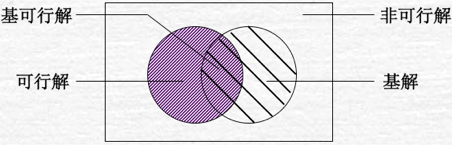
整数规划——第二章 线性规划

整数规划——第二章 线性规划

2.1 凸分析初步

2.1.1 凸集和分离定理

定义2.1 设集合 $C\subseteq {\mathbb{R}}^n$，如果对任意 $x,y\in C$ 和 $\lambda \in [0,1]$，有
$$\lambda x+(1-\lambda )y\in C,$$

则称 $C$ 为凸集。

在凸几何中，凸集(convex set)是在凸组合下闭合的仿射空间的子集。更具体地说，在欧氏空间中，凸集是对于集合内的每一对点，连接该对点的直线段上的每个点也在该集合内。例如，立方体是凸集，但是任何中空的或具有凹痕的例如月牙形都不是凸集。

定理2.1 设$C\subseteq {\mathbb{R}}^n$ 为非空闭凸集，$y\in {\mathbb{R}}^n,y\notin C$，则

1. 存在唯一的点 $\overline{x}\in C$，使
   ∣ ∣ x ‾ − y ∣ ∣ = inf ⁡ { ∣ ∣ x − y ∣ ∣   ∣   x ∈ C } ||\overline{x}-y|| = \inf \{||x-y||\ |\ x\in C \} ∣∣x−y∣∣=inf{ ∣∣x−y∣∣ ∣ x∈C}

   在数学符号中，“inf"代表"infimum”，这是数学分析和集合论中的一个概念。某一集合的infimum是该集合的下界中最大的实数。简单来说，它是小于等于该集合中所有数的最小实数。

   该定理表明非空闭凸集中存在与给定点 $y$ 最近的点，并且这个点是唯一的。

2. $\overline{x}\in C$ 为点 $y$ 到集合 $C$ 的最近点充要条件是
   $$(x-\overline{x}{)}^T(\overline{x}-y)\ge 0,\forall x\in C\text{\hspace{1em}(2.1)}$$

定理2.2 凸集分离定理 设$C\subseteq {\mathbb{R}}^n$ 为非空闭凸集，$y\in {\mathbb{R}}^n,y\notin C$，则存在非零向量$a\in R^n$ 和数 $\beta$ 使得
$$a^{\text{T}}x\le \beta <a^{\text{T}}y,\forall x\in C$$
具体来说：

• $a$ 是一个非零向量，它定义了一个超平面。
• $\beta$ 是一个实数，它表示超平面在 $a^{\text{T}}x$ 方向上的偏移量。
• 对于集合 $C$ 中的所有点 $x$，它们都位于这个超平面的一侧，并且超平面分离了点 $y$ 和集合 $C$ 。

这个定理直观地说明了在凸集 $C$ 和点 $y$ 之间存在一个超平面，将点 $y$ 与集合 $C$ 完全分开，即点 $y$ 在超平面的一侧，而集合 在另一侧 $C$ 。这个超平面可以看作是一条线（$n=2$ ）或者一个平面（$n=3$）或者更高维空间中的超平面。

2.1.2 多面体基本知识

定义2.2 若 $S\subseteq R^n$ 是有限多个半空间之交，则称 $S$ 为多面体，即 S = { x ∈ R n ∣ a i T ≤ b i ,   i = 1 , . . . , m } S=\{x\in \R^n |a^T_i \le b_i,\ i=1,...,m\} S={ x∈Rn∣aiT​≤bi​, i=1,...,m}，这里 $a\in {\mathbb{R}}^n,ai\ne 0，b_i\in \mathbb{R}$

容易看出，多面体都是闭凸集。设$A\in {\mathbb{R}}^{m\times n},b\in R^m$,下面的集合都是多面体：
S = { x ∈ R n ∣ A x ≤ b } , S = { x ∈ R n ∣ A x = b ,   x ≥ 0 } , S = { x ∈ R n ∣ A x ≤ b ,   x ≥ 0 } . \begin{aligned} &S=\{x\in \R^n| Ax\le b\},\\ &S=\{x\in \R^n| Ax= b,\ x\ge 0\},\\ &S=\{x\in \R^n| Ax\le b,\ x\ge 0\}. \end{aligned} ​S={ x∈Rn∣Ax≤b},S={ x∈Rn∣Ax=b, x≥0},S={ x∈Rn∣Ax≤b, x≥0}.​

多面体为一系列的（有限个）线性等式和不等式的解集。

半空间是由超平面和它在一个特定侧面的所有点构成的区域

定义2.3 设$S\subseteq {\mathbb{R}}^n$是非空凸集，$x\in S$。若对任意$\lambda \in (0,1)$和 $x_1,x_2\in S$,$x=\lambda x_1十(1一\lambda )x_2$可推出 $x_1=x_2=x$ ,则称 $x$ 为 $S$ 的顶点。

即若 $C$ 中不存在任何两个不同的点，使 $x$ 成为这两个点连线上的一个点，则 $x$ 为顶点。

定义2.4 设$S\subseteq {\mathbb{R}}^n$是非空凸集，$d\in {\mathbb{R}}^n$。若对任意 $x\in S$ 和 $\lambda \ge 0$ 都有$x+\lambda d\in S$,则称 $d$ 为 $S$ 的一个方向。若对任意${\lambda }_1,{\lambda }_2>0$和 $S$ 的方向 $d_1,d_2$ ，由$d={\lambda }_1{d}_1+{\lambda }_2{d}_2$可推出 $d_1=\alpha d_2$，其中 $\alpha >0$，则称 $d$ 为 $S$ 的极方向。(若 $S$ 的方向 $d$ 不能表示为该集合的两个不同方向的正的线性组合，则称 $d$ 为 $S$ 的极方向。)

直观上来说，极方向可以看作是在凸集 $S$ 的边界点 $x_0$ 处的“最远延伸方向”。在极方向上，你可以在该方向上无限远地向外延伸，而仍然保持在凸集 $S$ 内部。

定理2.3 设 S = { x ∈ R n ∣ A x = b , x ≥ 0 } S=\{x\in \R^n|Ax=b,x\ge0\} S={ x∈Rn∣Ax=b,x≥0}，其中 $A$ 行满秩，则 $x\in S$ 是 $S$ 的顶点的充要条件为$x$ 可以表示为 $ x = \left( \begin{aligned} &B^{-1}b \cr &0 \end{aligned} \right)$，其中 $A=(B,N)$，$B$ 可逆且$B^{-1}b\ge 0$

定理2.4 设 S = { x ∈ R n ∣ A x = b , x ≥ 0 } S=\{x\in \R^n|Ax=b,x\ge 0\} S={ x∈Rn∣Ax=b,x≥0} 非空，其中 $A$ 行满秩，则$S$ 至少有一个顶点。

2.2 线性规划与原始单纯形法

考虑线性规划（Linear Programming，LP）的标准形式：
( L P ) min ⁡ { c T x ∣ A x = b , x ≥ 0 } (LP)\quad \min\{c^{\text{T}}x|Ax = b,x\ge 0\} (LP)min{ cTx∣Ax=b,x≥0}
此处 $A\in R^{m\times n}$，$A$ 行满秩，设 S = { x ∈ R n ∣ A x = b , x ≥ 0 } S=\{x\in \R^n | Ax = b, x\ge 0\} S={ x∈Rn∣Ax=b,x≥0}，称$S$ 为 （LP) 的可行域。

在线性方程组求解中，行满秩矩阵往往具有唯一解。

定理 2.7 （线性规划基本定理）设线性规划可行域 $S$ 非空， $S$ 的顶点为 $x_1,...,x_k$ ，极方向为 $d_i,...,d_l$，则(LP)有有限最优解的充要条件为 $c^T{d}_i\ge 0，i=1,...,l$。若（LP)有有限最优解，则(LP）必在其中一个顶点 $x_j$ 上达到最优.

定义2.5 考虑线性规划（LP）的可行域 $S$ ，设$A=(B,N)$ ，其中 $B$ 可逆，则称 $B$ 为 $A$ 的一个基，$x=\left(\begin{array}{rl}& x_B\\ & x_N\end{array}\right)=\left(\begin{array}{rl}& B^{-1}b\\ & 0\end{array}\right)$为 $Ax=b$ 的基本解，$x_B$ 称为基变量，$x_N$ 为非基变量。若 $B^{-1}b\ge 0$，则称 $B$ 为原始可行基，$x=\left(\begin{array}{rl}& B^{-1}b\\ & 0\end{array}\right)$ 称为基本可行解。

可知矩阵 $A$ 是 $m\times n$ 的矩阵，这里我们假设 $A$ 是行满秩（即每行等式都是有意义的），且 $m<n$ ，则 $A$ 的基向量有 $m$ 个。我们把A按列重新排列，表示成$A=(B,N)$，其中 $B$ 由 $m$ 个基向量表示，$N$ 由其他 $n-m$ 个非基向量组成。相应的，$x$也可以表示成基变量和非基变量的组合 $x=\left(\begin{array}{rl}& x_B\\ & x_N\end{array}\right)$，目标函数表示为 $c_B^T{x}_B+c_N^T{x}_N$ 。对于等式 $Ax=b$ ，可以表示成 $B{x}_B+N{x}_N=b$ 。

非基变量$x_N$ 全部取值为0得到的解称之为基解，基解的个数最多为 $C_n^m$，若 $x>0$，则称之为基本可行解。

假设2.1（非退化假设） 对任意基本可行解$x=\left(\begin{array}{rl}& B^{-1}b\\ & 0\end{array}\right)$，都有 $B^{-1}b>0$

性质2.1 线性规划的可行域S的顶点和基本可行解一一对应，线性规划若有有限最优解，则一定存在基本可行解是最优解。

上述定理和性质表明，我们只需在可行域的顶点中寻找线性规划的最优解.

单纯形法

单纯形：n维空间内有n+1个顶点的多面体

算法2.1 原始单纯形算法

步0：计算初始基本可行基 $B$ 和对应的基本可行解 $x=\left(\begin{array}{rl}& B^{-1}b\\ & 0\end{array}\right)$。

步1：如果 $r_N=c_N^T-c_B^T{B}^{-1}N\ge 0$，停止，当前基本可行解 $x$ 是最优解，否则，转步2.

步2：选取 $j$ 满足 $c_j-c_B^T{B}^{-1}{a}_j<0$，若 ${\overline{a}}_j=B^{-1}{a}_j\le 0$ 停止，原问题无界；否则，转步3.

步3：由 下式 计算 $\lambda$ ，令 $x:=x+\lambda d_j$，其中 $d_j=\left(\begin{array}{rl}& -B^{-1}{a}_j\\ & e_j\end{array}\right)$，转步1
$$\lambda =\min \left\{\frac{{\overline{b}}_i}{{\overline{a}}_{ij}}|{\overline{a}}_{ij}>0\right\}=\frac{{\overline{b}}_r}{{\overline{a}}_{rj}}\ge 0$$

内在思路：首先我们可以确定一组基，然后通过这一组基求出基可行解。这是0-1步的工作，当我们求出了基可行解之后，我们还需要判断它是不是最优解，这就是2步的工作最优性检验。假设我们检验后知道，所求的解是最优解，那运气确实很好，倘若不是也没有关系，我们就进入3步换基变量。这样就可以求出新的一组基可行解，再进行最优性检测，直到找到最优解为止

单纯形法就是在任意的n维空间内的单纯形上，从一个顶点移动到另一个更好的顶点。直到找不到更好的顶点时，就说明已经达到最优解。

定理2.8 在非退化假设下，原始单纯形算法有限步终止，或找到(LP)的一个最优解，或判断出(LP)无界。

可以用表格的形式表达上述算法，设 $b\ge 0$，设初始可行基为 $B$ ，$A=(B,N)$，则单纯形方法一次迭代过程可以在下列表格上进行：

“rhs” 是"right-hand side"（右侧常数）的缩写

例2.1 利用单纯形算法求解下列线性规划
$$\begin{array}{rl}& \min -7x_1-2x_2\\ & s.t.-x_1+2x_2+x_3=4,\\ & 5x_1+x_2+x_4=20,\\ & 2x_1+2x_2-x_5=7,\\ & x\ge 0\end{array}$$
初始单纯形表如下：

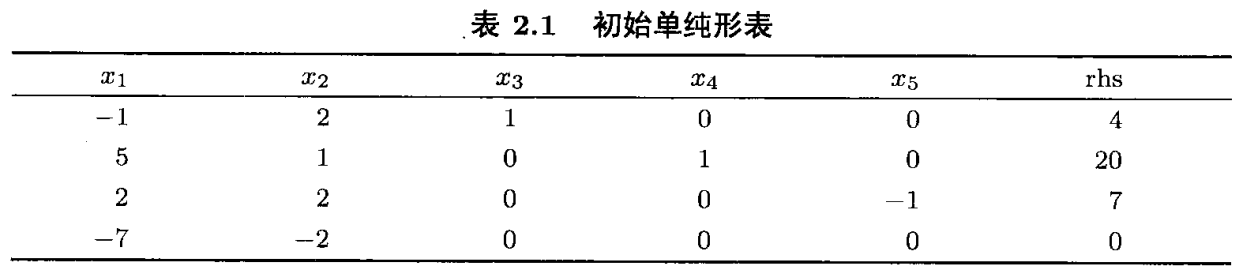
第1次迭代。选择初始基 $B=(a_1,a_3,a_4)$，以 $x_B=(x_1,x_3,x_4{)}^T$ 为基变量的单纯形表见下表，其对应的初始基本可行解为$x_B=(x_1,x_3,x_4{)}^T=(3\frac{1}{2},7\frac{1}{2},2\frac{1}{2})，x_N=(x_2,x_4{)}^T=(0,0{)}^T$

第2次迭代，因$-\frac{7}{2}<0$，选择 $x_5$ 为进基变量，计算$\lambda =\frac{2\frac{1}{2}}{2\frac{1}{2}}=1$，故 $x_4$ 是离基变量，新的基变量为$x_B=(x_1,x_3,x_5)$。新的单纯形表为表2.3：

第3次迭代，选择 $x_2$ 为进基变量，计算$\min \left\{\frac{8}{11/5},\frac{4}{1/5}\right\}$。故 $x_3$ 是离基变量，新的单纯形表2.4，由于$r_N=(\frac{3}{11},\frac{6}{11})\ge 0$，当前基本可行解 $x=(\frac{36}{11},\frac{40}{11},0,0,\frac{75}{11}{)}^T$ 是线性规划的最优解，最优值为 $-30\frac{2}{11}$。

在上述单纯形算法中，我们要求问题有一个初始基本可行解，下面讨论如何在一般情况下求问题的初始可行解。考虑标准形式的线性规划：
( L P ) min ⁡ { c T x ∣ A x = b , x ≥ 0 } (LP)\quad \min\{c^{\text{T}}x|Ax = b,x\ge 0\} (LP)min{ cTx∣Ax=b,x≥0}
这里 $b\ge 0$，引入人工变量 $y\in {\mathbb{R}}_{+}^m$，考虑如下线性规划：
( L P a ) min ⁡ { e T y ∣ A x + y = b , x ≥ 0 , y ≥ 0 } (LP^a)\quad \min\{e^{\text{T}}y|Ax+y = b,x\ge 0,y\ge 0\} (LPa)min{ eTy∣Ax+y=b,x≥0,y≥0}
下列结论显然成立：

• 线性规划（$L{P}^a$）可行且有可行解 $(x,y)=(0,b)$，其最优值大于或等于0.
• 线性规划$(LP)$有可行解当且仅当$(L{P}^a)$的最优值为0。特别地，若$(L{P}^a)$的最优解中人工变量 $y_i(i=1,...,m)$ 都是非基变量，则该最优解也是 $(LP)$ 的一个基本可行解

利用上述方法求初始基本可行解称为阶段Ⅰ，而获得初始可行解后求解原问题的最优解成为阶段Ⅱ。整个求解过程称为两阶段方法。

例2.1（续）：用阶段Ⅰ求解初始可行解，可以构造如下问题：
$$\begin{array}{rl}& \min y_1+y_2+y_3,\\ & s.t.-x_1+2x_2+x_3+y_1=4,\\ & 5x_1+x_2+x_4+y_2=20,\\ & 2x_1+2x_2-x_5+y_3=7,\\ & x\ge 0,y\ge 0\end{array}$$
注意到 $x_3$ 和 $x_4$ 可以看作是松弛变量，故人工变量 $y_1$ 和 $y_2$ 是多余的，只需引进 $y_3$ 为人工变量。故阶段Ⅰ的线性规划问题可简化为：
$$\begin{array}{rl}& \min y_3,\\ & s.t.-x_1+2x_2+x_3=4,\\ & 5x_1+x_2+x_4=20,\\ & 2x_1+2x_2-x_5+y_3=7,\\ & x\ge 0,y_3\ge 0\end{array}$$
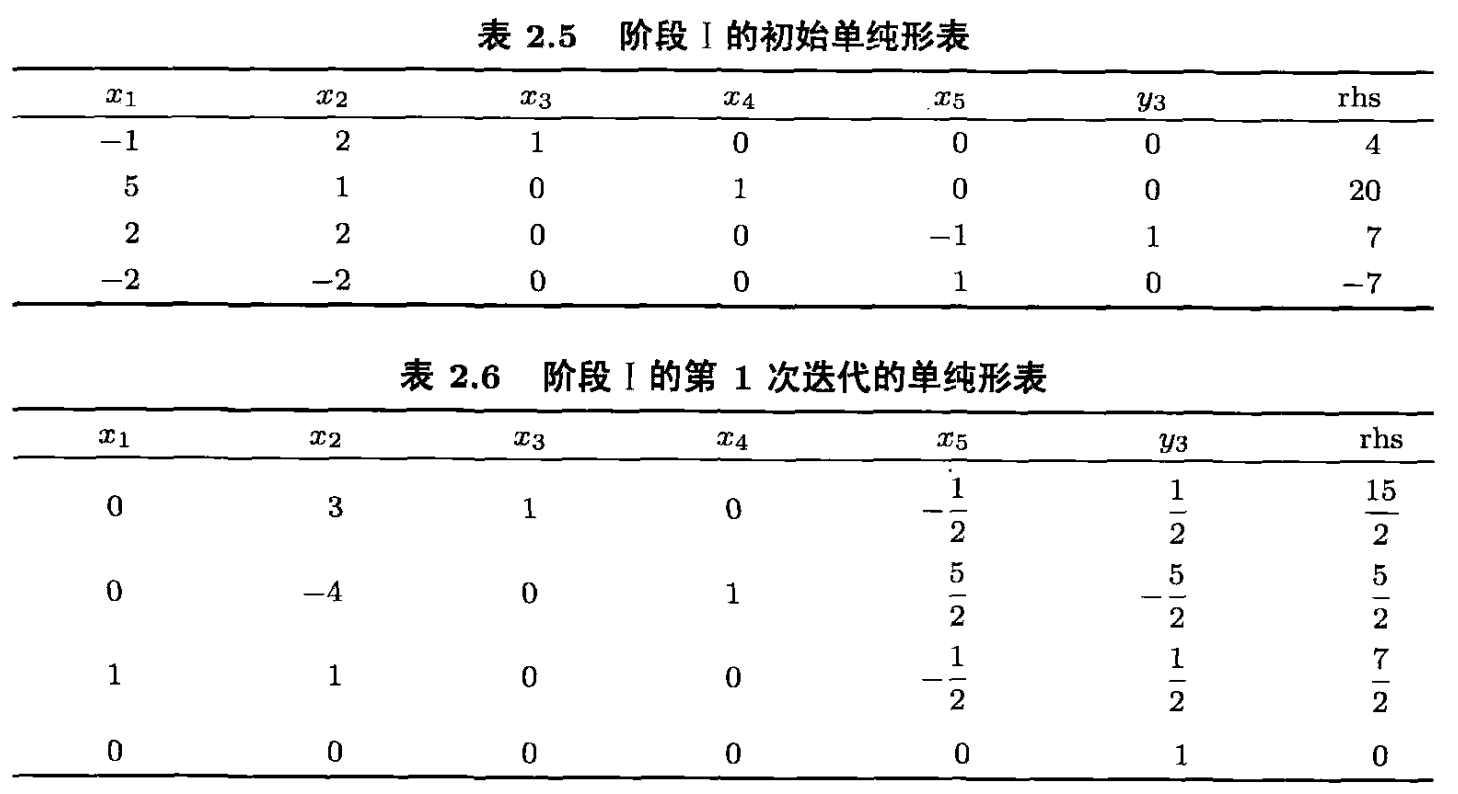
显然，初始基变量为$x_B=(x_3,x_4,y_3{)}^T$，对应的单纯形表见表2.5。选择 $x_1$ 进基，$\lambda =\min (\frac{20}{5},\frac{7}{2})$，故 $y_3$ 出基，新的基变量为 $x_B=(x_1,x_3,y_4{)}^T$,对应的单纯形表见表2.6。这就得到初始基本可行解 $x=(\frac{7}{2},0,\frac{15}{2},\frac{5}{2},0{)}^T$。在单纯形表2.6中删除对应的列就得到阶段Ⅱ的初始单纯形表

2.3 线性规划对偶与对偶单纯形法

考虑下列线性规划问题：
( P ) max ⁡ { c T x ∣ A x ≤ b , x ∈ R + n } (\text{P})\quad \max\{c^{\text{T}} x|Ax\le b,x\in \R^n_{+}\} (P)max{ cTx∣Ax≤b,x∈R+n​}
此处 $A\in {\mathbb{R}}^{m\times n}$，$A$ 行满秩，§ 的对偶问题定义为：
( D ) min ⁡ { b T u ∣ A T u ≥ c , u ∈ R + m } (\text{D})\quad \min\{b^{\text{T}} u|A^{\text{T}}u\ge c,u\in \R^m_{+}\} (D)min{ bTu∣ATu≥c,u∈R+m​}
这里 $R_{+}^m$ 表示 $m$ 维非负向量集合。容易验证，标准形式的线性规划
( LP ) min ⁡ { c T x ∣ A x = b , x ∈ R + n } (\text{LP})\quad \min\{c^{\text{T}} x|Ax= b,x\in \R^n_{+}\} (LP)min{ cTx∣Ax=b,x∈R+n​}
的对偶问题为：
( LD ) max ⁡ { b T u ∣ A T u ≤ c , u ∈ R + m } (\text{LD})\quad \max\{b^{\text{T}} u|A^{\text{T}}u\le c,u\in \R^m_{+}\} (LD)max{ bTu∣ATu≤c,u∈R+m​}
定理2.9 (弱对偶性) 设 $x$ 是 (LP) 的可行解，$u$ 是 (LD) 的可行解，则 $c^{\text{T}}x\ge b^{\text{T}}u$

推论2.1 若$v(LP)=-\infty$，则(LD)不可行；反之若$v(LD)=+\infty$，则(LP)不可行。即当原始线性规划问题(LP)是无界的，对偶问题(LD)一定不可行。

推论2.2 （互补松弛条件）设 $x$ 和 $u$ 分别是(LP)和(LD)的可行解，令 $s=c-A^{\text{T}}u$，则 $x$ 和 $u$ 分别是(LP)和(LD)的最优解的充要条件是 $s_i{x}_i=0,i=1,...,n$。

定理2.10 （强对偶性）设（LP）或（LD）可行且最优解有限，则 $v(LP)=v(LD)$。

即如果原始问题(LP)和对偶问题(LD)中至少存在一个可行解，并且两个问题都有有限的最优解，那么它们的最优目标函数值是相等的

推论2.3 对线性规划(LP)和它的对偶问题(LD),只有下面四种情况之一发生：

1. (LP)和(LD)都有有限最优解且 $v(LP)=v(LD)$;
2. $v(LP)=-\infty$,(LD)不可行；
3. $v(LD)=+\infty$,(LP)不可行；
4. (LP)和(LD)皆不可行.

推论2.4 (Farkas引理) 设$A\in {\mathbb{R}}^{m\times n},c\in {\mathbb{R}}^n$，则下列系统有且仅有一个有解：

1. $Ax\le 0,c^{T}x>0$
2. $A^{T}u=c,u\ge 0$

性质2.2 设 $A=(B,N)$，$B$ 是(LP)的对偶可行基，即 $r_N=c_N^T-c_B^T{B}^{-1}N\ge 0$，令 $\mathcal{B}$ 和 $\mathcal{N}$ 分别表示 $B$ 和 $N$ 的列指标集，记 ${\overline{a}}_j=B^{-1}{a}_j,j\in \mathcal{N},\overline{b}=B^{-1}b$，设${\overline{b}}_s<0$

• 若 ${\overline{a}}_{sj}\ge 0,\forall j\in \mathcal{N}$，则(LP)不可行
• 若存在 $j\in \mathcal{N}$ 使 ${\overline{a}}_{sj}<0$，则有 $B$ 的邻接对偶可行基 $\overline{B}$，其列指标集 B ‾ = B ∪ { t } ∪ { s } \overline{\mathcal{B}}=\mathcal{B}\cup\{t\}\cup\{s\} B=B∪{ t}∪{ s}，这里

t = arg ⁡ min ⁡ j ∈ N { − r j a ‾ s j ∣ a ‾ s j < 0 } (2.14) t=\arg\underset{j\in \mathcal{N}}{\min}\{ -\cfrac{r_j}{\overline{a}_{sj}}|\overline{a}_{sj}<0\}\tag{2.14} t=argj∈Nmin​{ −asj​rj​​∣asj​<0}(2.14)

对偶单纯形算法

• 步0 计算初始对偶可行基 $B$，$A=(B,N)$
• 步1 如果 $\overline{b}=B^{-1}b\ge 0$，则 $x^T=(x_B^T,0)=({\overline{b}}^T,0)\ge 0$是原问题的最优解，否则，转步2
• 步2 选择 $s$ 满足 ${\overline{b}}_s<0$，若 ${\overline{a}}_{sj}\ge 0,\forall j\in \mathcal{N}$，则原问题不可行，否则由（2.14）可得 $t$，令 B : = B ∪ { t } ∪ { s } {\mathcal{B}}:=\mathcal{B}\cup\{t\}\cup\{s\} B:=B∪{ t}∪{ s}，转到步1

例2.1（续）线性规划可写为
$$\begin{array}{rl}& \min -7x_1-2x_2\\ & s.t.-x_1+2x_2+x_3=4,\\ & 5x_1+x_2+x_4=20,\\ & 2x_1+2x_2-x_5=7,\\ & x\ge 0\end{array}$$
使用对偶单纯形法求解：

第1次迭代.选择初始可行基为 $B=(a_2,a_3,a_5)$ .对应的单纯形表为表2.7.因$r_N=r_N=c_N^T-c_B^T{B}^{-1}N=(3,2)\ge 0$，故 $B=(a_2,a_3,a_5)$ 是对偶可行基。而$x_B=\overline{b}=(-36,20,33{)}^T$，故 $B$ 不是原始可行基。

第二次迭代，选择 ${\overline{b}}_3=-36<0$，计算 $\lambda =\min (\frac{3}{11},\frac{3}{2})=\frac{3}{11}$，所以 $x_1$ 进基，$x_3$ 离基，新的对偶可行基为 $B=(a_1,a_2,a_5)$，对应的单纯形表如下。此时对偶可行解为 $x=(\frac{36}{11},\frac{40}{11},0,0,\frac{75}{11})$ 也是原始可行解，从而是原始最优解。

参考文献

1. 整数规划 孙小玲，李瑞 北京，科学出版社 2010
2. 凸集
3. 运筹学S01E02——单纯形法
4. 简单理解线性规划的单纯形算法