功率谱估计(基于Matlab实现)——经典谱估计

周期信号和随机信号的功率谱估计可能是数字信号处理(DSP)最重要的应用领域之一。

频谱分析包含的测量方法种类繁多，可能是无限的，因此文本的目的是对功率谱估计的概念进行简要和基本的介绍和Matlab实现。

一、基本内容

1、频谱

频谱是一种关系，通常由一些参数的幅度或相对值与频率的关系图来表示。每一种物理现象无论是电磁、热、机械、液压还是任何其他系统，都有一个独特的频谱。

在电子学中，这些现象是用信号来处理的，用固定的或变化的电压、电流和功率来表示。这些量通常是在时域中描述的，对每一个时间函数f(t)，可以找到一个等价的频域函数F(w)，它具体描述了生成f(t)所需的频率成分含量(频谱)。

傅里叶分析和傅里叶变换的主题是研究时域和相应的频域表示之间的关系。

函数x(t)的forward Fourier transform，时域到频域的定义：

$F[x(t)] = \int_{-\infty }^{\infty }x(t)\epsilon ^{-jwt}dt=X(w)$

inverse Fourier transform，频域转时域的定义：

$F^{-1}[X(w)] = \frac{1}{2\pi }\int_{-\infty }^{\infty }X(w)\epsilon ^{jwt}dw=X(t)$

2、能量和功率

通过使用傅里叶变换将时域和频域信号函数联系起来。这里重点主要分析信号功率和能量。

帕塞瓦尔定理定理Parseval’s theorem将能量w(t)在时域和频域的表示通过下面的表述联系起来。

$w(t) = \int_{-\infty }^{\infty }{f^{2}}(t)dt=\int_{-\infty }^{\infty }\left | F(f) \right |^{2}df$

*Parseval's theorem表明了信号的能量在时域和频域相等。

*其中f(t)是随时间变化的任意信号，F(f)是在频域中等价的傅里叶变换表示。

该定理简单说明信号f(t)的总能量等于其傅里叶变换幅度平方下的面积。|F(f)|^2通常被称为能量密度energy density、谱密度spectral density或功率谱密度power spectral density函数，|F(f)|^2 df描述从f到f+dF的差分频带中包含的信号能量密度。

在许多电气工程应用中，需要瞬时信号功率，通常假设它等于信号幅度的平方，即f^2*(t)。

为了方便起见，假设系统中的信号通过一个1欧姆的电阻。例如，如果f(t)是施加在系统电阻R上的电压(电流)信号，则其真实瞬时功率表示为[f(t)^2]/R(或对于电流[f(t)^2]R)。因此，只有当R为1欧姆时，f^2*(t)才是真实功率。

对于周期信号来说，可以来定义在时间区域t1-t2上的平均功率Pavg，通过对[f(t)]^2从t1到t2积分，然后除以t2-t1得到平均值：

$P_{avg} = \frac{1}{t_{2}-t_{1}}\int_{t_{1}}^{t_{2}}{f^{2}}(t)dt=\frac{1}{T}\int_{0}^{T}{f^{2}}(t)dt$

其中T是信号的周期。

能量可以用功率P(t)的方式来表示：

$w(t) = \int_{-\infty }^{\infty }[{f}(t)]^{2}dt=\int_{-\infty }^{\infty }P(t)dt$

功率是能量的时间变化率：

$P(t)=\frac{dw(t)}{dt}$

|F(f)|^2和P(t)通常被称为能量密度、谱密度或功率谱密度函数PSD。此外，PSD可以被解释为与以fHz为中心的1Hz带宽相关的平均功率。

3、随机信号

使用傅里叶变换分析线性系统是广泛的，能够方便的处理周期信号。但是对于随机信号说，是否能够直接像周期信号一样直接进行傅里叶变换呢。经过一些修改，仍然可以。并且修改后的方法在处理随机信号和处理非随机信号方面提供了本质上相同的优势。

*随机信号(平稳/非平稳)：具有不确定性，幅度不能预知，非周期，但往往服从一定的统计特性。

二、经典功率谱估计方法

经典功率谱估计采用的传统傅里叶分析方法，主要分为自相关法(间接法)和周期图法(直接法)两种。

如何评价功率谱估计的好坏？——分辨率和方差

*分辨率：功率谱上能够区分的最小相邻频率成分，分辨率越高，我们观察信号的频率成分越清晰；

*方差：方差大小则反映到功率谱波动性的大小，如果方差太大，功率谱波动性大，则很容易造成有用的频率成分被噪声淹没。所以我们希望得到的功率谱，分辨率越高越好，方差越小越好。

1. 自相关法

1949年，Turkey根据Wiener-Khintchine定理提出对有限长数据进行谱估计的自相关法，即利用有限长数据估计自相关函数，再对该自相关函数求傅里叶变换，从而得到谱的估计。

1958年，Blackman和Tukey在出版的有关经典谱估计的专注中讨论了自相关谱估计法，所以自相关法又叫BT法。步骤如下：

(1) 由信号的有限个观察值x(0),x(1),...x(n-1)估计出自相关函数R(m)；

(2) 对R(m)做Fourier变换，得到功率谱；

*Wiener-Khintchine定理指出，随机信号的相关函数与它的功率谱是一对傅里叶变换对。

数据点数N分别为256、512和1024的BT法，得到的功率谱如图，方差的数值如表所示。

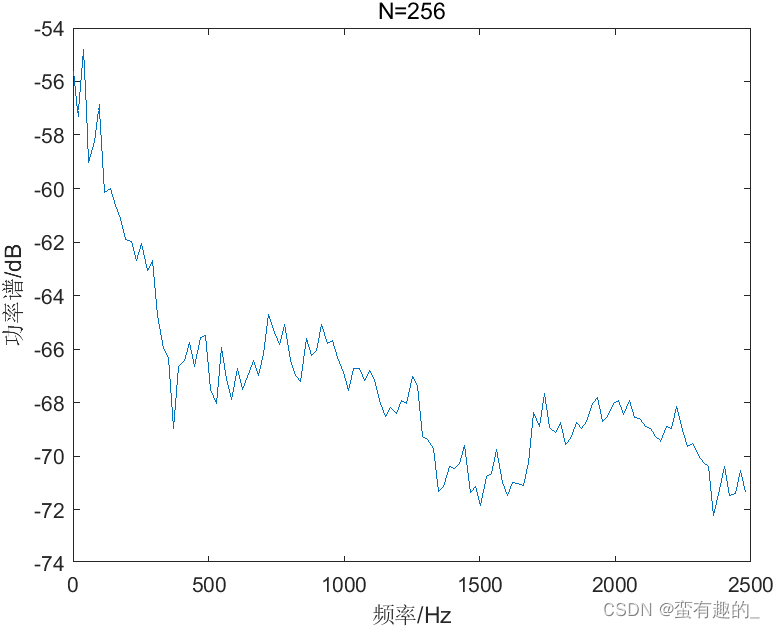
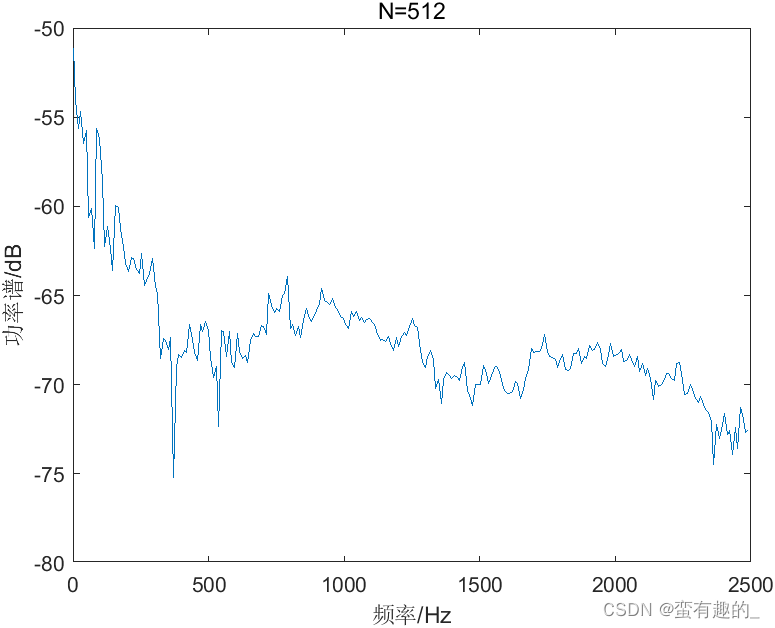
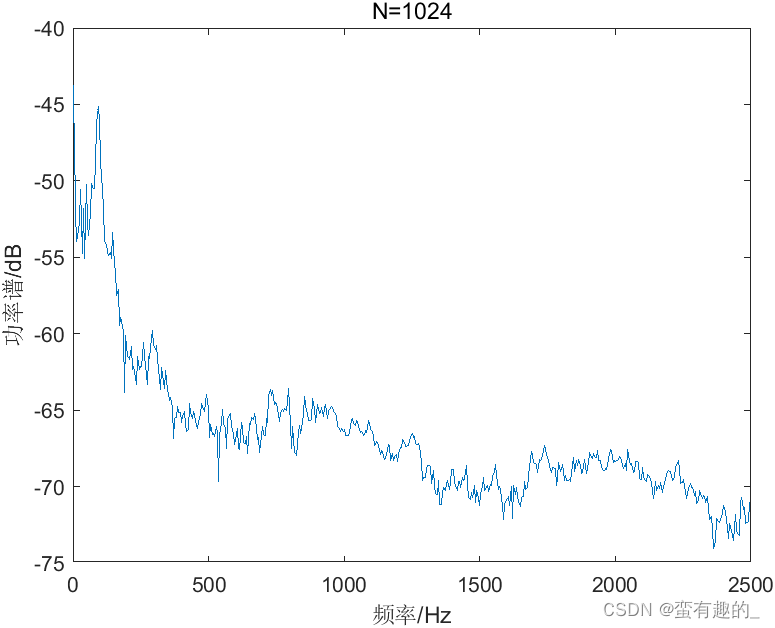
N	256	512	1024
方差	11.83	12.00	23.72

由结果发现，随N增大时，分辨率提高，方差变大。BT法没有解决分辨率与方差之间的矛盾。代码如下(N=1024)：

filename = 'sample.wav';%读取音频文件
[xn, Fs] = audioread(filename);%得到采样频率Fs和音频数据s 
nfft=1024;
cxn=xcorr(xn,'unbiased'); %计算序列的自相关函数
CX_fft=fft(cxn,nfft);
Pxx=abs(CX_fft);
index=0:round(nfft/2-1);
f=index*Fs/nfft;%计算频率范围
plot_Pxx=10*log10(Pxx(index+1));
plot(f,plot_Pxx);
xlabel('频率/Hz');
ylabel('功率谱/dB');
title('N=1024');
A = std(plot_Pxx)^2;

2、周期图法

1899年，Schuster首先提出周期图法(periodogram)，也称直接法。取平稳随机信号X(n)的有限个观察值x(0),x(1),...x(N-1)对功率谱S(w)进行估计。步骤如下：

(1) 从随机信号X(n)中截取N长的一段，把它视为能量有限信号；

(2) 对序列做傅里叶变换得到频谱；

(3) 取其幅度值的平方，并除以N。

*这是经典谱估计的最早提法，这种方法至今仍然被沿用，只不过现在是用快速傅里叶变换(FFT)来计算离散傅里叶变换(DFT)，用DFT的幅度平方作为信号中功率的度量。

当数据点数N分别为1280、2560和5120时，得到的功率谱分别如图所示，分辨率能够直观的通过功率谱图看出，方差的数值如表所示。

不同N值得到的功率谱的方差值
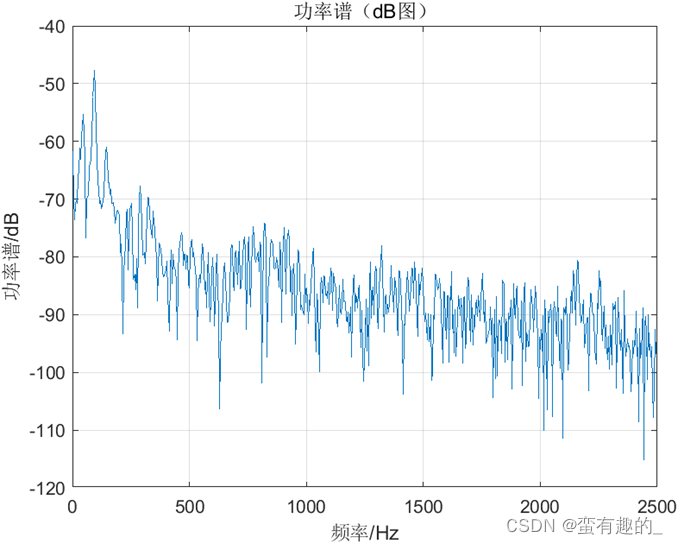
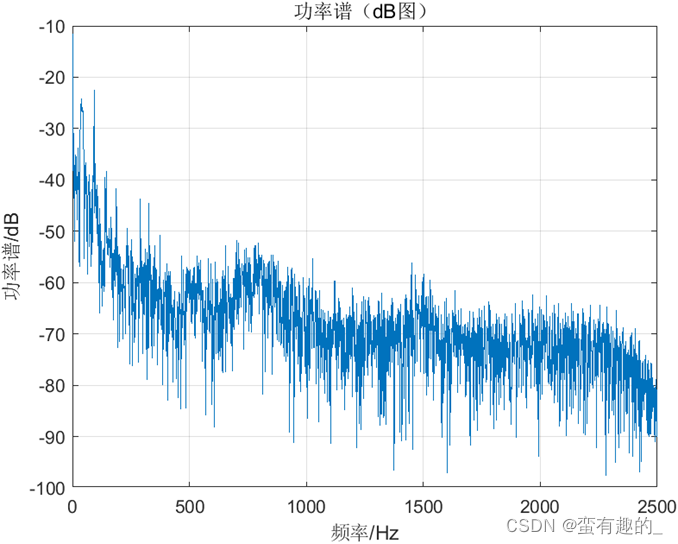
N	1280	2560	5120
方差	7.23e-13	2.48e-10	1.33e-6

通过上述结果，周期图法得到的功率谱随着数据点数N的增大，分辨率变大，方差也变大。代码如下：

filename = 'sample.wav';%读取音频文件
[xn, Fs] = audioread(filename);%得到采样频率Fs和音频数据s 
N=1280;%数据点选取
Nfft=N;
n=0:N-1;&数据点序列
xn = xn(1:N);%截取信号
P=10*log10(abs(fft(xn,Nfft).^2)/N);%傅里叶变换振幅谱平方的平均值，并转化为dB
f=(0:length(P)-1)*Fs/length(P);%频率序列
figure;
plot(f(1:N/2),P(1:N/2));
grid on;
title('功率谱（dB图）');
ylabel('功率谱/dB');
xlabel('频率/Hz');

3. 常见的改进周期图法

平均周期图法

周期图法得到的功率谱随着数据点数N的增大，分辨率变大、方差也变大。与我们所期望的“分辨率大，方差小”相矛盾。

为了改善这种性能。M.S.Bartlett提出了平均周期图法，即将信号序列x(n)分成互不重叠的若干段。对每个小段信号序列进行功率谱估计，然后再取平均作为整个序列x(n)的功率谱估计。步骤如下：

(1) 将信号x(n)分成互不重叠的段(段数为L)；

(2) 对每个小段信号序列进行功率谱估计；

(3) 取平均作为整个序列x(n)的功率谱估计。

当数据点数N为1280时，分段数分别为8，4，2时，平均功率谱的得到的功率谱分别如图所示。

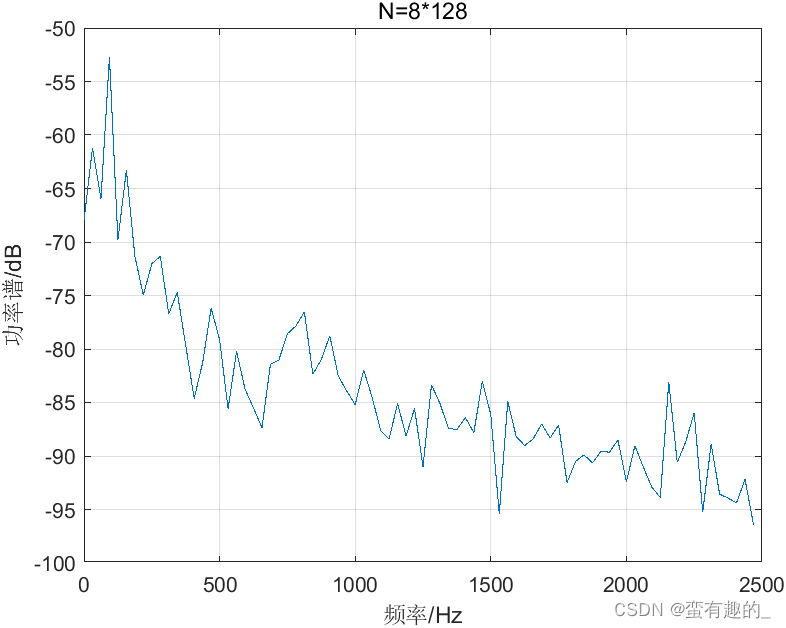
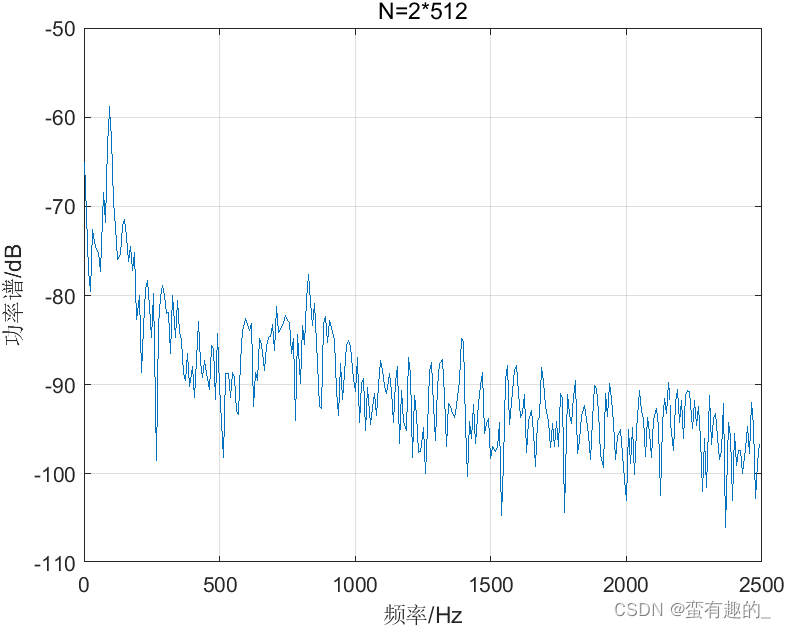
L	8	4	2
方差	3.67e-13	5.42e-15	7.45e-15

可以通过选择数据点数和分段数L，确定合适的分辨率和方差。

代码如下：

filename = 'sample.wav';%读取音频文件
[xn, Fs] = audioread(filename);%得到采样频率Fs和音频数据s 
Nsec=640;%FFT所用的数据长度
Pxx1=abs(fft(xn(1:640),Nsec).^2)/Nsec; %第一段功率谱
Pxx2=abs(fft(xn(641:1280),Nsec).^2)/Nsec;%第二段功率谱
Pxx=10*log10((Pxx1+Pxx2)/2);%Fourier振幅谱平方的平均值，并转化为dB
a11=std((Pxx1+Pxx2)/2)^2;
f=(0:length(Pxx)-1)*Fs/length(Pxx);%给出频率序列
figure;
plot(f(1:Nsec/2),Pxx(1:Nsec/2));%绘制功率谱曲线
xlabel('频率/Hz');
ylabel('功率谱/dB');
title('N=2*512');
grid on;
Nsec=320;%数据的长度和FFT所用的数据长度
Pxx1=abs(fft(xn(1:320),Nsec).^2)/Nsec; %第一段功率谱
Pxx2=abs(fft(xn(321:640),Nsec).^2)/Nsec;%第二段功率谱
Pxx3=abs(fft(xn(641:960),Nsec).^2)/Nsec;%第三段功率谱
Pxx4=abs(fft(xn(961:1280),Nsec).^2)/Nsec;%第四段功率谱
Pxx=10*log10((Pxx1+Pxx2+Pxx3+Pxx4)/4);%Fourier振幅谱平方的平均值，并转化为dB
a12=std((Pxx1+Pxx2+Pxx3+Pxx4)/4)^2;
f=(0:length(Pxx)-1)*Fs/length(Pxx);%给出频率序列
figure;
plot(f(1:Nsec/2),Pxx(1:Nsec/2));%绘制功率谱曲线
xlabel('频率/Hz');
ylabel('功率谱/dB');
title('N=4*256');
grid on;

Nsec=160;%数据的长度和FFT所用的数据长度
Pxx1=abs(fft(xn(1:160),Nsec).^2)/Nsec; %第一段功率谱
Pxx2=abs(fft(xn(161:320),Nsec).^2)/Nsec;%第二段功率谱
Pxx3=abs(fft(xn(321:480),Nsec).^2)/Nsec;%第三段功率谱
Pxx4=abs(fft(xn(481:640),Nsec).^2)/Nsec;%第四段功率谱
Pxx5=abs(fft(xn(641:800),Nsec).^2)/Nsec; %第五段功率谱
Pxx6=abs(fft(xn(801:960),Nsec).^2)/Nsec;%第六段功率谱
Pxx7=abs(fft(xn(961:1120),Nsec).^2)/Nsec;%第七段功率谱
Pxx8=abs(fft(xn(1121:1280),Nsec).^2)/Nsec;%第八段功率谱
Pxx=10*log10((Pxx1+Pxx2+Pxx3+Pxx4+Pxx5+Pxx6+Pxx7+Pxx8)/8);%Fourier振幅谱平方的平均值，并转化为dB
a13=std((Pxx1+Pxx2+Pxx3+Pxx4+Pxx5+Pxx6+Pxx7+Pxx8)/8)^2;

f=(0:length(Pxx)-1)*Fs/length(Pxx);%给出频率序列
figure;
plot(f(1:Nsec/2),Pxx(1:Nsec/2));%绘制功率谱曲线
xlabel('频率/Hz');
ylabel('功率谱/dB');
title('N=8*128');
grid on;

当观测样本序列数据个数N固定时，要降低方差需要增加分段数L。当N不大时分段长度M取值较小，则功率谱分辨率降低到较低水平。若分段数L固定时，增加分辨率需要分段长度M，则需要采集到更长的检测数据序列，实际中恰恰是检测样本序列长度不足。

修正的平均周期图法

上述方法提到的实际中检测样本序列长度是有限的，对现有数据长度N，如果能获得更多的段数分割，将会得到更小的方差。允许数据段间有重叠部分，来得到更多的段数，对段间重叠长度的选取，最简单的是取段长度M的一半。

P. D. Welch在Bartlett方法的基础上进一步改进，提出一种将加窗处理与分段平均相结合的方法，其采用信号重叠分段、加窗、FFT等技术来计算功率谱。

数据截取的过程中相当于数据加矩形窗，矩形窗幅度较大的旁瓣会造成“频谱泄漏”。在分段时采取的窗函数更为多样(三角窗，海明窗等)，以减小截断数据(加矩形窗)窗函数带来的影响。

步骤如下：

(1) 先对信号x(n)进行重叠分段，如按2：1重叠分段，即前一段信号和后一段信号有1/2重叠；

(2) 然后用非矩形窗口对每一小段信号序列进行预处理，再采用前述分段平均周期图法进行整个信号序列x(n)的功率谱估计。

*与周期图法比较，Welch法可较大改善谱曲线的光滑性，并提高谱估计的分辨能力。

当选择不同窗函数(矩形窗、汉明窗、blackman窗)，利用pwelch函数进行谱估计。结果如图所示：

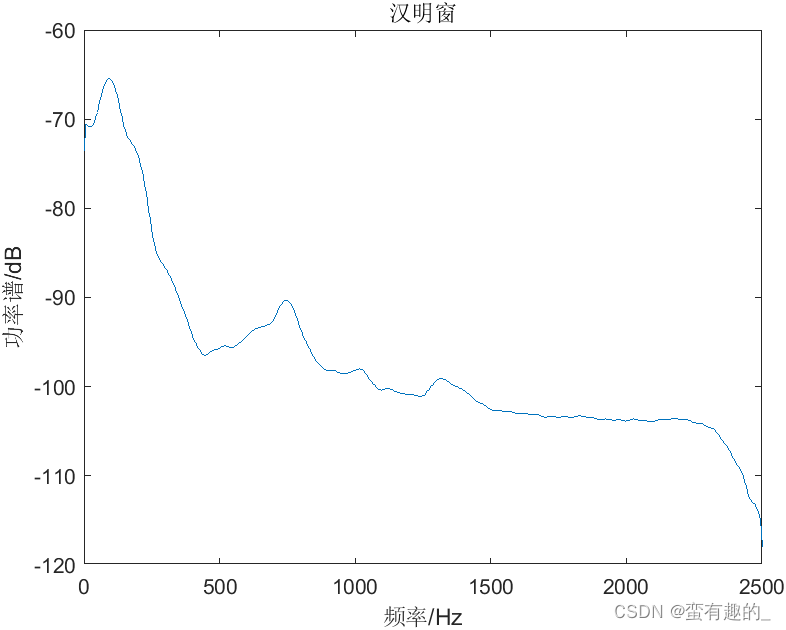
代码如下：

filename = 'sample.wav';%读取音频文件
[xn, Fs] = audioread(filename);%得到采样频率Fs和音频数据s 
nfft=xn;
window=boxcar(100); %矩形窗
window1=hamming(100); %海明窗
window2=blackman(100); %blackman窗
noverlap=50; %重叠
range='onesided'; %频率间隔为[0 Fs/2]，只计算一半的频率
[Pxx,f]=pwelch(xn,window,noverlap,nfft,Fs,range);
[Pxx1,f1]=pwelch(xn,window1,noverlap,nfft,Fs,range);
[Pxx2,f2]=pwelch(xn,window2,noverlap,nfft,Fs,range);
plot_Pxx=10*log10(Pxx);
plot_Pxx1=10*log10(Pxx1);
plot_Pxx2=10*log10(Pxx2);

figure
plot(f,plot_Pxx);title('矩形窗');

figure
plot(f1,plot_Pxx1);title('汉明窗');

figure
plot(f2,plot_Pxx2);title('blackman窗');

参考资料：互联网内容