随机信号功率谱估计方法matlab仿真

1. 引言

信号的频谱分析是研究信号特性的重要手段之一, 对于确定性信号, 可以用 Fourier 变换来考察其频谱性质, 而对于广义平稳随机信号, 由于它一般既不是周期的, 又不满足平方可积, 严格来说不能进行 Fourier 变换, 通常是求其功率谱来进行频谱分析 。然而, 实际应用中的平稳随机信号通常是有限长的,只能根据有限长信号估计原信号的真实功率谱, 这就是功率谱估计问题。功率谱估计分为经典谱估计和现代谱估计, 本文分别研究了经典估计法和现代估计法中的相关图法、周期图法和自相关法、burg法。

1. 算法原理
   1. 背景

功率谱反映了随机信号各频率成份功率能量的分布情况, 可以揭示信号中隐含的周期性及靠得很近的谱峰等有用信息, 应用极其广泛, 例如, 在语音信号识别 、雷达杂波分析 、地震勘探信号处理 、水声信号处理 、系统辨识中非线性系统识别 、物理光学中透镜干涉 、流体力学的内波分析 、太阳黑子活动周期研究等许多领域, 发挥了重要作用 。

1. 1. 经典谱估计算法

经典谱估计又称非参数模型谱估计, 主要方法有 : 相关图法，周期图法及改进的周期图估计法 。本文主要研究对比相关图法的矩形窗、三角窗法和周期图法的Bartlett估计、Welch估计。

2.2.1相关图法

相关图法是1958年由Blackman与Tukey首先提出的,理论基础是维纳辛钦定理,基本思想是通过改善对相关函数的估计方法,对周期图进行平滑处理以改善周期图谱估计的方差性能,亦称BT法、间接法 。

相关图法的算法流程图如下：

图1 相关图法流程图

具体步骤如下：

第一步：从无限长随机序列X(n)中截取长度N的有限长序列XN(n)。

第二步：由N长序列XN(n)求（2M-1）点的自相关函数序列RX(m)。即

RXm=1Nn=0N-1XNnXNn+m#1

这里，m=-(M-1),…,-1,0,1,…,M-1，MN，RX(m)是双边序列，但是由自相关函数的偶对称性式，只要求出m=0,。。。,M-1的RX(m)，另一半也就知道了。

第三步：由相关函数的傅式变换求功率谱。即

SXejω=m=-M-1M-1RXme-jωm#2

2.2.2周期图法

Schuster 于1899年首先提出周期图法,也称直接法,取平稳随机信号 X(n)的有限个观察值x(0),x(1),…,x(N-1)对功率谱S(ω)进行估计。

周期图法的算法流程图如下：

图2 周期图法流程图

具体步骤如下：

1.从随机信号x(n)中截取N长的一段，把它视为能量有限信号，直接取

XN（n)的傅式变换，得频谱XN（k)，

XNejω=n=0N-1xnne-jωn#3

2.取其幅值的平方，并除以N，作为对x(n)真实功率谱Sx（ejω)的估计

Sx（ejω)的估计，即

Sxejω=1NXNejω2#4

2.2.3改进的经典谱估计方法

相关法和周期图法都是用随机选取的N个数据对随机过程进行功率谱估计，它隐含着对无限长数据加了一个矩形窗截断。时域中与矩形窗函数相乘对应于频域中与矩形窗频谱相卷积，由于矩形窗频谱不同于冲击函数，所以所得结果的谱估计不同于真实的功率谱。为了使估计逼近真实谱，应设法使窗函数谱幅度函数逼近冲击函数。矩形窗频谱与冲击函数相比存在两方面差异，一是主瓣不是无限窄，二是有旁瓣。由于主瓣不是无限窄，使得功率向附近扩散，使信号模糊，降低了分辨率，主瓣越宽分辨率越低。由于旁瓣的存在又会产生两个结果，一是功率谱主瓣内的能量泄露到旁瓣使谱估计方差增大，二是与旁瓣卷积后得的功率谱完全属于干扰。严重情况下会使弱信号淹没在强信号的干扰中，无法检测出来，这是经典谱估计的主要缺点。

为了减少这些缺点造成的影响，对古典谱估计做了改进，现在比较常用的改进方法是Bartlett法和Welch法。下面分别作介绍。

Bartlett法

为改善周期图较差的方差性能，M. S. Bartlett 提出平均周期图法，即将信号序列x(n)分成互不重叠的若干段，对每个小段信号序列进行功率谱估计，然后再取平均作为整个序列 x(n) 的功率谱估计。

图3 Bartlett法流程图

Welch法

P. D. Welch 在此基础上作出进一步改进，提出一种将加窗处理与分段平均相结合的方法。其采用信号重叠分段、加窗、FFT等技术来计算功率谱。先对信号 x(n) 进行重叠分段，如按 2∶ 1 重叠分段，即前一 段信号和后一段信号有 1 /2 是重叠的，然后用非矩形窗口对每一小段信号序列进行预处理，再采用前述分段平均周期图法进行整个信号序列x(n)的功率谱估计。与周期图法比较，Welch法可较大改善谱曲线的光滑性，并提高谱估计的分辨能力。

图4 Welch法示意图

其主要步骤是：

1.将N长的数据段分成L个小段，每小段M点，相邻小段间交叠M/2点（即2:1分段）。因为L（M/2）+M/2=N,所以段数

L=N-M2M2#5

2.对各小段加同样的平滑窗ω(n)后起傅氏变换

Xiejω=n=0M-1xinωne-jωn,i=1,…,L, #6

3.用下式求各小段功率谱的平均

这里， U=1Mn=0M-1ω2(n)代表窗函数平均功率，MU是M长窗函数的能量。

Welch法得出的Sx(ejω)是无偏谱估计，当段数 L增大时方差减小，Sx(ejω)趋于一致估计，分段平均减小了由数据样本本身的随机性带来的方差，段数越多方差越小，但分辨率下降。分段多了每段的点数必然少了，所以采用2:1分段，拉长了每小段长度，有利于平滑过渡。

2.3 现代谱估计算法

现代谱估计是针对经典谱估计方差性能较差、分辨率较低的缺点提出并逐渐发展起来的，其又分为参数模型谱估计和非参数模型谱估计。参数模型谱估计主要有 AＲ 模型、MA 模型、AＲMA 模型、Prony 模型等，其中AR模型应用最多。非参数模型谱估计主要有 MTM 法、MUSIC 法、特征向量法、最小方差法等。本文主要研究参数模型估计中的AR模型，并终点研究了自相关法和Burg法。

2.3.1自相关法

ARMA模型功率谱的数学表达式为

Pejω=σ21+k=1qbke-jωk21+k=1pake-jωk2#7

其中，Pejω 为功率谱密度; s2是激励白噪声的方差; ak 和bk 为模型参数。

若ARMA 模型中 bk 全为 0，则变成了AR模型，又称线性自回归模型，其是一个全极点模型

Pejω=σ21+k=1pake-jωk2#8

而若 AＲMA 模型中ak全为0,则变成了MA模型，是一个全零点模型

Pejω=σ21+k=1qbke-jωk2#9

研究表明，AＲMA 模型和 MA 模型均可用无限阶 的 AＲ 模 型 来 表 示。且 AＲ 模型的参数估计计算 相对简 单。同 时，实际的物理系统通常是全极点系统。

其中，Ｒ( m) = E［x( n) x( n + m) ］为信号序列 x( n) 的 自相关函数。 目前求解 Yule － Walker 方程主要有3 种: Levinson － Durbin 递推算法、Burg 算法和协方差方法。

自相关法的步骤如下：

第一步 :估计观测序列的自相关系数矩阵 ;

第二步:利用Lenvinson-Durbin 递推算法求 解 AR模型参数。

Lenvinson -Durbin算法是从低阶开始递推,直 到 p阶,给出了每一阶次的所有参数, 这有利于选择 合适阶次的 AR模型。由于自相关法等效于对前向 序列误差epf(n)前后加窗,加窗的结果使得自相关法的频率分别率降低。数据越短,分别率越低。

2.3.2 Burg法

Burg算法与自相关法不同, 它是使序列 x(n) 的前后向预测误差功率之和:

ρpfb=1N-Pn=pN-1{ epfn2+epbn2}最小。

利用 Burg法求解 AR模型参数的步骤:

图5 Burg法流程图

第一步:由初始条件ef0(n)=x(n)和eb0(n)=x(n),根据式,,求出反射系数k1 ;

第二步:根据序列x ( n)的自相关函数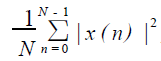,求出阶次m = 1时的AR模型参数a11=k1 与前后向预测误差功率之和ρ1fb=(1-k12)rx(0);

第三步:由式求出前向预测误差e1f( n)与后向预测误差e1b(n) ( n) , 然后由式估计出反射系数k2 ;

#11

第四步:由式(10) Levinsion递推关系,求出阶次m =2时的AR模型参数a2(1)和a2(2) ,以及ρ2fb ;

#12

第五步:重复上述过程, 直到阶次m = p, 这样就求出了所有阶次的AR模型参数。

1. 实验结果与分析
   1. 相关图法
      1. matlab信号预处理

本文选取鸟叫声为处理样本，作为本文的随机信号，首先对信号做预处理，结果如下图所示：

图6 预处理前后时域波形

利用matlab的频谱分析得到，便于与以后做对比分析：

图7 鸟叫理论功率

1. 1. 1. 相关图法矩形窗

利用相关图法加矩形窗对鸟叫信号做处理得：

图8 矩形相关图与理论做对比

1. 1. 1. 相关图法三角窗

利用相关图法加三角窗对鸟叫信号做处理得：

图9 三角窗相关图与理论对比

由上述仿真图可见，三角窗较矩形窗估计毛刺减小，功率谱变得更为平滑。M随着N的增大而增大时，分辨率提高，方差变大。相关图法存在分辨率与方差之间的矛盾，但是相关图法得到的功率谱当N为无穷大时，方差会趋向于零，即为一致估计。

1. 1. 周期图法
      1. Bartlett谱估计

        Bartlett方法就是把数据分D段，每段fft模平方除以每段长度，再把D段的s相加再平均：

图10 Bartlett估计与理论对比

1. 1. 1. Welch谱估计

Welch方法就是有重复的分段：

图11 Welch谱估计与理论对比

1. 1. 1. 经典功率谱估计对比

图12 经典谱改进估计对比

   

由上述仿真实验可知，Bartlett估计与Welch估计对周期图法做了改进，得到的功率谱更加平滑，便于问题的分析。无论是周期图法及其改进算法都没有从根本上解决分辨率与方差的矛盾。经典功率谱估计是利用傅里叶变换估计功率谱，而我们之前分析随机信号不满足傅里叶变换的条件，所以经典功率谱估计方法不得不从无限长数据点截取有限长数据点，加入限制条件（周期图法实际上假定N点外数据周期重复、BT法假定N点外数据为零）来"强制"作傅里叶变换，这也是造成它局限性的原因。

1. 1. 自相关法

图13 自相关法与理论对比

1. 1. Burg谱估计法

图14 Burg法与理论对比

1. 结论

通过上述实验可以直接看出以下特性

1. 经典功率谱估计的方差大，谱分辨率差。采用经典的傅里叶变换及窗口截断，对长序列有良好估计。
2. 现代谱的分辨率较高。这是由于在时域的开窗，使得在频域发生“频谱泄露”，即功率谱的主瓣能量泄漏到旁瓣中，导致弱信号的主瓣被强信号的旁瓣所湮没，造成谱的模糊。
3. 周期图法收敛性较好，曲线平滑，但是功率谱主瓣较宽，分辨率低，这是由于对随机序列的分段处理引起了长度有限所带来的Gibbs现象而造成的。

MATLAB code:
代码1
close all;clear all;
% read speech waveform from a file
[s, fs] = audioread('鸟叫.wav');
% set analysis parameters, pre-emphasise and windowing
N = 8192;
Nfft = 8192;
n0 = 1000;
x = s(n0 : n0+N-1);
x=x';
x1 = filter([1 -0.97], 1, x); %预加重 滤波器
w = (window('hamming', N));
xw = x1.*w;
Sxw = fft(xw, Nfft);
Sxdb = 20*log10(abs(Sxw(1 : Nfft/2))) - 10*log10(N);
figure;
subplot(2,1,1);
plot(s);  xlim([0 length(s)]); ylim([-0.2 0.2]);
ylabel('幅度');  xlabel('时间');
title('预处理前时域波形');
subplot(2,1,2);
plot(xw); xlim([0 length(x)]); ylim([-0.1 0.1]);
ylabel('幅度');  xlabel('时间'); 
title('预处理后时域波形');
%%
f = (0 : Nfft/2-1)*fs / Nfft / 1000;%取前一半 后一半是翻转
plot(f, Sxdb);
ylabel('强度 (dB)');  xlabel('频率(kHz)');
title('鸟叫理论功率谱');
%%
r = zeros(2*N/2-1, 1); 
for k = 1 : N/2
    x1 = x(k : N);
    x2 = x(1 : N+1-k);
    r(N/2+k-1) = x1'* x2 / N;
    r(N/2-k+1) = r(N/2+k-1);    %r(-k) = r(k)
end
f = (0 : Nfft/2-1)*fs / Nfft / 1000; 
rx = r ;
Sxz1 = fft(rx, Nfft);
Sxdbz1 = 10*log10(abs(Sxz1(1 : Nfft/2)));
subplot(4,1,1);
plot(f, Sxdbz1);
ylabel('强度 (dB)');  xlabel('频率 (kHz)');
title('相关图 (矩形窗)');
%----------------相关图法 三角窗 --------------%
w = triang(2*N/2-1)'; %三角窗 加窗后效果
rx = r .* w';
Sxz2 = fft(rx, Nfft);
Sxdbz2 = 10*log10(abs(Sxz2(1 : Nfft/2)));
subplot(4,1,2);
plot(f, Sxdbz2);
ylabel('强度 (dB)');  xlabel('频率 (kHz)');
title('相关图 (三角窗)');
%%
Sx = zeros(1, Nfft/2);K = 4; L = N/K;
for k = 1 : K
    ks = (k-1)*L + 1;
    ke = ks + L - 1;
    X = fft(x(ks:ke), Nfft);
    X = (abs(X)).^2;        
    for i = 1 : Nfft/2
        Sx(i) = Sx(i) +X(i);
    end
end

for i = 1 : Nfft/2
    Sx(i) = 10*log10(Sx(i)/(K*L));
end
subplot(4,1,3);
plot(f, Sx);
ylabel('强度 (dB)');  xlabel('频率 (kHz)');
title('Bartlett 估计, N=4096, K=4, D=L=1024')
%%
%----------------周期图法 Welch谱估计--------------%
Nfft = 8192; 
K = 4; 
D = fix(Nfft/2 / (K+1));%向0方向靠拢取整 分为K+1格，可以重叠K次做fft
L = 2*D;
Sxw = zeros(1, Nfft/2);
w = (window('hamming', L))';
for k = 1 : K
    ks = (k-1)*D + 1;
    ke = ks + L - 1;
    xk = x(ks:ke)' .* w; %时域加窗
    X = fft(xk, Nfft);
    X = (abs(X)).^2;
    for i = 1 : Nfft/2
        Sxw(i) = Sxw(i) + X(i); 
    end
end
for i = 1 : Nfft/2
    Sxw(i) = 10*log10(Sxw(i)/(K*L)); 
end
subplot(4,1,4);
plot(f, Sxw);
ylabel('强度 (dB)'); xlabel('频率 (kHz)');
title('Welch 估计, N=4096, K=4, D=819, L=1638');
代码2
close all;clear all;
% read speech waveform from a file
[y, fs] = audioread('鸟叫.wav');
N = 8192;
Nfft = 8192;
n0 = 1000;
x = y(n0 : n0+N-1);
x=x';
x1 = filter([1 -0.97], 1, x); 
w = (window('hamming', N));
xw = x1.*w;
% Estimate PSD of the short-time segment
Sxw = fft(xw, Nfft);
Sxdb = 20*log10(abs(Sxw(1 : Nfft/2))) - 10*log10(N);
figure;
subplot(2,1,1);
plot(y);  xlim([0 length(y)]); ylim([-0.2 0.2]);
ylabel('幅度');  xlabel('时间');
title('预处理前时域波形');
subplot(2,1,2);
plot(xw); xlim([0 length(x)]); ylim([-0.1 0.1]);
ylabel('幅度');  xlabel('时间'); 
title('预处理后时域波形');
%%
%-----------自相关（yule-walker,levinson）算法-----------%
p=20;                    
a=zeros(p,p);
s=zeros(1,p+1);
for m=1:N
    r=0;
    for n=1:(N-m)
        r=r+y(n)*y(n+m-1);
    end
    rx(m)=r/N;
end
a(1,1)=-rx(2)/rx(1);
q(1)=rx(1)*(1-a(1,1)^2);
for m=2:p;
    s=0;
for j=1:m-1;
s=s+a(m-1,j)*rx(m-j+1);
end
k(m)=-(rx(m+1)+s)/q(m-1);
a(m,m)=k(m);
for i=1:m-1;
a(m,i)=a(m-1,i)+k(m)*a(m-1,m-i);
q(m)=q(m-1)*(1-k(m)^2);
end
end
s=[1,a(p,:)];
P=abs(fft(s,1000)).^2;
Pw=10*log(q(p)./P);
w=(0:N-1)/N;
f=0:0.001:0.999;
M=length(f);
subplot(2,1,1);
f = (0 : Nfft/2-1)*fs / Nfft / 1000; 
plot(f, Sxdb);
ylabel('强度 (dB)');  xlabel('频率(kHz)');
title('鸟叫理论功率谱');
subplot(2,1,2);
% plot(f(1:M/2),Pw(1,1:M/2));
plot(f,Pw);
ylabel('10log(PSD)');
title('自相关算法功率谱');
%%
sigLength=162500;     
Nfft=8192;          
fs=10000;           
p=6;                
n=0:sigLength-1;
t=n/fs;          
subplot(2,1,1);a
f = (0 : Nfft/2-1)*fs / Nfft / 1000; 
plot(f, Sxdb);
ylabel('强度 (dB)');  xlabel('频率(kHz)');
title('鸟叫理论功率谱');
[Pxx1,f]=pmem(y(:,1),p,Nfft,fs);  
subplot(2,1,2);
plot(f,10*log10(Pxx1));               
xlabel('频率/Hz');ylabel('功率谱/dB');
title('Burg谱估计');
grid on

参考文献：

[1] 俱莹, 何佳, 胡稷鑫. 经典功率谱估计方法的研究[J]. 数字通信世界, 2015, (4):47-50.

[2] Wang Guolin，Liu Yongchen. The methods of power spectrum estimation based on measured pavement［C］. International Conference on Electric Information and Control Engineering，2011，P2787-2790

[3] Yao Yu，Heming Zhao. A new method for noise power spectrum estimation［C］. 4th IET International Conference on Wireless，Mobile & Multimedia Networks，2011，P206-209

[4] John G. Proakis，Dimitris G. Manolakis. Digital Signal Processing-Principles，Algorithms，and Applications（Fourth Edition）［M］. Prentice Hall，2007

[5]王立琦，王铭义，张礼勇，江连洲，于殿宇.谱估计中解析公式与卡尔曼滤波比较研究［J］.哈尔滨工程大学学报，2010，31（1）: 115-119