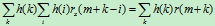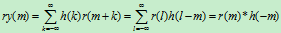经典谱估计方差性能差,分辨率较低。
方差性能差:无法实现功率谱密度的求均值和求极限
分辨率低:周期图发是假设数据窗之外的均是0,自相关法是延迟窗之外的均为0。
现代谱估计就是为了改善上述问题,参数模型法是现代谱估计的主要内容,思路如下:
- 假设所研究的过程x(n)是由一个输入序列u(n)经过一个LTI(linear time invairiable)线性系统H(Z)的输出,如下图1所示:
- 有x(n)或自相关函数r(m)来估计H(z)的参数
-
有H(z)来估计功率谱
图1
对于图1,由于系统是线性系统,有如下关系:
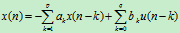
及
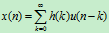
把(1)式的x项左移,对两边做Z变换,假设b0=1,有:

式中:
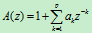


这里引入一个关系式并证明:
如果X(n)为平稳随机信号,经过线性系统H(z)的输出为Y(n),如下:
Y(n)=X(n)*h(n)(*为卷积符号),则有如下关系式
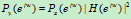
现证明5式:
=
=
式中:
令m+k=l,则有:
于是(5)式得以证明。
对(5)式做傅里叶变换,由于自相关函数和功率谱密度是一个傅里叶变换对,因此,(6)式也得以证明。
现在再回到正题。假设输入序列u是一个方差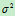
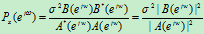
如果激励白噪声的方差和模型参数
现在分三种情况来讨论:
-
如果
都是0,那么(1)(3)(7) 就变成了如下表达式:
----------(8)
----------(9)
----------(10)
这种情况下称为自回归(auto-regressive)模型,简称AR模型,这是一个全极点模型(分子不可能为0,无零点,只有分母是由可能为0)。自回归的含义是系统的输出是当前的输入和过去p个输出的加权和。
-
如果
为0,那么(1)(3)(7) 就变成了如下表达式
(b0=1) ----------(11)
---------(12)
----------(13)
这种情况下称为移动平均(moving-average)模型,这是一个全零点模型。
- 如果
都不为0,称为ARMA模型,是一个既有零点又有极点的模型。

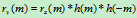 .
.