算术优化算法（Arithmetic Optimization Algorithm，AOA）

一、算法灵感
二、算法介绍
三、实验结果
四、参考文献

一、算法灵感

算术优化算法(Arithmetic Optimization Algorithm, AOA)是由学者 Laith Abualigah 等人于2021年提出的一种新型元启发式优化算法，其灵感来源于算术中的四则混合运算。算法通过数学函数加速器选择优化策略，将整个过程分为探索和开发，即利用乘除运算进行全局探索，利用加减运算进行局部开发。

二、算法介绍

2. 1 初始化

首先，AOA会生成一个均匀分布的随机种群。初始种群可由以下公式求得
$X\left( {i,j} \right) = Rand \times \left( {Ub - Lb} \right) + Lb \tag{1}$ 其中， $U b$ 为上界， $L b$ 为下界， $R an d$ 为 $[0, 1]$ 之间的随机数， $X (i ， j)$ 是第 $i$ 个解在第 $j$ 维空间的位置。

2. 2 数学函数加速器MOA

根据MOA的值判断进行全局探索还是局部开发：
$MOA\left( t \right) = Min + t \times { {\left( {Max - Min} \right)} \over T} \tag{2}$ 其中， $r_{1}$ 为 $[0, 1]$ 之间的随机数， $MO A (t)$ 为当前的加速函数值， $M in$ 为加速函数的最小值， $M a x$ 为加速函数最大值， $T$ 为最大迭代次数， $t$ 为当前迭代次数；当 $r_{1}<MOA(t)$ 时，函数将进入全局探索阶段，反之则进入局部开发阶段。

2. 3 探索阶段

根据随机数 $r_{2}$ 决定采用乘法或除法策略，两种策略离散度高，有利于粒子在算法空间内探索，计算公式如下：
${X_{\left( {t + 1} \right)}} = \left\{ { { \begin{aligned} & { {X_b}\left( t \right) \div \left( {MOP + \varepsilon } \right) \times \left( {\left( {Ub - Lb} \right) \times \mu + Lb} \right)\ \ ,} { {r_2} < 0.5,} \cr &{ {X_b}\left( t \right) \times MOP \times \left( {\left( {Ub - Lb} \right) \times \mu + Lb} \right)\quad\quad\quad,} {otherwise.} \cr \end{aligned} } } \right. \tag{3}$ 其中， $r_{2}$ 为 $[0, 1]$ 的随机数， $X (t + 1)$ 为下一代粒子的位置， $X_{b}(t)$ 为当前适应度最佳粒子的位置， $μ$ 为搜索过程控制系数(值为0.499)， $ε$ 为极小值， $MOP$ 为数学优化器概率，其计算公式如下：
$MOP\left( t \right) = 1 - {\left( { {t \over T}} \right)^{1 \over \alpha} } \tag{4}$ 式中， $MOP (t)$ 为当前数学优化器概率， $α$ 为迭代敏感系数， $α$ 值越高迭代次数对 $MOP (t)$ 影响越大。

2. 4 开发阶段

算术优化算法通过加法策略和减法策略进行局部开发，两种策略均具有显著的低分散性，可以容易地接近目标，有利于算法更快寻找最优解。其计算公式如下：
${X_{\left( {t + 1} \right)}} = \left\{ {\begin{aligned} { {X_b}\left( t \right) - MOP \times \left( {\left( {Ub - Lb} \right) \times \mu + Lb} \right),} & { {r_3} < 0.5,} \cr { {X_b}\left( t \right) + MOP \times \left( {\left( {Ub - Lb} \right) \times \mu + Lb} \right),} & {otherwise.} \cr \end{aligned} } \right. \tag{5}$ 其中， $r_{3}$ 为 $0$ 到 $1$ 之间的随机数。

2. 5 算法伪代码

初始化算术优化算法参数 $α$ ， $µ$
随机初始化解决方案的位置 $X_{i}(i=1, 2, ..., N)$
While $t < T$ do
计算每个解的适应度值
找到适应度值最小的解(最佳解)
利用公式(2)更新 $MO A$ 值
利用公式(4)更新 $MOP$ 值。
For $i = 1$ to $N$ do
For $j = 1$ to $D im$ do
生成 $[0 ， 1]$ 之间的随机值( $r_{1}$ ， $r_{2}$ 和 $r_{3}$ )
If $r_{1}>MOA$ then
If $r_{2}<0.5$ then
使用等式(3)中的第一条公式应用除法运算符更新第 $i$ 个解的位置
Else
使用等式(3)中的第二条公式应用乘法运算符更新第 $i$ 个解的位置
End If
Else
If $r_{3}<0.5$ then
使用等式(5)中的第一条公式应用减法运算符更新第 $i$ 个解的位置
Else
使用等式(5)中的第二条公式应用加法运算符更新第 $i$ 个解的位置
End If
End If
End For
End For
$t = t + 1$
End While
返回最优解

三、实验结果

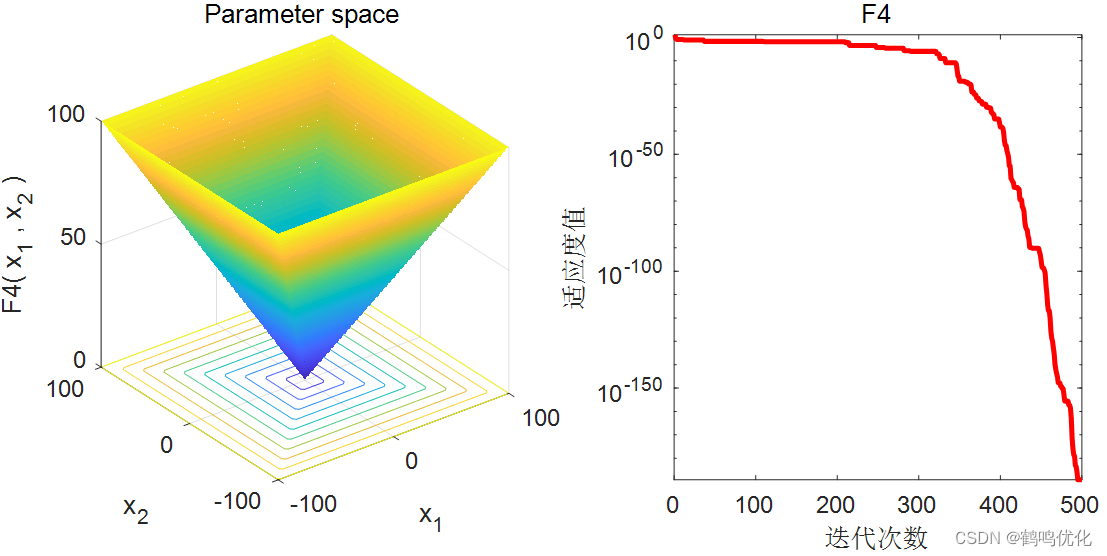
AOA在23个经典测试函数(设置维度 $d im = 30$ )的F4、F6、F8中的收敛曲线，测试函数公式如下：

函数	公式	理论值
F4	${F_4}(x) = \max \{ \left\| { {x_i}} \right\|,1 \le i \le d\}$	$0.00$
F6	${F_6}(x) = {\sum\nolimits_{i = 1}^n {({x_i} + 5)} ^2}$	$0.00$
F8	${F_8}(x) = \sum\nolimits_{i = 1}^d { - {x_i}\sin (\sqrt {\|{x_i}\|} )}$	$- 418.9829 \times d im$

3. 1 F4收敛曲线

$\end{aligned}$

3. 2 F6收敛曲线

在这里插入图片描述

3. 3 F8收敛曲线

在这里插入图片描述

四、参考文献

[1] Abualigah L, Diabat A, Mirjalili S, et al. The Arithmetic Optimization Algorithm[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 376, 113609.