目录
数据结构+算法(+设计模式)=程序
一、学习要点
理解算法的概念。
掌握算法的计算复杂性概念。
掌握算法复杂性的渐近性态的数学表述。
了解NP类问题的基本概念。
二、算法的定义
顾名思义,计算(求解)的方法
算法(Algorithm):对特定问题求解步骤的一种描述,是指令的有限序列。
算法是指解决问题的一种方法或一个过程。
程序设计=数据结构+算法(+设计模式)
三、算法的性质
算法是若干指令的有穷序列,满足性质:
(1)输入:有外部提供的量作为算法的输入。
(2)输出:算法产生至少一个量作为输出。
(3)确定性:组成算法的每条指令是清晰,无歧义的。
(4)有限性:算法中每条指令的执行次数是有限的,执行每条指令的时间也是有限的。
四、程序(Program)
程序是算法用某种程序设计语言的具体实现。
程序可以不满足算法的性质。
例如操作系统,是一个在无限循环中执行的程序,因而不是一个算法。
操作系统的各种任务可看成是单独的问题,每一个问题由操作系统中的一个子程序通过特定的算法来实现。该子程序得到输出结果后便终止。
五、问题求解(Problem Solving)
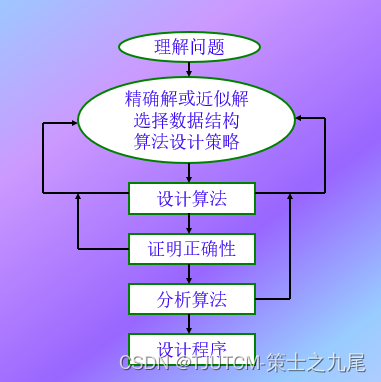
六、算法的描述
自然语言或表格
伪码方式
C++语言
Java语言
C语言
Python等其他语言
七、算法分析的目的
对算法所需要的两种计算机资源——时间和空间进行估算
设计算法——设计出复杂性尽可能低的算法
选择算法——在多种算法中选择其中复杂性最低者
八、算法复杂性分析
算法复杂性是算法运行所需要的计算机资源的量,
需要时间资源的量称为时间复杂性,需要的空间资源的量称为空间复杂性。
这个量应该只依赖于算法要解的问题的规模、算法的输入和算法本身的函数。
如果分别用N、I和A表示算法要解问题的规模、算法的输入和算法本身,而且用C表示复杂性,那么,应该有C=F(N,I,A)。
一般把时间复杂性和空间复杂性分开,并分别用T和S来表示,则有: T=T(N,I)和S=S(N,I)(通常,让A隐含在复杂性函数名当中)
(一)算法时间复杂性分析
最坏情况下的时间复杂性:
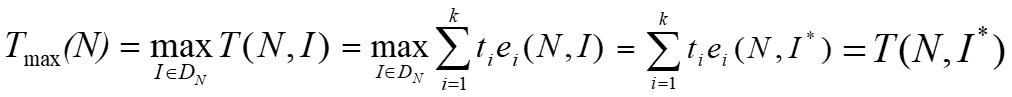
最好情况下的时间复杂性:
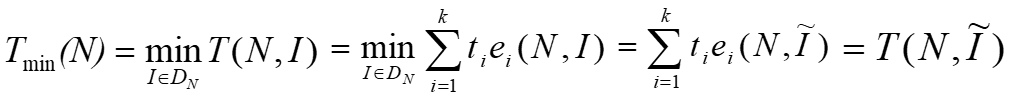
平均情况下的时间复杂性:
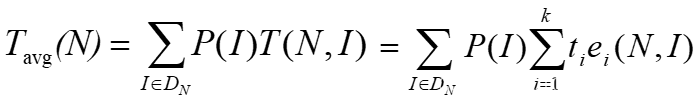
其中DN是规模为N的合法输入的集合;I* 是DN中使T(N, I*)达到Tmax(N)的合法输入; 是中使T(N, I*)达到Tmin(N)的合法输入;而P(I)是在算法的应用中出现输入I的概率。
(二)算法渐近复杂性
T(n) →∞ , 当 n→∞ ;
(T(n) - t(n) )/ T(n) →0 ,当 n→∞;
t(n)是T(n)的渐近性态,为算法的渐近复杂性。
在数学上, t(n)是T(n)的渐近表达式,是T(n)略去低阶项留下的主项。它比T(n) 简单。
1、渐进上界记号-大O符号
若存在两个正的常数c和n0,对于任意n≥n0,都有T(n)≤c×f(n),则称T(n)=O(f(n))
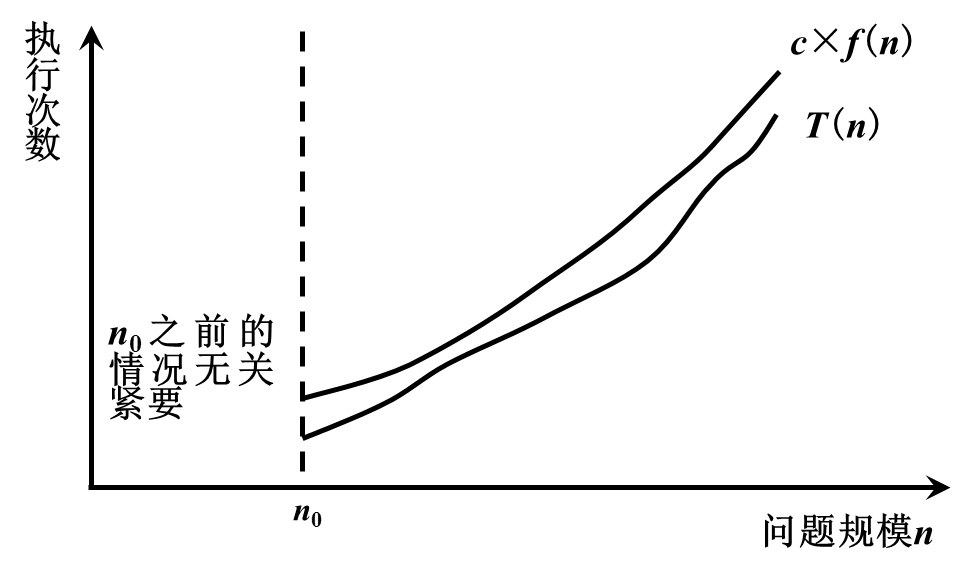
2、渐进下界记号-大Ω符号
若存在两个正的常数c和n0,对于任意n≥n0,都有T(n)≥c×g(n),则称T(n)=Ω(g(n))
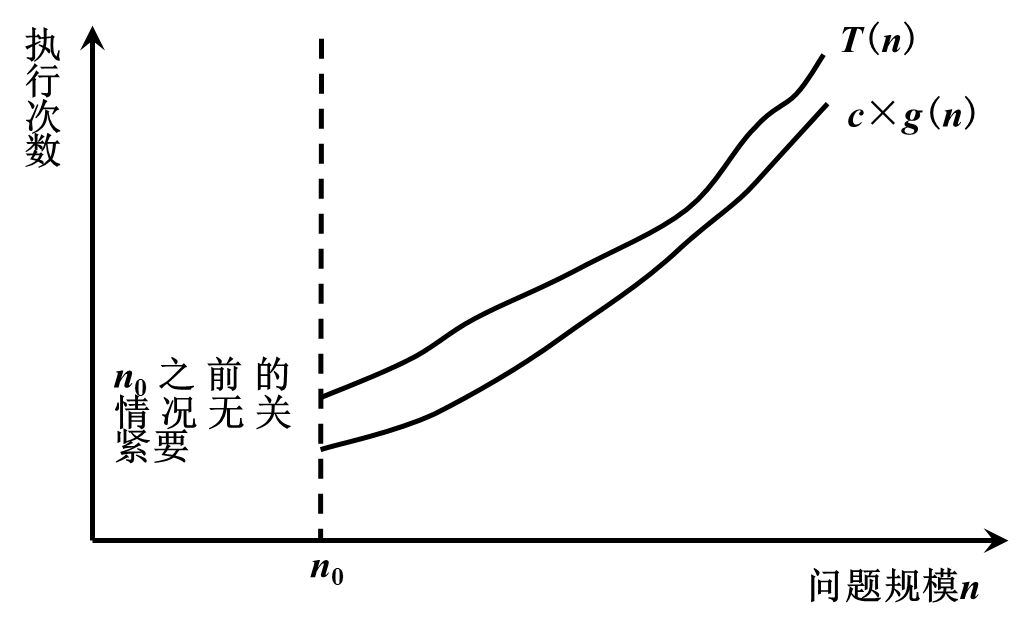
3、紧渐进界记号-Θ符号
若存在三个正的常数c1、c2和n0,对于任意n≥n0都有c1×f(n)≥T(n)≥c2×f(n),则称T(n)=Θ(f(n))
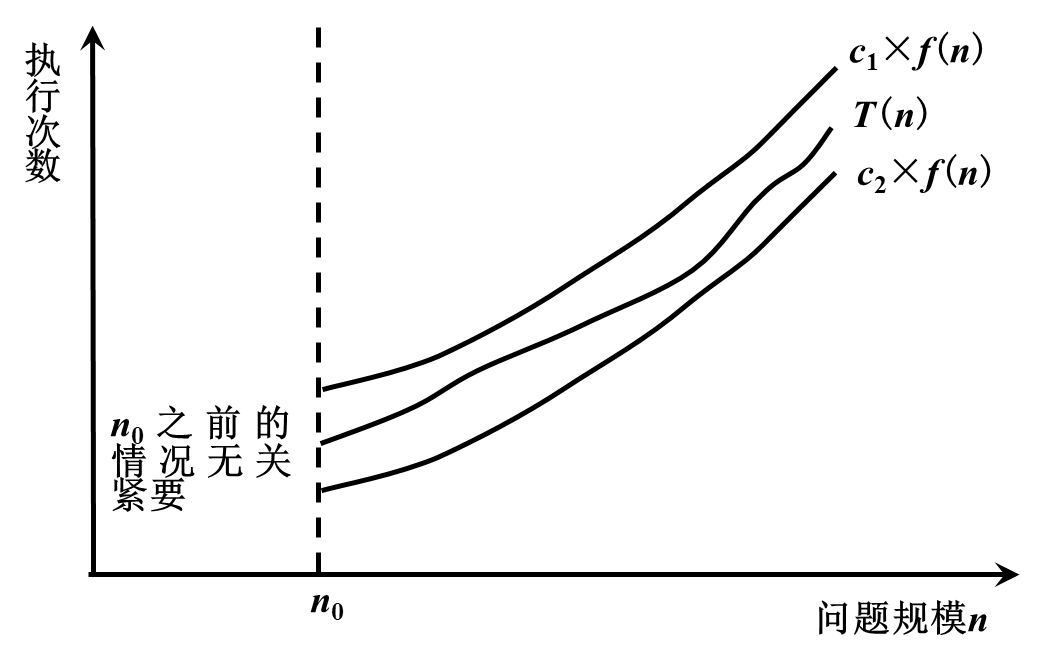
例: T(n)=5n2+8n+1
当n≥1时,5n2+8n+1≤5n2+8n+n=5n2+9n≤5n2+9n2≤14n2=O(n2)
当n≥1时,5n2+8n+1≥5n2=Ω(n2)
∴ 当n≥1时,14n2≥5n2+8n+1≥5n2
则:5n2+8n+1=Θ(n2)
定理:若T(n)=amnm +am-1nm-1 + … +a1n+a0(am>0),则有T(n)=O(nm)且T(n)=Ω(n m),因此,有T(n)=Θ(n m)。
4、非紧上界记号o
o(g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n0 >0使得对所有n≥n0有:0<f(n)<cg(n) }
等价于 f(n) / g(n) →0 ,当 n→∞。
5、非紧下界记号ω
ω(g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n0 >0使得对所有n> n0有:0 ≤ cg(n) < f(n) }
等价于 f(n) / g(n) →∞ ,当 n→∞。
6、渐近分析记号在等式和不等式中的意义
f(n)= Θ(g(n))的确切意义是:f(n) ∈ Θ(g(n))。
一般情况下,等式和不等式中的渐近记号Θ(g(n))表示Θ(g(n))中的某个函数。
例如:2n2 + 3n + 1 = 2n2 + Θ(n) 表示
2n2 +3n +1=2n2 + f(n),其中f(n) 是Θ(n)中某个函数。
等式和不等式中渐近记号O,o, Ω和ω的意义是类似的。
7、渐近分析中函数比较
f(n)= O(g(n)) ≈ a ≤ b;
f(n)= Ω(g(n)) ≈ a ≥ b;
f(n)= Θ(g(n)) ≈ a = b;
f(n)= o(g(n)) ≈ a < b;
f(n)= ω(g(n)) ≈ a > b.
8、渐近分析记号的若干性质
(1)传递性
f(n)= Θ(g(n)), g(n)= Θ(h(n)) → f(n)= Θ(h(n));
f(n)= O(g(n)), g(n)= O (h(n)) → f(n)= O (h(n));
f(n)= Ω(g(n)), g(n)= Ω (h(n)) → f(n)= Ω(h(n));
f(n)= o(g(n)), g(n)= o(h(n)) → f(n)= o(h(n));
f(n)= ω(g(n)), g(n)= ω(h(n)) → f(n)= ω(h(n));
(2)反身性
f(n)= Θ(f(n));
f(n)= O(f(n));
f(n)= ω(f(n)).
(3)对称性
f(n)= Θ(g(n)) ⇔ g(n)= Θ (f(n)) .
(4)互对称性
f(n)= O(g(n)) ⇔ g(n)= Ω (f(n)) ;
f(n)= o(g(n)) ⇔ g(n)= ω (f(n)) ;
(5)算术运算
O(f(n))+O(g(n)) = O(max{f(n),g(n)}) ;
O(f(n))+O(g(n)) = O(f(n)+g(n)) ;
O(f(n))*O(g(n)) = O(f(n)*g(n)) ;
O(cf(n)) = O(f(n)) ;
g(n)= O(f(n)) → O(f(n))+O(g(n)) = O(f(n)) 。
规则O(f(n))+O(g(n)) = O(max{f(n),g(n)}) 的证明:
对于任意f1(n) ∈ O(f(n)) ,存在正常数c1和自然数n1,使得对所有n≥ n1,有f1(n) ≤ c1f(n) 。
类似地,对于任意g1(n) ∈ O(g(n)) ,存在正常数c2和自然数n2,使得对所有n≥ n2,有g1(n) ≤ c2g(n) 。
令c3=max{c1, c2}, n3 =max{n1, n2},h(n)= max{f(n),g(n)} 。
则对所有的 n ≥ n3,有
f1(n) +g1(n) ≤ c1f(n) + c2g(n)
≤ c3f(n) + c3g(n)= c3(f(n) + g(n))
≤ c32 max{f(n),g(n)}
= 2c3h(n) = O(max{f(n),g(n)}) .
9、算法渐近复杂性分析中常用函数
(1)单调函数
单调递增:m ≤ n → f(m) ≤ f(n) ;
单调递减:m ≥ n → f(m) ≥ f(n);
严格单调递增:m < n → f(m) < f(n);
严格单调递减:m > n → f(m) > f(n).
(2)取整函数
⌊ x ⌋ :不大于x的最大整数;
⌈ x ⌉ :不小于x的最小整数。
取整函数的若干性质
x-1 < ⌊ x ⌋ ≤ x ≤ ⌈ x ⌉ < x+1;
⌊ n/2 ⌋ + ⌈ n/2 ⌉ = 整数n;
对于n ≥ 0,a,b>0,有:
⌈ ⌈ n/a ⌉ /b ⌉ = ⌈ n/ab ⌉ ;
⌊ ⌊ n/a ⌋ /b ⌋ = ⌊ n/ab ⌋ ;
⌈ a/b ⌉ ≤ (a+(b-1))/b;
⌊ a/b ⌋ ≥ (a-(b-1))/b;
f(x)= ⌊ x ⌋ , g(x)= ⌈ x ⌉ 为单调递增函数。
(3)多项式函数
p(n)= a0+a1n+a2n2+…+adnd; ad>0;
p(n) = Θ(nd);
f(n) = O(nk) ⇔ f(n)多项式有界;
f(n) = O(1) ⇔ f(n) ≤ c;
k ≥ d → p(n) = O(nk) ;
k ≤ d → p(n) = Ω(nk) ;
k > d → p(n) = o(nk) ;
k < d → p(n) = ω(nk) .
(4)指数函数
对于正整数m,n和实数a>0:
a0=1;
a1=a ;
a-1=1/a ;
(am)n = amn ;
(am)n = (an)m ;
aman = am+n ;
a>1 → an为单调递增函数;
a>1 →
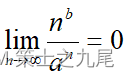
→ nb = o(an)
(5)对数函数
log n = log2n;
lg n = log10n;
ln n = logen;
logkn = (log n)k;
log log n = log(log n);
for a>0,b>0,c>0

(6)阶乘函数
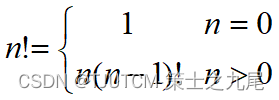
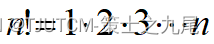
Stirling’s approximation
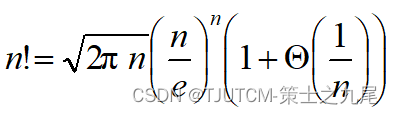
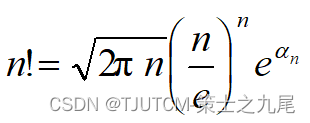

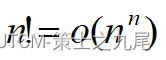
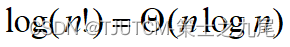
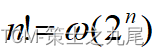
10、算法分析中常见的复杂性函数
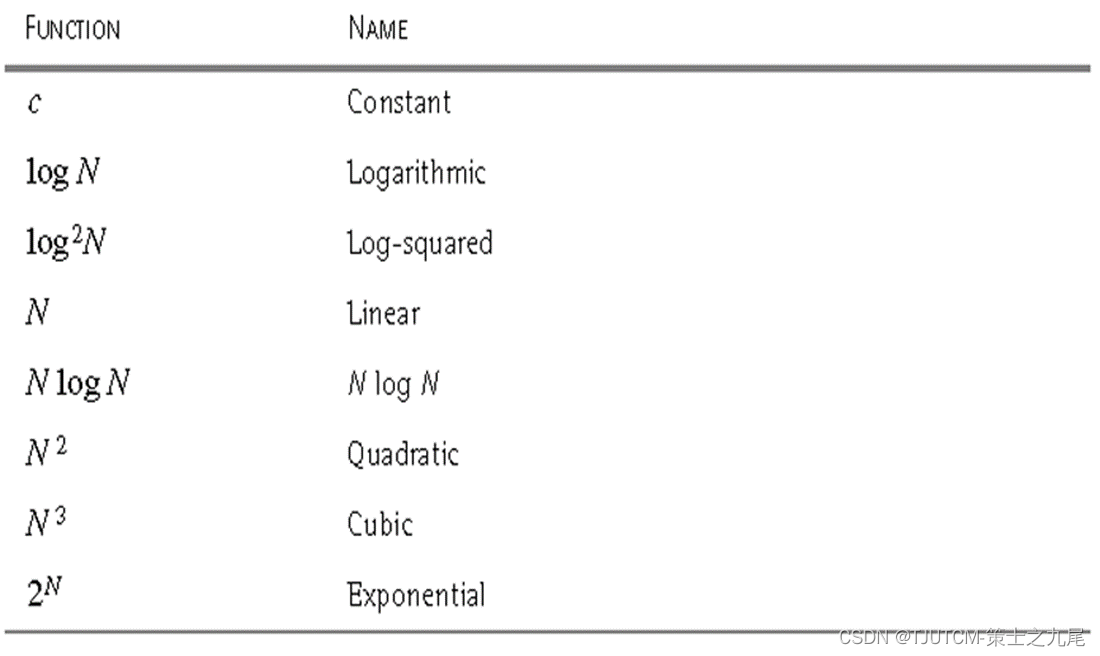
(1)小规模数据
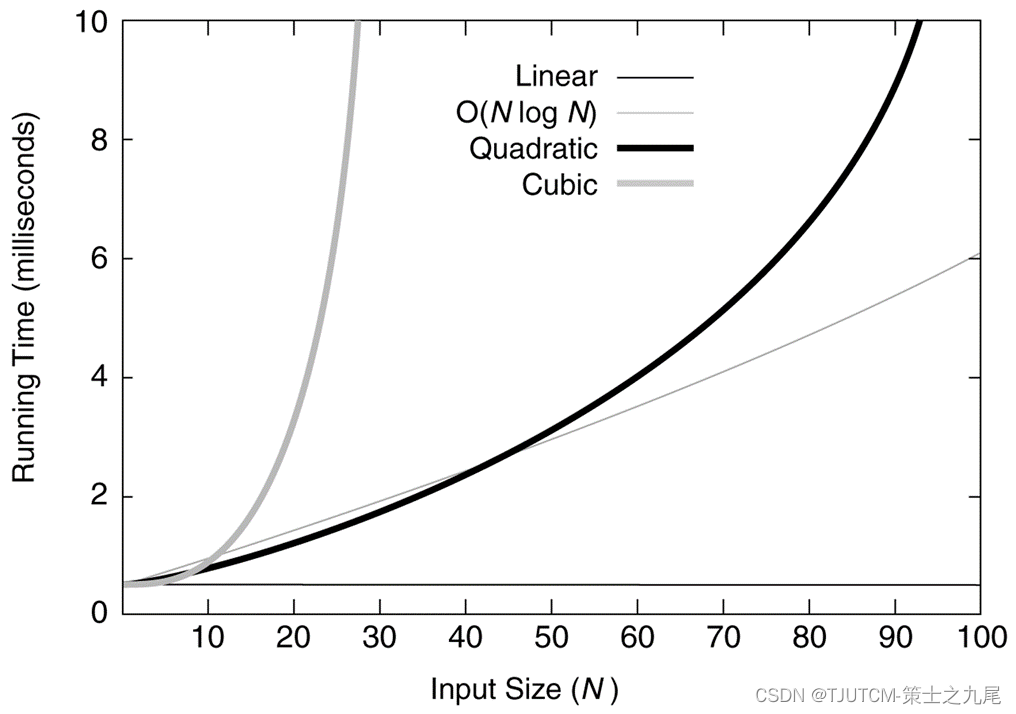
(2)中等规模数据
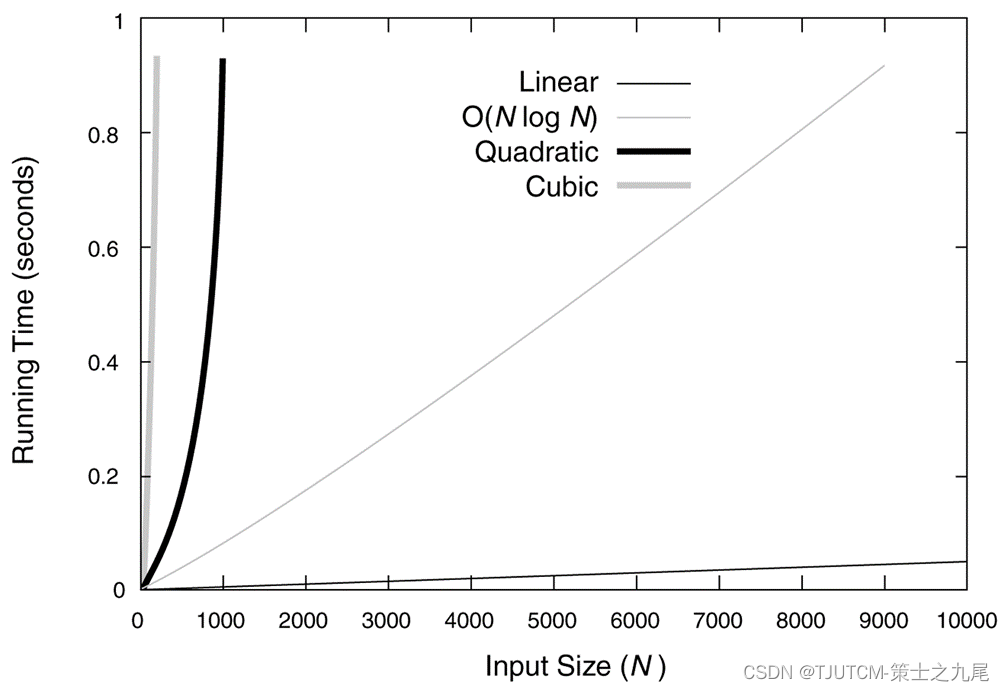
(3)算法分析方法
例:顺序搜索算法
template<class Type>
int seqSearch(Type *a, int n, Type k)
{
for(int i=0;i<n;i++)
if (a[i]==k) return i;
return -1;
}
(1)Tmax(n) = max{ T(I) | size(I)=n }=O(n)
(2)Tmin(n) = min { T(I) | size(I)=n }=O(1)
(3)在平均情况下,假设:
(a) 搜索成功的概率为p ( 0 ≤ p ≤ 1 );
(b) 在数组的每个位置i ( 0 ≤ i < n )搜索成功的概率相同,均为 p/n。
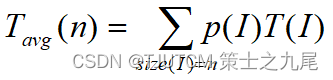
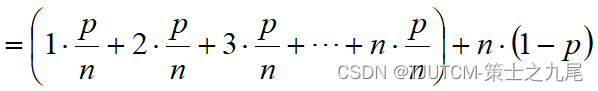
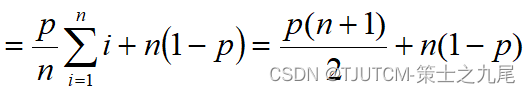
九、算法分析的基本法则
1、非递归算法:
(1)for / while 循环
循环体内计算时间*循环次数;
(2)嵌套循环
循环体内计算时间*所有循环次数;
(3)顺序语句
各语句计算时间相加;
(4)if-else语句
if语句计算时间和else语句计算时间的较大者。
2、最优算法
问题的计算时间下界为Ω(f(n)),则计算时间复杂性为O(f(n))的算法是最优算法。
例如,排序问题的计算时间下界为Ω(nlogn),计算时间复杂性为O(nlogn)的排序算法是最优算法。
堆排序算法是最优算法。