树
树的特点:不是简单的线性结构,但在确定某种次序之后,具有线性特征。对于树,它集成vector和list的优点,既可以快速插入、删除也可以快速查找。
递归定义
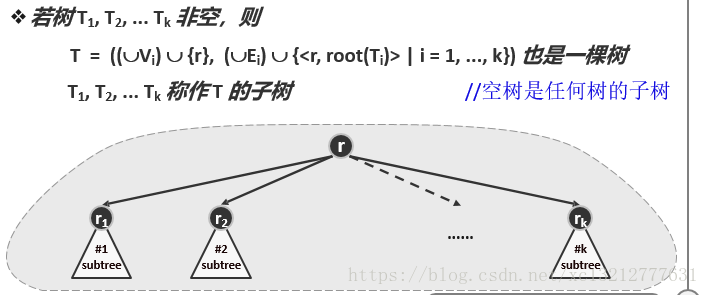
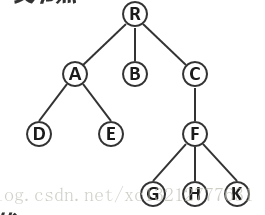
树是特殊的图T=(V,E),节点数|V|=n ,边数|E|=e。指定任一节点r属于V作为根后,T即称作有根树。
如:
若指定r=root(T),则
1、称ri 为 r 的孩子;称 r 为 ri 的父亲;r1, r2, …, rk 互称兄弟。
2、k 称为 r 的(出)度,记作 deg(r) = k
3、没有孩子的节点称作叶子,否则称为内部节点。
说明:
- 在一般的图中,度数被定义为“关联节点的数目”,故 所有节点度数总和 = m 条边对度数的总贡献 = 2m。
- 对于有根树,根节点度数不变,其它节点各少一度,故m = 所有节点度数的总和 = 减少度数的总和 = n‐1 对于树结构来说,节点数目与边数目相当,故 在衡量相关复杂度时,可以 n 作为参照
拓扑定义
首先要介绍一下图的相关定义。
路径:V 中的 k+1 个节点,通过 E 中的 k 条边首尾相联构成的序列D = {(v0, v1), (v1, v2), …… , (vk‐1, vk)};|D| = k称作路径长度。当vk = v0时构成环路。
节点之间均有路径称之为连通图,不包含任何的环路为无环图。
这里所说的连通性与无环性与树有什么关系呢?
树其实就是在无环和连通之间达到一种平衡的图。因为无环所以边数不会太大,又因为是连通的所以边数不会太少。即树可以保证,在杜绝环路的情况下使用尽可能多的边,在保证连通的情况下使用最少的边。即:
树 = 无环连通图 = 极小连通图 = 极大无环图
根据上述特征可得:任一节点V与根之间存在唯一路径path(v,r)=path(v)。
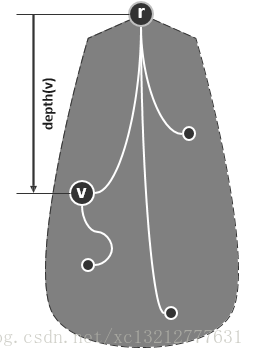
根据上述结论可以得到树的拓扑定义,首先给出下图:
有以下定义:
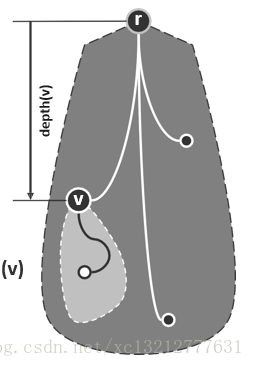
1、在以 r 为根的树 T 中,每一节点 v 都有一个非负的深度。depth(v)=|d(r,v)|,即从r通往v的路径长度,特别地,depth(r)=0。
2、沿d(r,v)与v相连的节点u称作v的父亲,u=parent(v);反过来,v称作u的孩子。除了根之外,每个节点的父亲唯一;同一节点的孩子互称兄弟。
3、d(r,v)上的每一节点,都是 v 的祖先。除 v 本身外的祖先,称作 v 的真祖先,v 是它们的后代。
4、在从 0 到 depth(v) 的每一深度上v都有唯一的祖先,因此depth(v) = |{v的真祖先}|。
5、节点 v 的所有后代也构成一棵树称作“T 中以 v 为根的子树”,记作 subtree(v)。没有真后代的节点,称作叶子,其对应的子树只含该节点。v的孩子总数,称作其度数记作deg(v)。
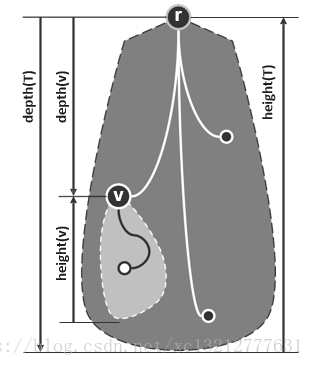
6、树 T 的高度 =T 中所有节点的最大深度height(T) = max{depth(v) | v属于V},约定:depth(空树) = ‐1;T 的深度:depth(T) = height(T)。
7、节点 v 的高度 =为以 v 为根的子树高度height(v) = height(subtree(v))
则:depth(v) + height(v) <= height(T)
存储结构
一般的,树中各节点的孩子数目并不确定。每个节点的孩子均不超过K个的有根树,称作K叉树。下面就此类树结构的表示与实现方法作简要介绍。
父节点表示法
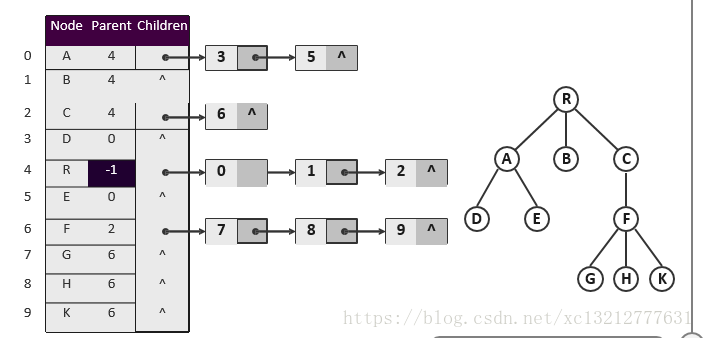
在多叉树中,根节点以外的任一节点有且仅有一个父节点。因此,可以将各节点组织为向量或者列表,其中每个元素除了保存节点本身的信息之外,还要保存节点的秩或位置。(数根指定一个虚构的父节点,以便同一判断)如下所示:
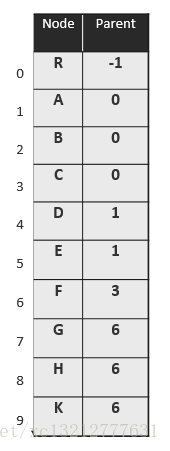
如此,所有向量或列表所占的空间总量为O(n),线性正比于节点总数n。时间方面,仅需常数时间,就可以确定任一节点的父节点;反过来,孩子节点的查找要花费O(n)时间访问所有的节点。
因此要考虑,如何加快孩子节点的查找?
孩子节点表示法
如果想要注重孩子节点的快速定位,令各节点将其所有的孩子组织为一个向量或列表。
即:1、每个节点的孩子构成一个线性(单链)表;2、所有链表的头结点构成一个线性(顺序)表。
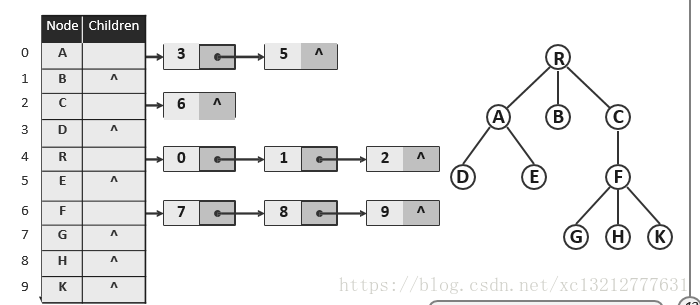
如此,对于拥有r个孩子的节点,可以在O(r+1)列举出其所有的孩子。但是查找父节点却很慢。
父节点+孩子节点表示法
上述父节点表示法和孩子节点表示法各有所长,但也各有所短。为了综合二者的优势,消除缺点。我们可以让各个节点既记录父节点,同时维护一个序列保存孩子节点。如下:
虽然可以高效的兼顾对父节点和孩子节点的定位,但在节点插入与删除操作频繁的场合,为了动态地维护和更新树的拓扑结构,不得不反复地遍历和调整一些节点所对应的孩子序列。
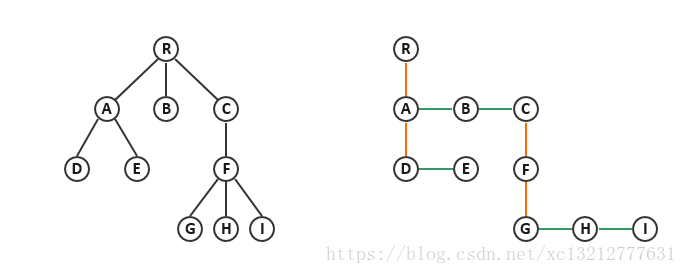
因此,可以采用支持高效动态调整的二叉树结构。首先,要建立从多叉树到二叉树的转换关系,并在此转换意义下任一多叉树都等价于某颗二叉树。我们只需要给多叉树增加一个约束条件,同一节点的孩子之间必须具有某一线性次序。
说明:经:firstChild(指向第一个孩子) 纬:nextSibling(指向下一个兄弟)
性能:访问x的第i个孩子:O(1+i)=O(i);