对偶问题:也是QP问题。对偶问题,几乎与空间的维度无关。
alpha:原来拉格朗日乘子。 条件数量/变数数量都为N,好像跟维度d quota无关。 d quota跑到Q矩阵中去了,因为Qnm是由zTz计算出来。d quota很大时,就是这个算法的瓶颈所在。 能否把该步骤计算的更快一点呢?
先做转换再做内积,则计算量很大。 能不能把这两个步骤合起来,算的快一点呢?
多项式转换:原来的多项式拿来,计算出各种不同多项式的排列组合。
看起来,经过计算,可以有d^2的计算量降低到d的计算量。
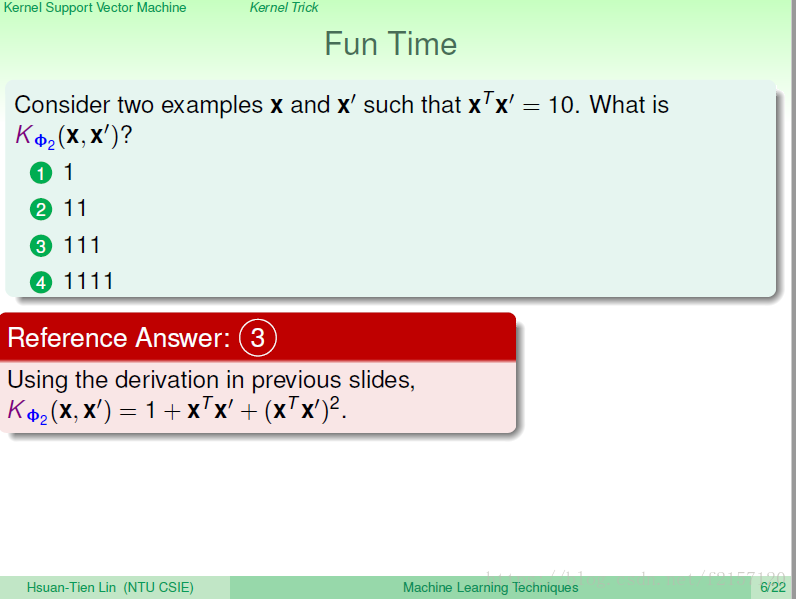
z与z的内积:kernel function作用于xn
计算b的公式不需要计算z空间,只需要kernel与alpha即可。
用kernel, alpha,b来最优化svm,看起来所有的计算都只需要x,不需要z,看起来好像可以很有效率的做法,避免与d quota的维度制约。
有多少个svm,就有多少个kernel evaluation
只需要support vector,就可以实现对未来的预测
有很多不同的二次多项式可用。
将1次转换的前面都乘以根号2,当算乘法时,就会跑出一个2来。
1次项前面乘以根号2gama,二次项前面乘以gama,转换后的..... 看起来是一个(a+b)的平方的展开
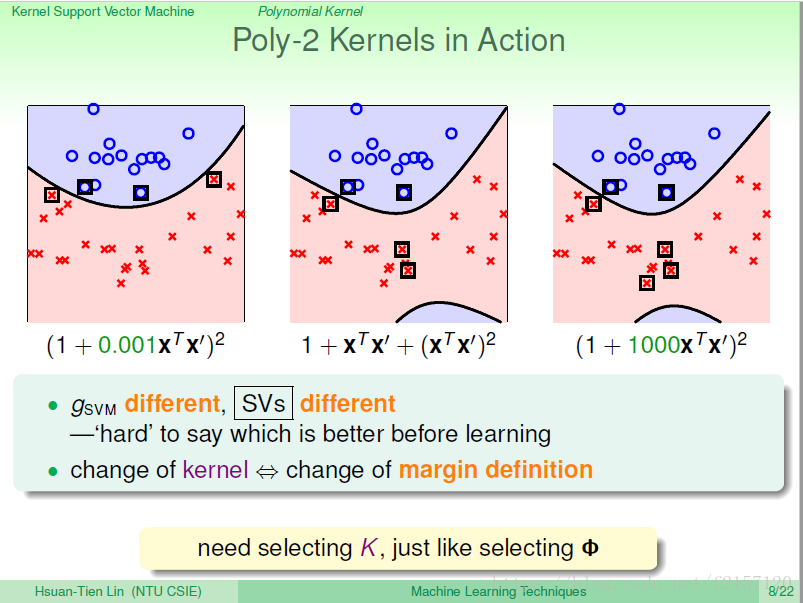
不同的转化,同样的空间,算出来的形式也会不同。
不同的内积,代表不同的距离,不同的距离会决定不同的margin,不同的几何特性,可能不同的边界
不同的参数,得到的边界不同,很难说那个更好。
Q次方的多项式kernel。
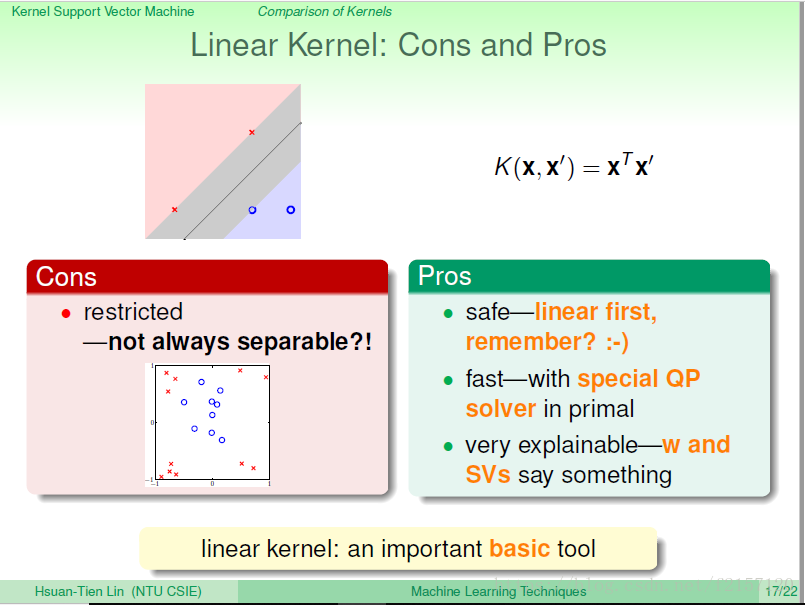
linear kernel:只用原来的x在x空间做内积的动作,对应的是原来的data,什么转换也没有做
linear kernel,搞不好也不用做对偶转换,用原来的SVM问题,求解得到一个很胖的边界就结束。
如果linear可以做的很好,就没必要做polynominal的转换。当做不好,做转换才安全(会得到更好的解)
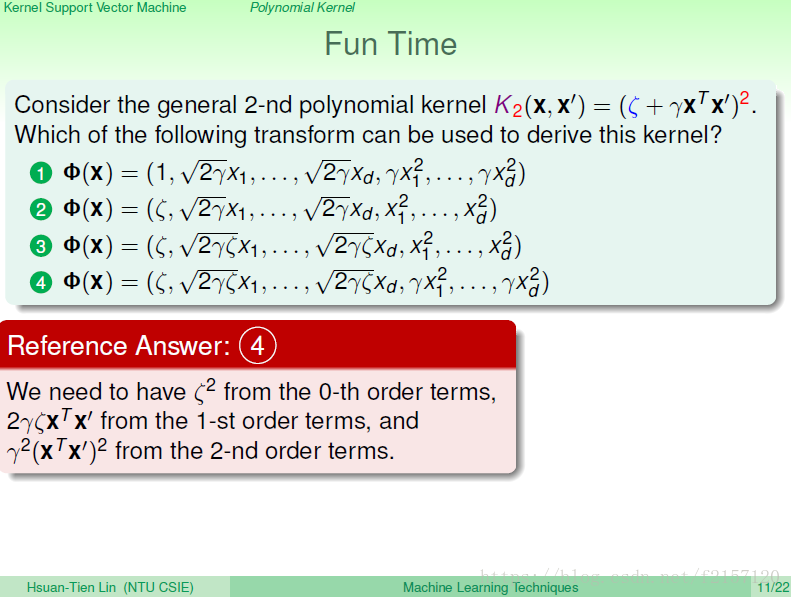
需要zeta在常数转换的地方左除一个zeta 平方还,在二次转换的地方左除一个gama平方来,最后才能得到相对应的kernel
高斯函数:里面藏了无限多维的kernel
Kernel: k是高斯函数,中心在support vector上的高斯函数的线性组合。
高斯函数用SVM算出来的解,就对应到将原来的data映射到无限多维的空间,在那个空间里面找出一个最胖的边界,做一样的事情的化,就可以得到好的分类。
看过程的话,就属于一堆在中心support vector上的高斯函数的线性组合。 因为这个特性,通常也称为RBF,Radio:长得像高斯,从某个中心开始向外,长得弯弯曲曲的函数。 Basic Function:拿来做线性组合。
表现方式:那些support vector,用哪些系数线性组合起来。
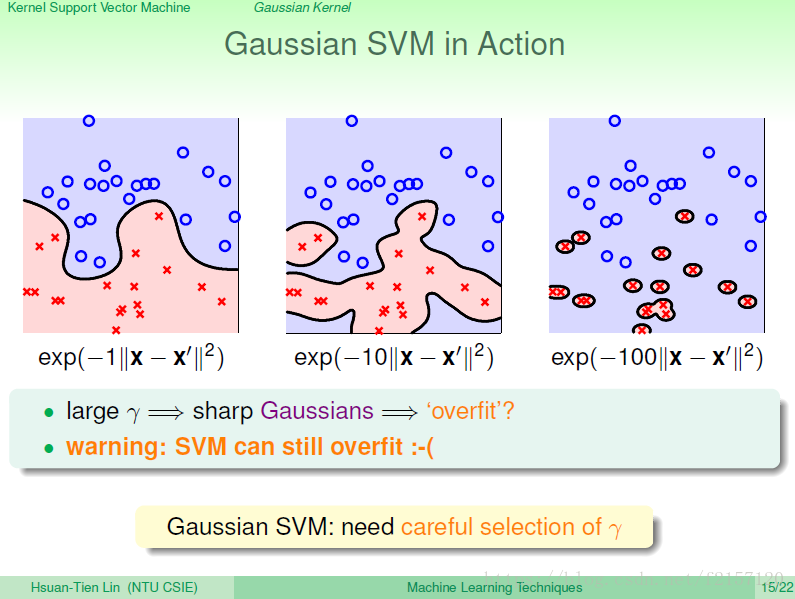
gama,从1,到10,到100,逐渐overfit。
即使有large margin,如果gama使用不好,仍然可能会导致overfit
Gama的选择要谨慎,不建议选太大的Gama
只看每个资料,x与x pron是不是一样,一样为1,不一样为0,对测量误差的容忍度非常低。
最简单的是linerar kernel:不做任何转换。 硬要解kernel,就是将原来的data丢进去。
Polynomial Kernel:缺点是不太好算,大的Q不太好用,数值表达比较复杂。
有Q,gama,eta等好几个参数要选择,不太好选择。通常,只适用于小的Q。搞不好,不做polynomial转换计算会更快
Guassian的范围:0~1之间,相比较polynomial kernel,范围较固定。
参数只有gama,参数选择会容易一点。
缺点:从来都不会算出无限多维的w,难于解释。--》不完全知道你的资料是如何算出来的。
把Qd计算出来,可能会慢一点。
如果参数选不好,也可能会导致overfit
内积:本来就是一种相似性
Kernel是一种相似性,代表向量内积在z空间里面的相似性。
如果是kernel,必须是对称的,因为向量内积就是对称的。
两个z矩阵的相乘ZZT 一定会是半正定的。
这个条件,不但是必要的,还是充分的。(对称,半正定),证明比较困难。
K矩阵不半正定。