目录
一. 微分代数方程求解
例题1
初始条件:
求数值解:
解:
①方法1求解
矩阵形式表示该微分代数方程:
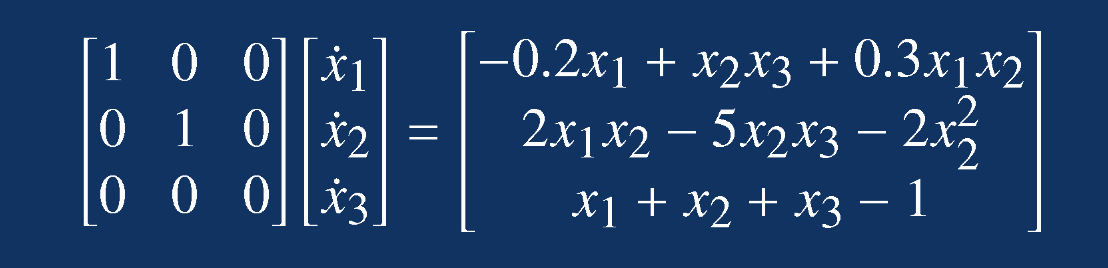
(1)函数文件
function dx=c7eqdae(t,x)
dx=[-0.2*x(1)+x(2)*x(3)+0.3*x(1)*x(2);2*x(1)*x(2)-5*x(2)*x(3)-...
2*x(2)*x(2);x(1)+x(2)+x(3)-1];(2)主运行文件
clc;clear;
M=[1 0 0;0 1 0; 0 0 0];
options=odeset;
options.Mass=M; %Mass微分代数方程中的质量矩阵(控制参数)
x0=[0.8;0.1;0.1];
[t,x]=ode15s(@c7eqdae,[0,20],x0,options);
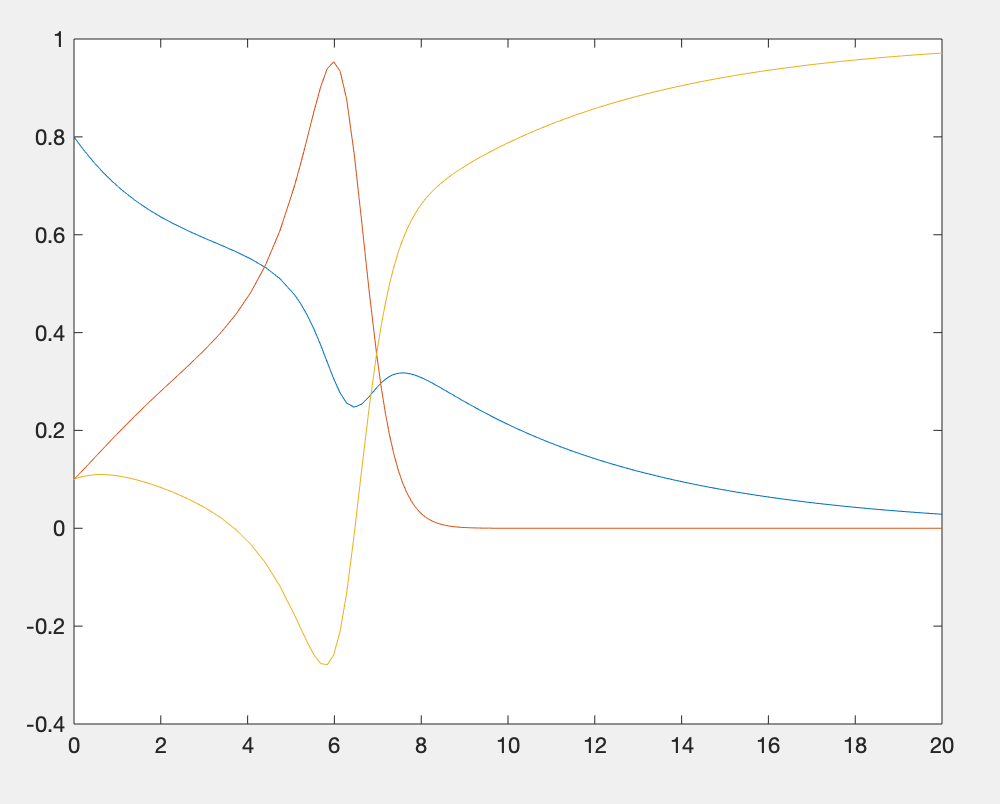
plot(t,x)
运行结果:

②方法2:转换成常微分方程求解
从约束式子可得:
代入原式子可得:
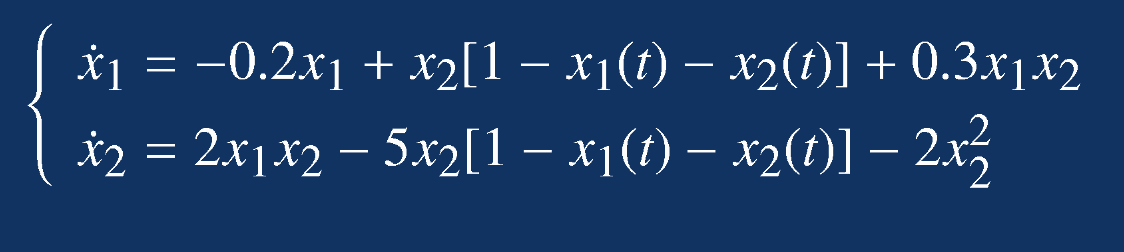
(1)函数文件
function dx=c7eqdae1(t,x)
dx=[-0.2*x(1)+x(2)*(1-x(1)-x(2))+0.3*x(1)*x(2);...
2*x(1)*x(2)-5*x(2)*(1-x(1)-x(2))-2*x(2)*x(2)];(2)主运行文件
clc;clear;
x0=[0.8;0.1];
[t1,x1]=ode45('c7eqdae1',[0,20],x0);
plot(t1,x1,t1,1-sum(x1'))运行结果:
二. 全隐式微分方程
ode15i可解算全隐式微风方程。格式:
%格式1
[t,y]=ode15i(odefun,tspan,y0,yp0,options)
%格式2
[y0_new,yp0_new]=decic(odefun,t0,y0,fixed_y0,yp0,fixed_yp0,options)
%decic 为ode15i计算一致的初始条件可以使用以下命令看具体函数细节:
edit hbldae.m
edit ihbldae.m三. 延迟微分方程求解
延迟微分方程组的一般形式如下:

隐式Runge-Kutta算法dde23()格式如下:
sol=dde23(f1,τ,f2,[t0,tf])
%sol为结构体数据,sol.x为时间向量,sol.y为状态向量
%f1为延迟微分方程
%τ=[τ1,···,τn]
%f2为t≤t0时的状态变量值函数例题2
求延迟微分方程组的数值解:
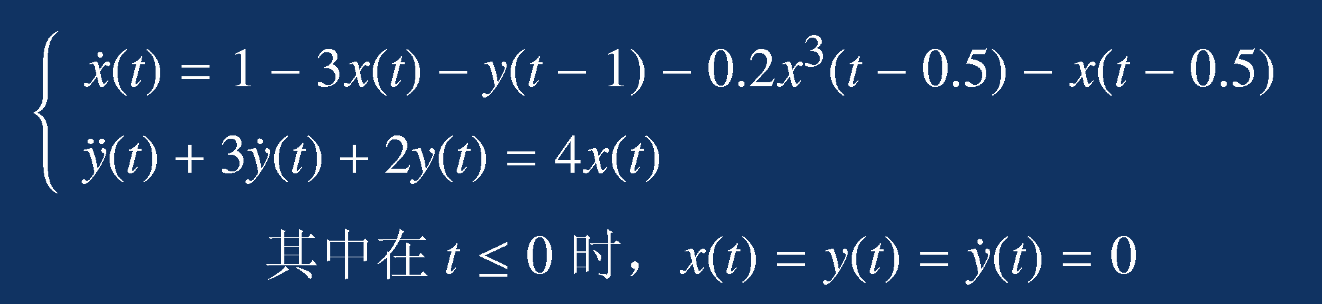
解:
选择状态变量:
得出一阶微分方程组:
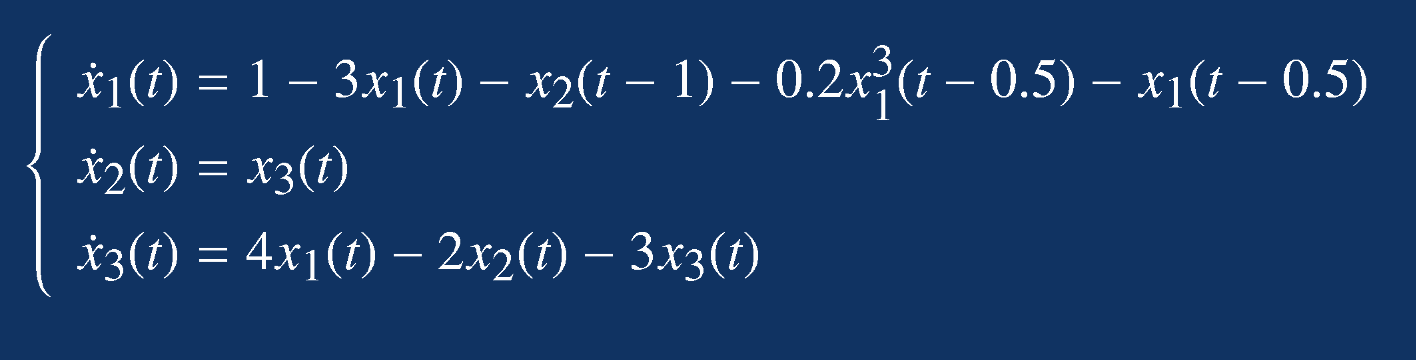
定义两个时间常数:
(1)编写函数
function dx=c7exdde(t,x,z)
xlag1=z(:,1); %第一列表示提取x(τ1)
xlag2=z(:,2);
dx=[1-3*x(1)-xlag1(2)-0.2*xlag2(1)^3-xlag2(1);...
x(3);4*x(1)-2*x(2)-3*x(3)];
(2)主运行文件
clc;clear;
lags=[1 0.5];
tx=dde23('c7exdde',lags,zeros(3,1),[0,10]);
plot(tx.x,tx.y(2,:)) %与ode45()等返回的x矩阵不一样,这是按行排列的运行结果:
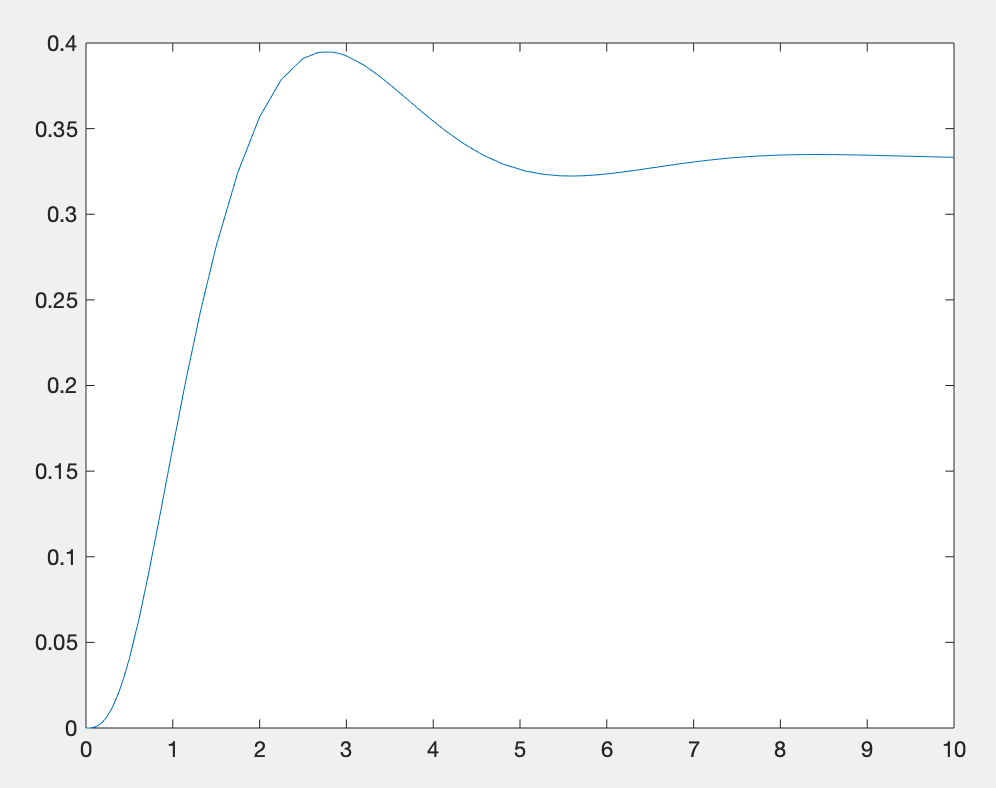
也可以调用以下命令来查看函数的具体信息:
edit ddex1
%具体的例子,编辑器的代码另外边值问题的也可以利用计算机来求解
二阶微分方程的边值问题的数学描述如下:
给定区间[a;b]上研究该方程的解,且在这两个边界条件下,满足: