一. 单个高阶常微分方程

例题1

二. 高阶常微分方程组

例题2

一. 单个高阶常微分方程

一个高阶常微分方程的一般形式如下：

$y^{(n)}=f(t,y,\dot y,\cdots,y^{(n-1)})$

输出变量y(t)的各阶导数初始值为如下：

$y(0),\dot y(0),\cdots,y^{(n-1)}(0)$

选择一组状态变量如下：

$x_1=y,x_2=\dot y,\cdots,x_n=y^{(n-1)}$

原高阶常微分方程模型可以变换为如下：

$\begin{cases} \dot x_1=x_2\\ \dot x_2=x_3\\ \quad \vdots\\x_n=f(t,x_1,x_2,\cdots,x_n) \end{}$

初值转换为如下：

$x_1(0)=y(0),x_2(0)=\dot y(0),\cdots,x_n(0)=y^{(n-1)}(0)$

例题1

已知边界值如下：

$y(0)=-0.2,y'(0)=-0.7$

用数值的方法求Van der Pol方程的解，如下：

$\ddot y+\mu(y^2-1)\dot y+y=0$

解：

首先做一个小小的转变：

$x_1=y,\quad x_2=y'$

范德坡方程的函数描述如下：

function y=vdp_eq(t,x,flag,mu)
y=[x(2);-mu*(x(1)^2-1)*x(2)-x(1)];

clc;clear;

x0=[-0.2,-0.7];
t_final=20;

mu=1;
[t1,y1]=ode45('vdp_eq',[0,t_final],x0,[],mu);

mu=2;
[t2,y2]=ode45('vdp_eq',[0,t_final],x0,[],mu);

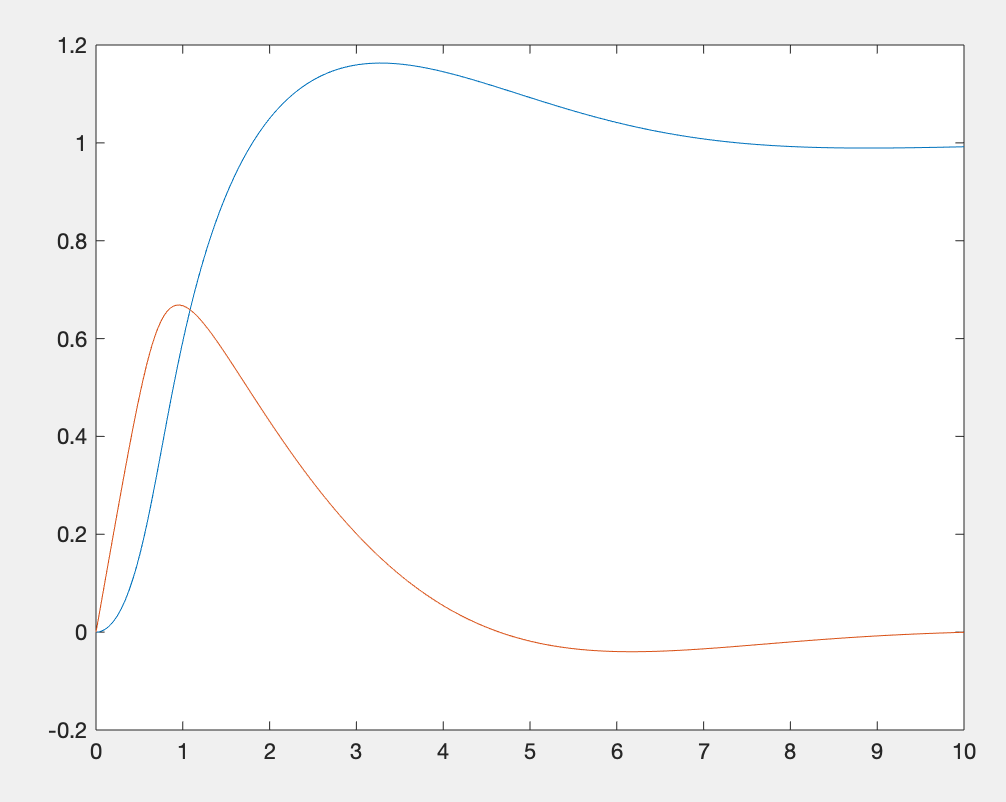
plot(t1,y1,t2,y2,':')
figure;
plot(y1(:,1),y1(:,2),y2(:,1),y2(:,2),':')

运行结果：

实际上，由于变步长所采用的步长过小，所需时间较长，会导致输出的y矩阵过大，会超出计算机存储空间容量。此时就不适合用ode45()函数来求解，可以用刚性方程求解算法ode15s()。

二. 高阶常微分方程组

高阶常微分方程的通式如下：

选择状态变量，如下：

于是，原方程组就可以变成如下形式：

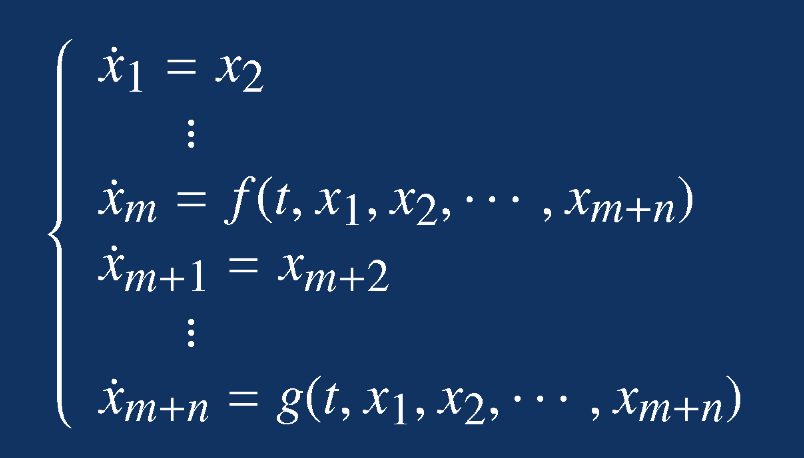
此过程的主题思想就是高阶变一阶，以方便使用ode 45函数。

例题2

解：

选择一组状态变量，如下：

$x_1=x,x_2=\dot x,x_3=y,x_4=\dot y$

由此得出一阶常微分方程组，如下：

此题MATLAB有两个文件。

（1）函数文件

function dx=apolloeq(t,x)
mu=1/82.45;
mu1=1-mu;
r1=sqrt((x(1)+mu)^2+x(3)^2);
r2=sqrt((x(1)-mu1)^2+x(3)^2);
dx=[x(2);
    2*x(4)+x(1)-mu1*(x(1)+mu)/r1^3-mu*(x(1)-mu1)/r2^3;
    x(4);
    -2*x(2)+x(3)-mu1*x(3)/r1^3-mu*x(3)/r2^3];

（2）主运行文件

clc;clear;
x0=[1.2;0;0;-1.04935751];
options=odeset;options.RelTol=1e-6;
[t1,y1]=ode45('apolloeq',[0,20],x0,options);
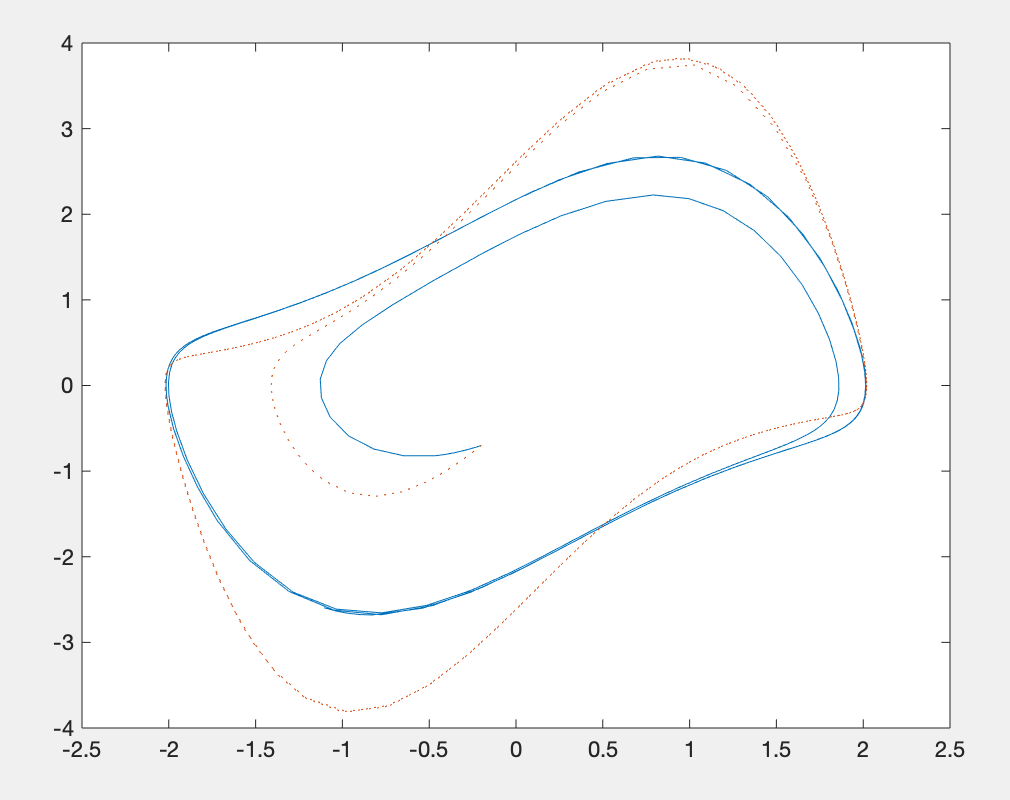
plot(y1(:,1),y1(:,3))

运行结果：

三. 刚性微分方程

刚性微分方程是一类特殊的常微分方程，其中一些解变化缓慢，另一些变化快，且两者相差悬殊。此时可用ode15s()函数求解，该函数的调用格式与ode45()完全一样。如下：

[t,x]=ode15s(Fun,[t0,tf],x0,options,p1,p2,···)

例题3

求解 $\mu=1000$ 时的Van der Pol方程的数值解。

$\ddot y+\mu(y^2-1)\dot y+y=0$

解：

此题有两个文件。

（1）微分描述文件

function y=vdp_eq(t,x,flag,mu)
y=[x(2);-mu*(x(1)^2-1)*x(2)-x(1)];

（2）主运行文件

clc;clear;

%计算范德坡方程
h_opt=odeset;h_opt.RelTol=1e-6;
x0=[2;0];
t_final=3000;
mu=1000;
[t,y]=ode15s('vdp_eq',[0,t_final],x0,h_opt,mu);
plot(t,y(:,1));
figure,
plot(t,y(:,2))

运行结果：

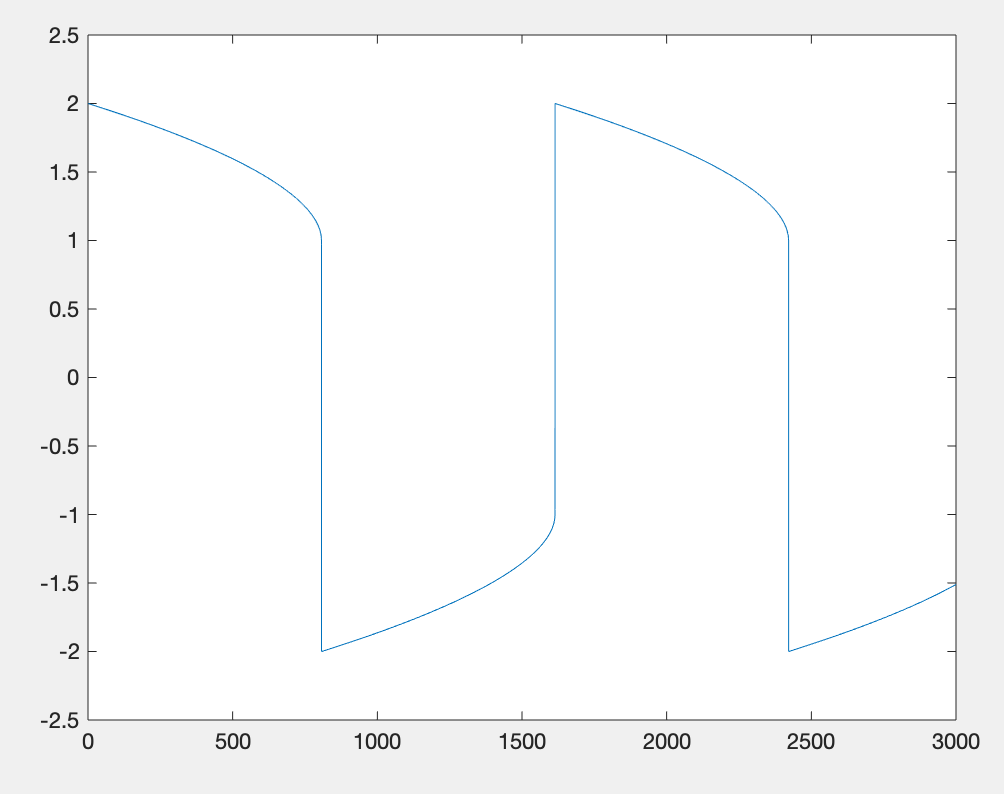
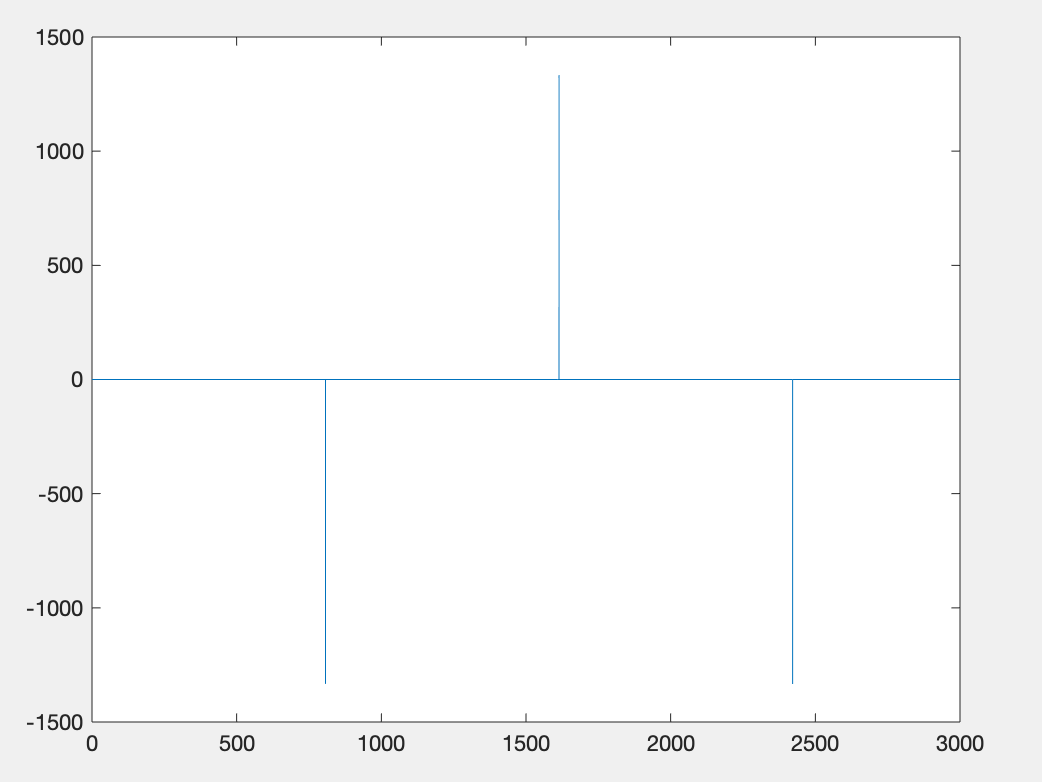
第一个曲线变化较为平滑，第二个曲线在某些点上变化较快。

例题4

该题求数值解，初值为如下：

$y_1(0)=0,y_2(0)=1$

计算区间为 $t\in (0,100)$

原微分方程如下：

$\begin{cases}\dot y_1=0.04(1-y_1)-(1-y_2)y_1+0.0001(1-y_2)^2\\ \dot y_2=-10^4y_1+3000(1-y_2)^2 \end{}$

解：

(1)函数文件

%定义函数
function dy=c7exstf(t,y)
dy=[0.04*(1-y(1))-(1-y(2))*y(1)+0.0001*(1-y(2))^2;...
    -10^4*y(1)+3000*(1-y(2))^2];

（2）主运行文件

clc;clear;

%方法一
[t2,y2]=ode45('c7exstf',[0,100],[0;1]);
plot(t2,y2)
format long
step1=[min(diff(t2)),max(diff(t2))] %步长分析
figure,
plot(t2(1:end-1),diff(t2))

%方法二：用ode15s()代替ode45()
opt=odeset;opt.RelTol=1e-6;
[t1,y1]=ode15s('c7exstf',[0,100],[0;1],opt);
figure,
plot(t1,y1)
figure,
plot(t1(1:end-1),diff(t1))

运行结果：
step1 = 0.000222206938844 0.002149717871840

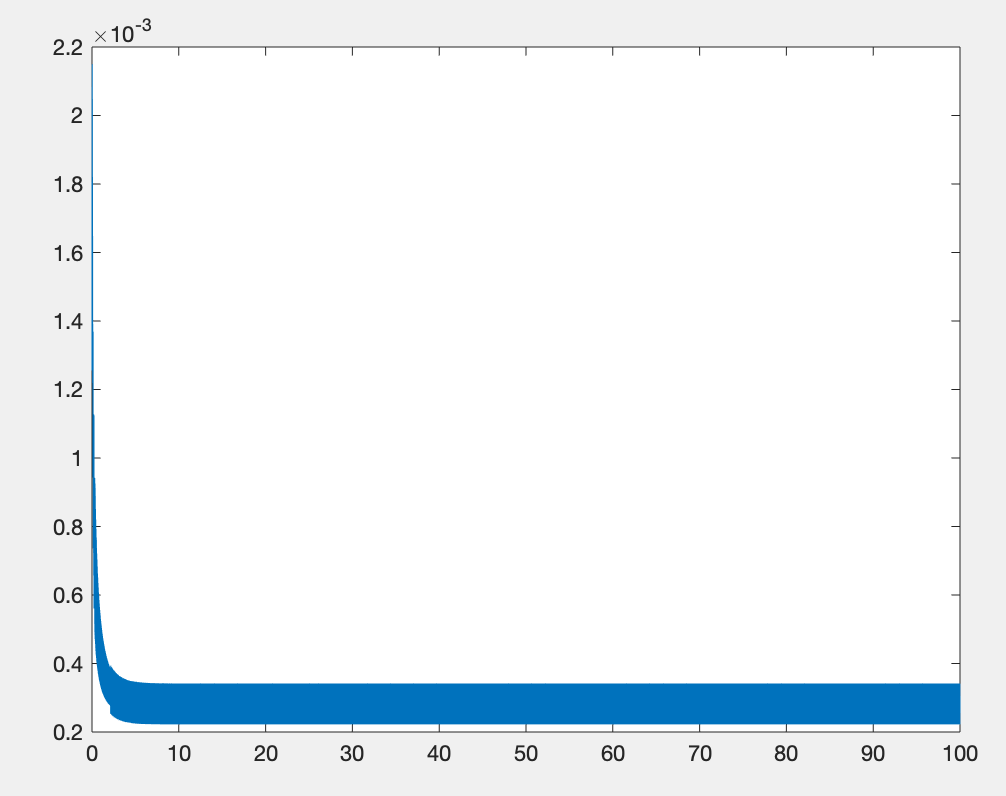
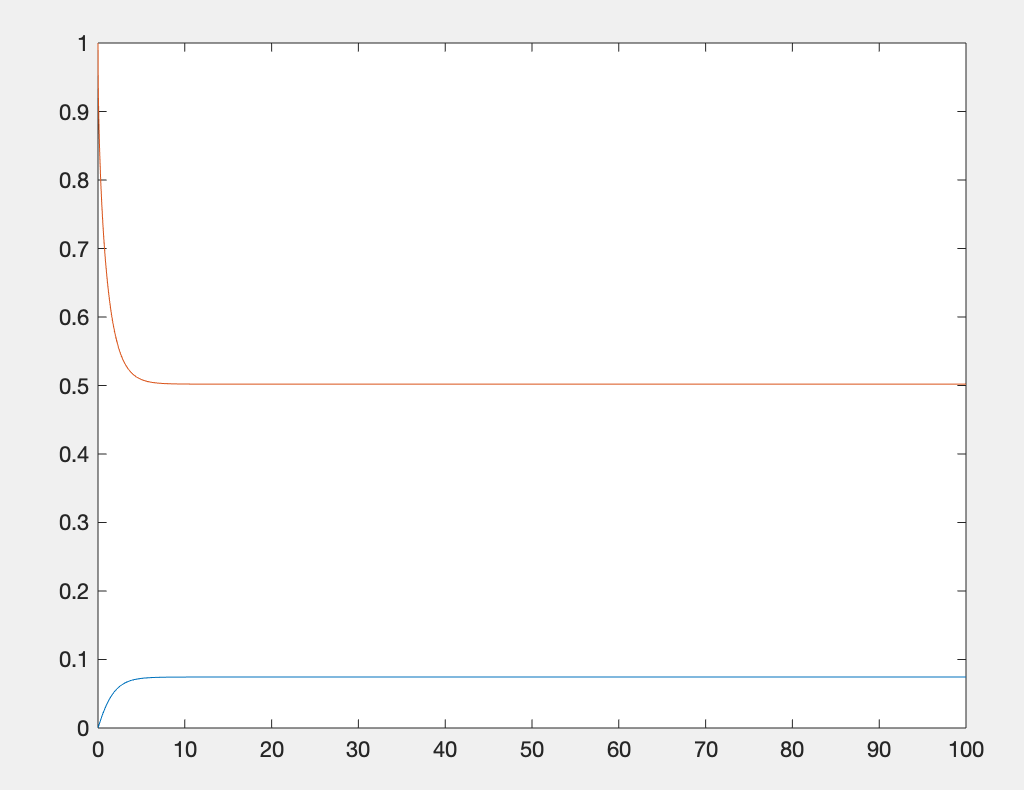
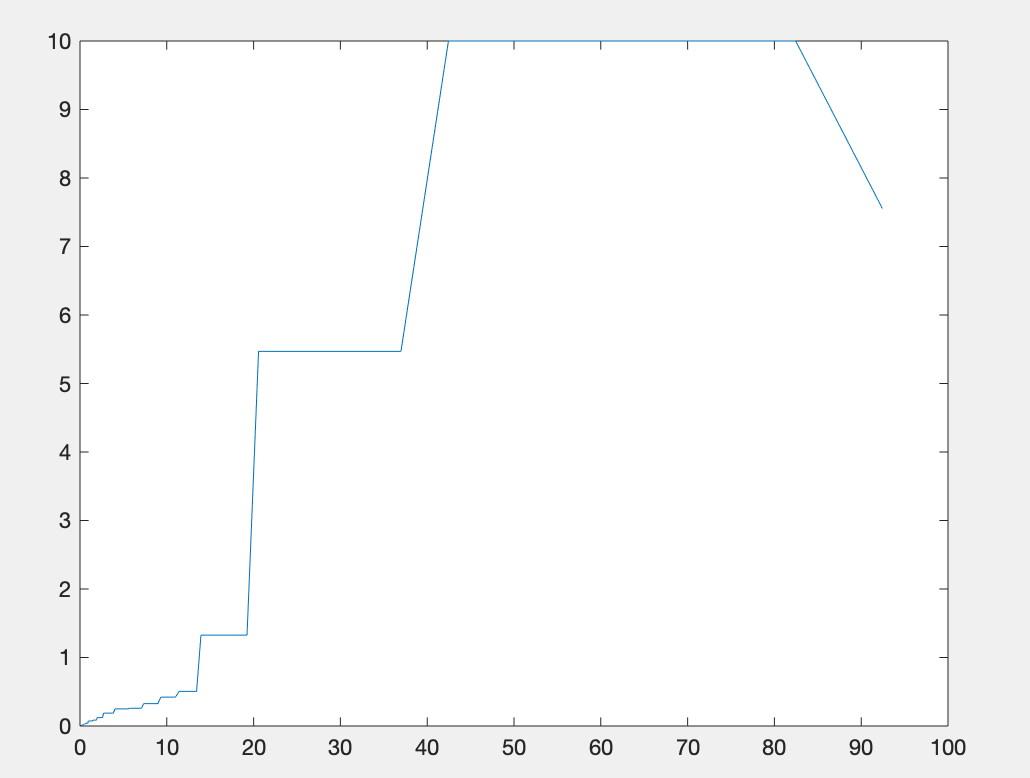
四. 隐式微分方程

隐式微分方程是不能转为显式常微分方程组的方程。

例题5

已知 $x_1(0)=x_2(0)=0$ ，求以下方程的数值解。

$\begin{cases}sinx_1\dot x_1+cosx_2\dot x_2+x_1=1\\-cosx_2\dot x_1+sinx_1\dot x_2+x_2=0 \end{}$

解：

令 $x=[x_1,x_2]^T$ ，原方程改写成：

$A(x)\dot x=B(x)$

其中A(x)与B(x)为如下：

$A(x)=\begin{bmatrix}sinx_1&cosx_2\\-cosx_2&sinx_1 \end{},\quad B(x)=\begin{bmatrix}1-x_1\\-x_2 \end{}$

B(x)为右端项。

（1）函数文件

function dx=c7ximp(t,x)
A=[sin(x(1)) cos(x(2));-cos(x(2)) sin(x(1))];
B=[1-x(1);-x(2)];
dx=inv(A)*B;

（2）主运行文件

clc;clear;
%求解
opt=odeset;opt.RelTol=1e-6;
[t,x]=ode45('c7ximp',[0,10],[0;0],opt);
plot(t,x) %变步长

运行结果：

基于MATLAB的高阶常微分方程组求解（附完整代码）

一. 单个高阶常微分方程

例题1

二. 高阶常微分方程组

例题2

三. 刚性微分方程

例题3

例题4

四. 隐式微分方程

例题5

猜你喜欢