1：缩放
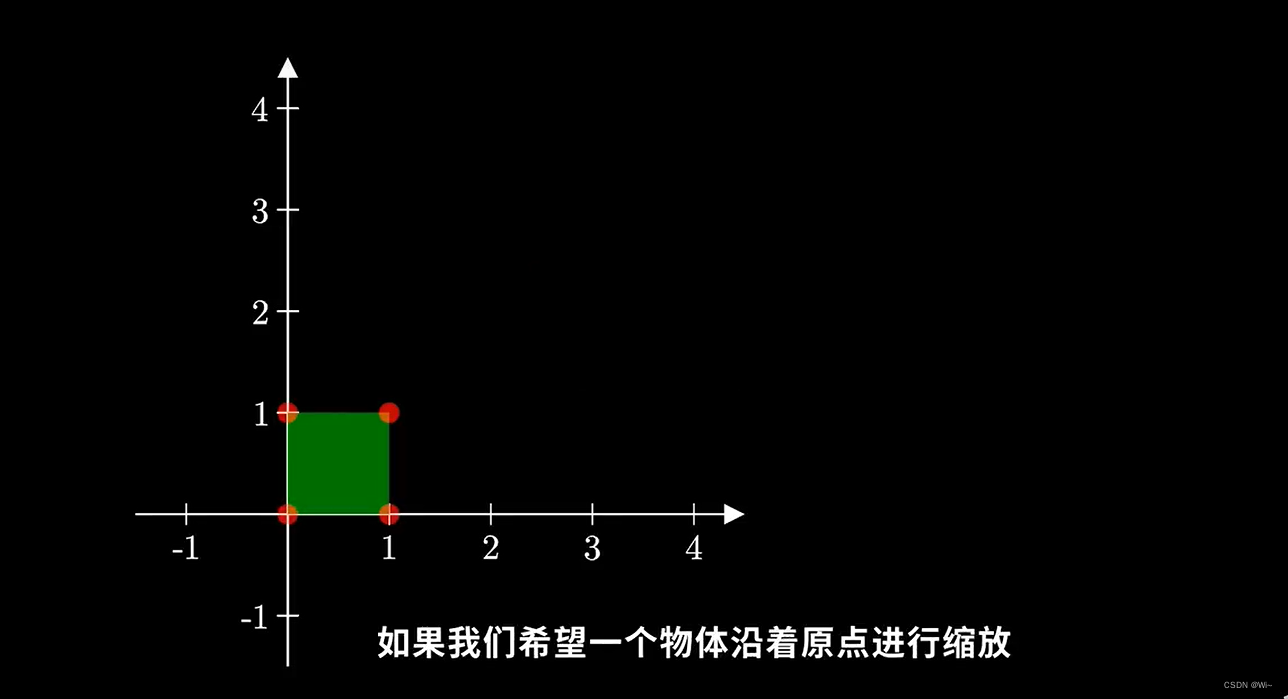
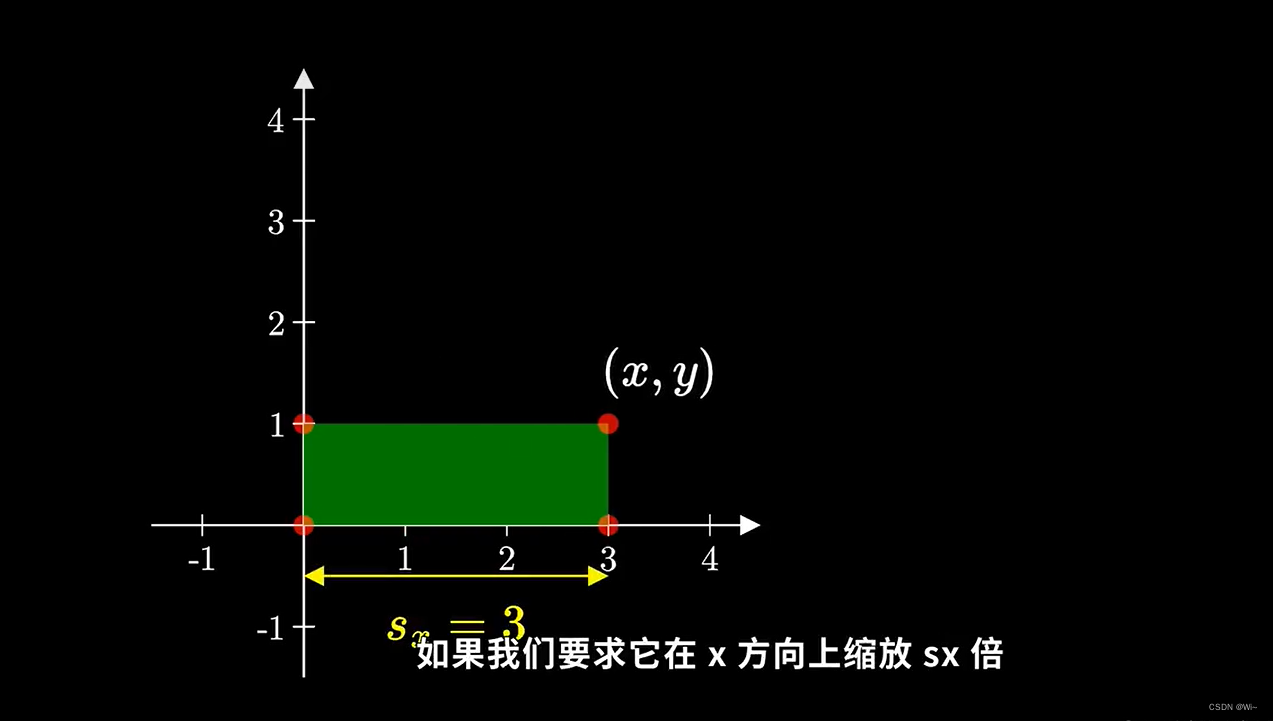
假设每一个顶点的坐标为(x, y)，如果我们要求它在x方向上缩放sx倍
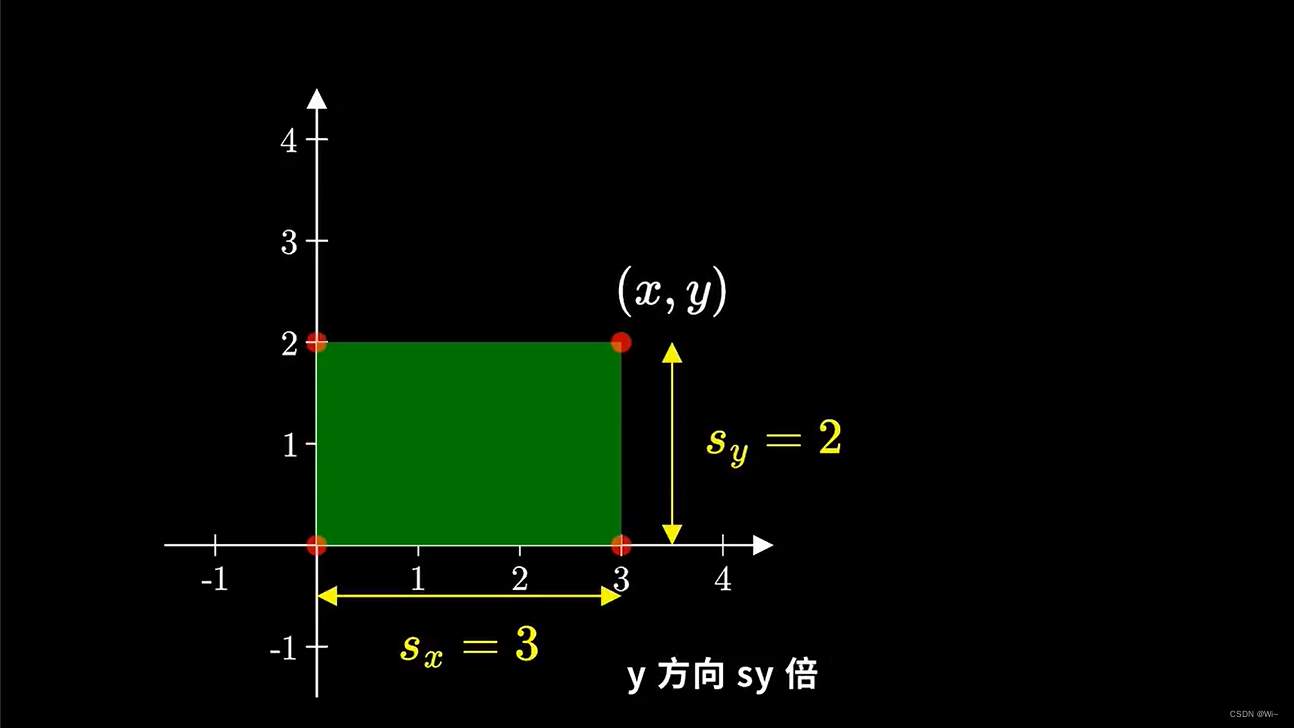
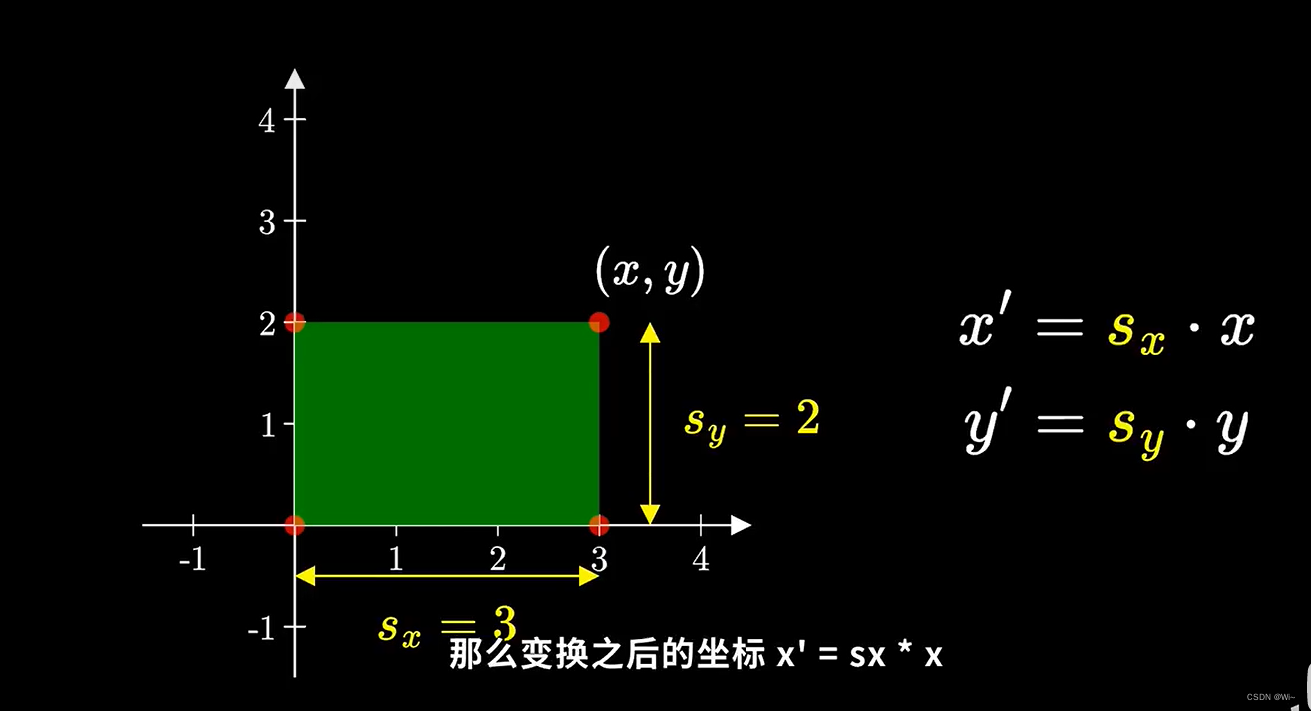
y方向sy倍，那么变换之后的坐标：（x’ = sx*x ） （y’ = sy *y）
2：平移
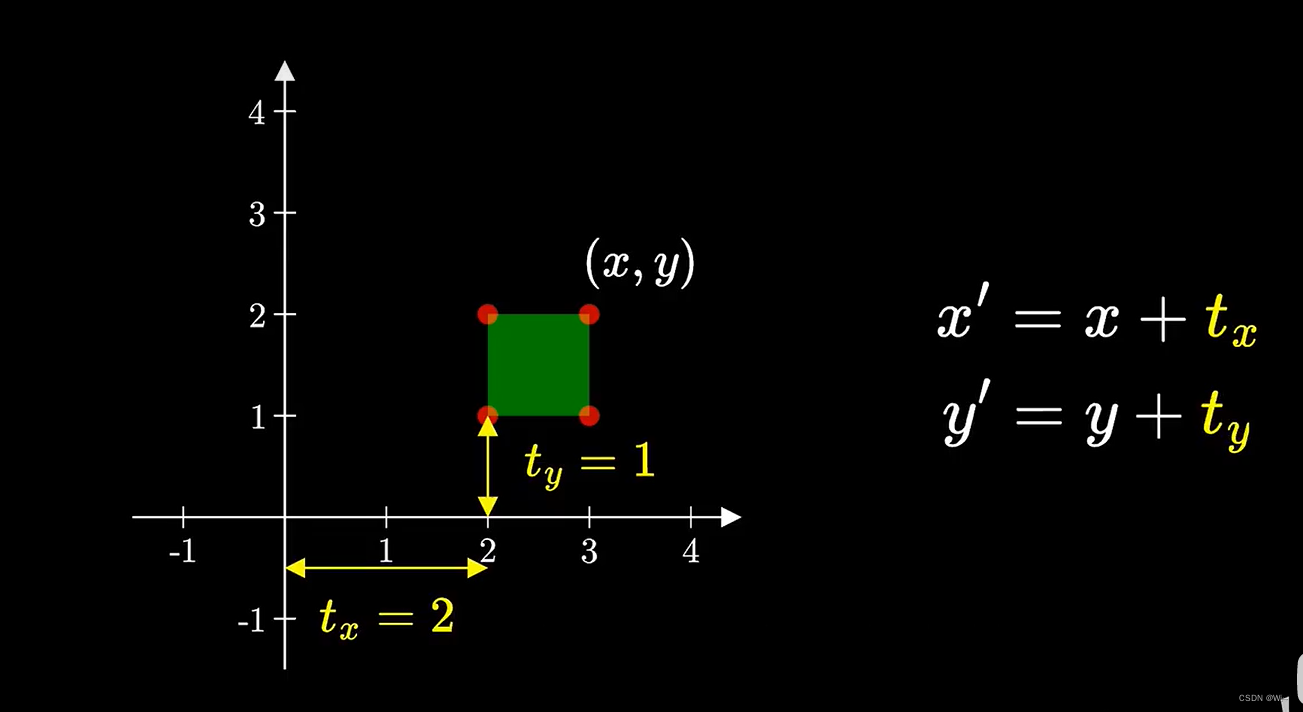
类似的,如果我们想要平移空间中的物体，假设在x方向上的位移是tx, y方向是ty，那么同理变换之后的坐标可以表示成右边的公式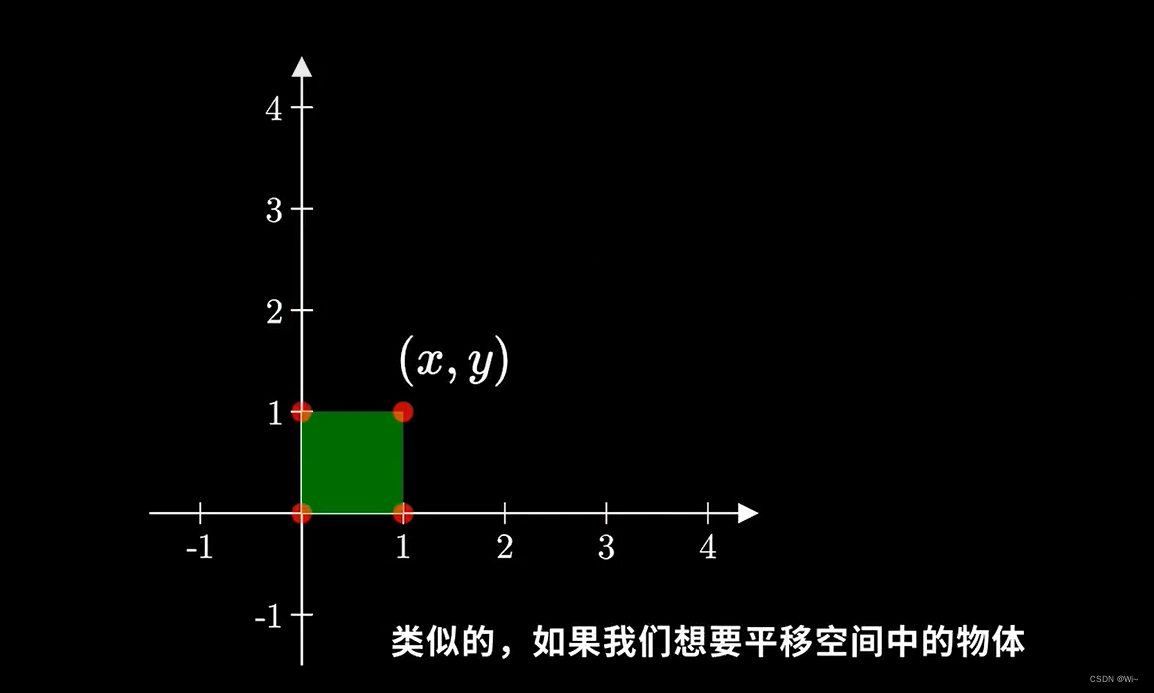
3：平移转换为齐次矩阵与其他变换相结合
由于矩阵乘法做的是对应元素相乘再相加的计算
我们并没有办法直接将平移改写成矩阵的形式
对比公式我们会发现其中缺少一个常数项
我们可以将二维坐标(x,y)通过一个三维向量来表示
并且简单地将第三维设置成1
然后再使用一个3x3的矩阵来做变换
并且将平移量写在矩阵的第三列
而它展开就刚好是我们之前讲到的平移公式
这种给向量再添加一个维度的技巧也被叫做齐次坐标
这样我们可以统一用3x3的矩阵来表示二维空间中的任意变换(平移/缩放/旋转)
相应的三维空间的变换则可以用4x4的矩阵来表示
4：旋转
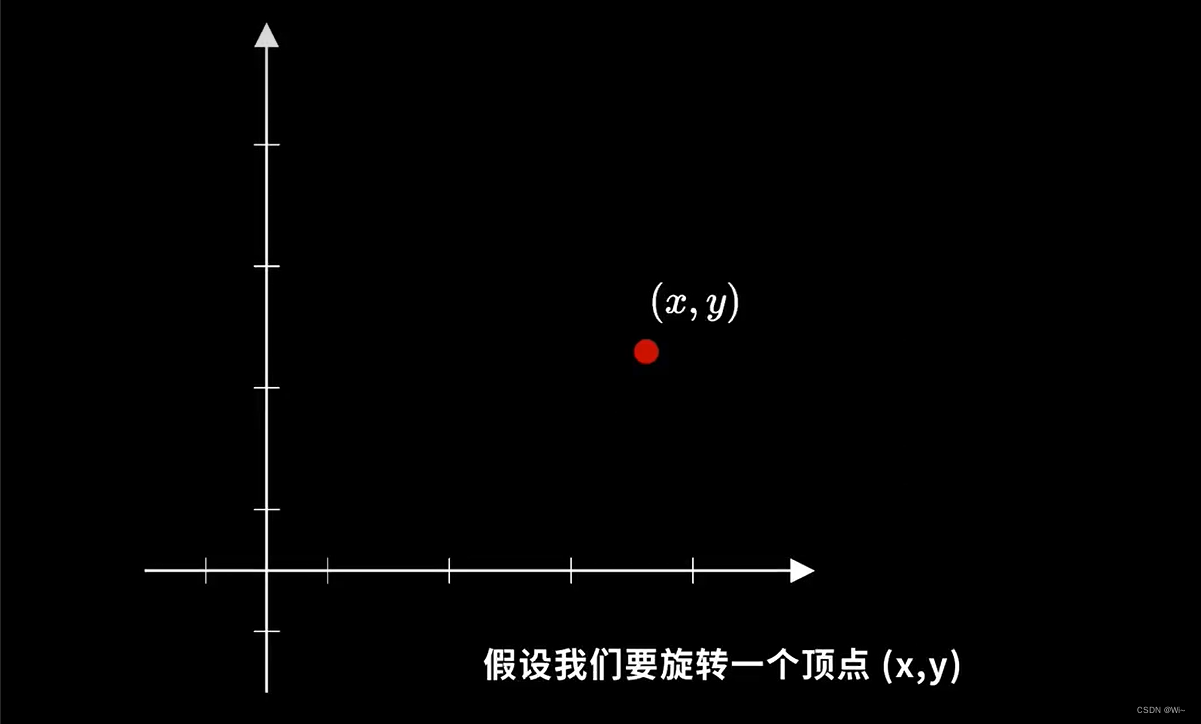
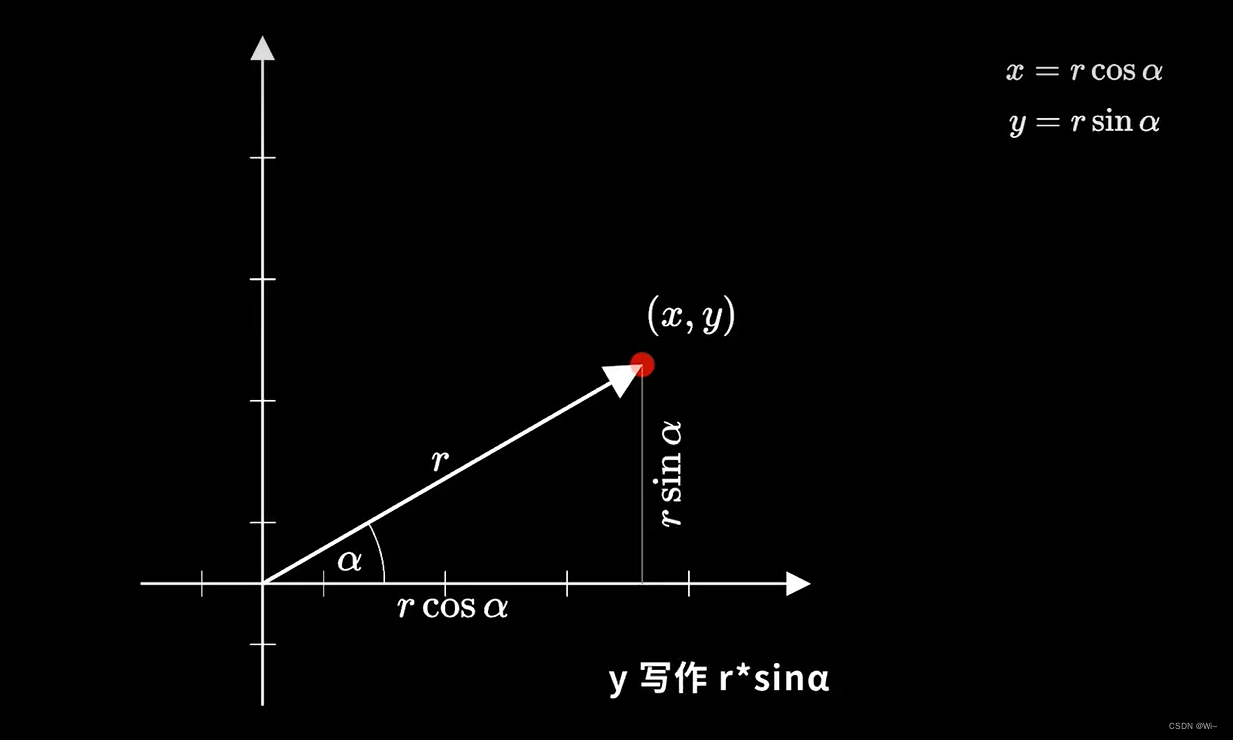
假设我们要旋转一个顶点(x,y)
它与原点的距离为r，与原点形成的夹角为α
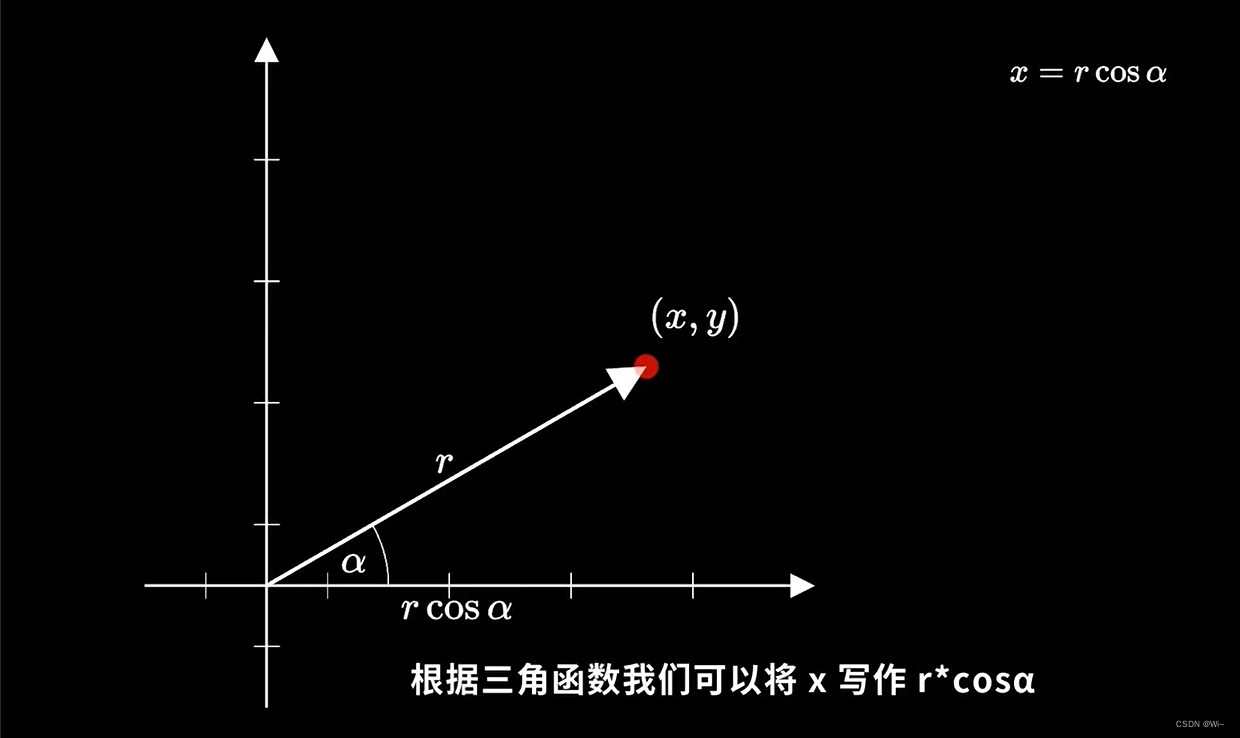
根据三角函数我们可以将x写作r * cosα，y写作r * sinα
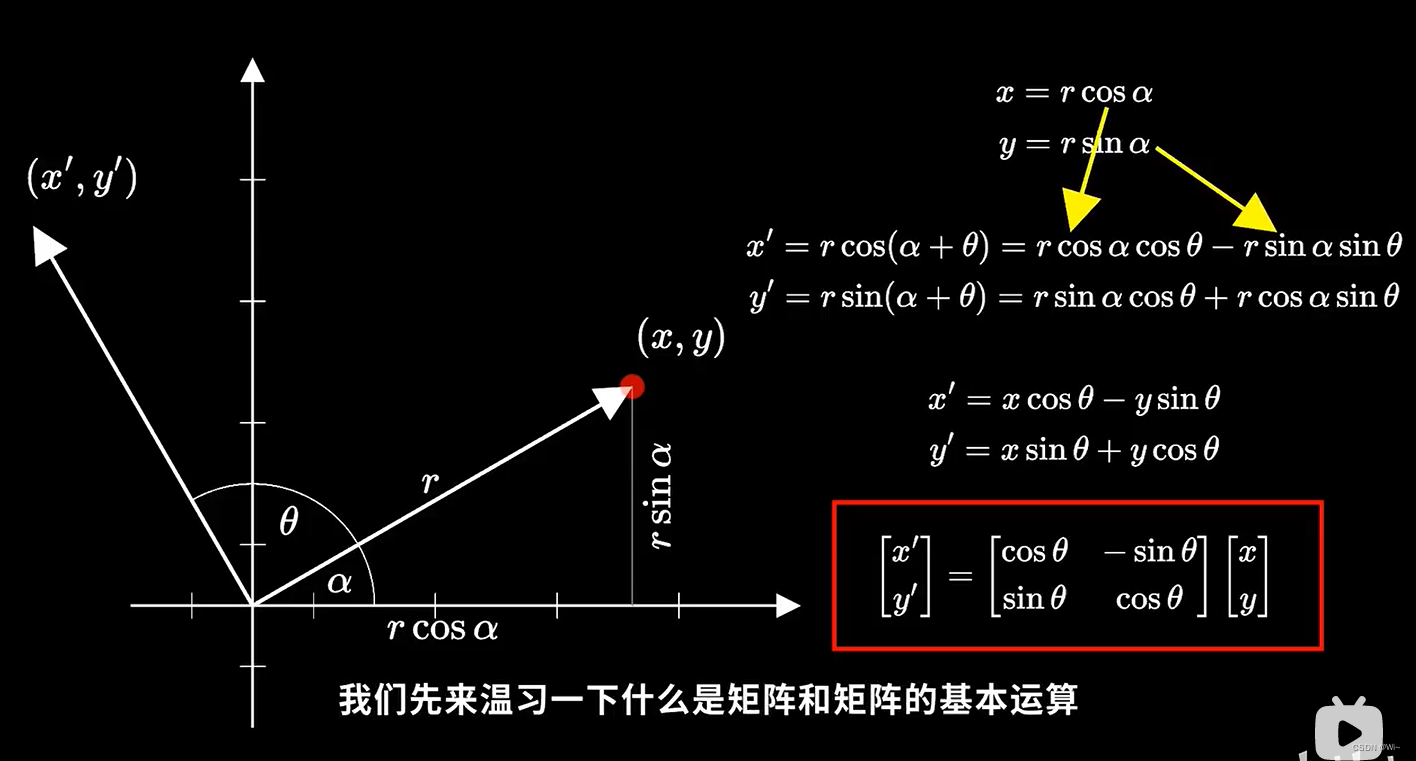
假设我们沿着原点逆时针旋转这个顶点θ角度
那么旋转后的坐标可以被类似地写作x’=cos(α+θ)，y’=sin(α+θ)
通过三角函数的加法定理
这里的cos(α+θ)可以被展开成 cosαcosθ-sinasinθ
而sin(α+θ)被展开成 sinαcosθ+cosαsinθ
最后我们带入之前的公式
可以将旋转后的坐标x’,y’表示成旋转前的坐标与三角函数的乘积之和
这个公式还可以被进一步简化成下面这种矩阵的形式
图中用到的三角函数证明链接
5：矩阵相乘具有结合性
