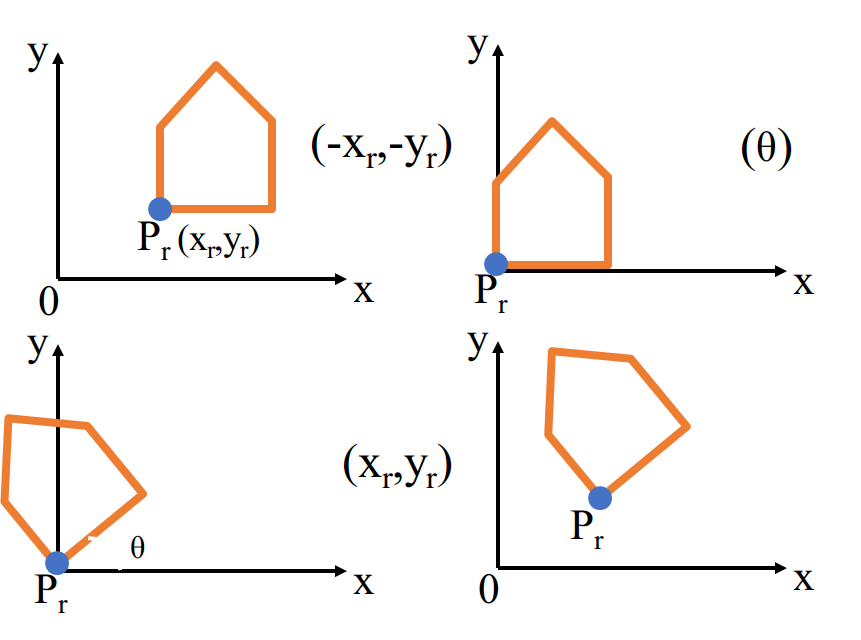一、基本变换
1. 平移
定义:将物体沿直线路径从一个坐标位置移到另一个坐标位置的重定位。不产生变形而移动物体的刚体变换。
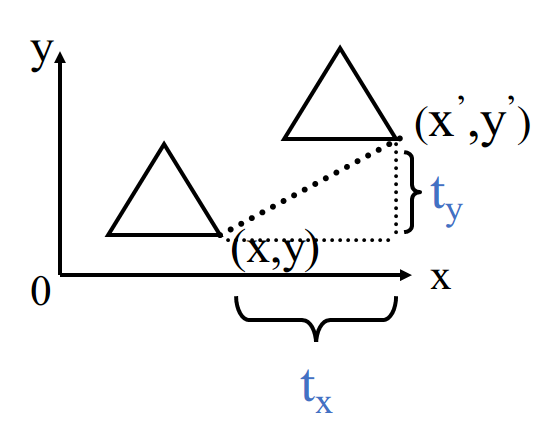
原始坐标位置:\((x,y)\),平移距离\(t_x\)、\(t_y\),新位置\((x',y')\),则\(x'=x+t_x,y'=y+t_y\)
表示为矩阵形式,令:
\[\vec{P}=\begin{pmatrix}x \\ y\end{pmatrix}\quad\vec{P'}=\begin{pmatrix}x' \\ y'\end{pmatrix}\quad\vec{T}=\begin{pmatrix}t_x \\ t_y\end{pmatrix} \]
二位平移方程:
\[\vec{P'}=\vec{P}+\vec{T} \]
2. 旋转
当参考点为\((0,0)\)
定义:以某个参考点为圆心,将对象上的各点\((x,y)\)围绕圆心转动一个逆时针角度\(θ\),变成新的坐标\((x’,y’)\)的变换。

\[x’=rcos(φ+θ)=rcosφcosθ-rsinφsinθ\\y’=rsin(φ+θ)=rsinφcosθ+rcosφsinθ\\∵x= rcosφ, y= rsinφ\\\therefore x’=xcosθ-ysinθ\quad y’=xsinθ+ycosθ \]
令:
\[\vec{R}=\begin{pmatrix}cosθ & -sinθ\\ -sinθ & cosθ\end{pmatrix} \]
写成矩阵形式:\(\vec{P'}=\vec{R}\cdot \vec{P}\)
绕任意指定的旋转位置\((x_r,y_r)\)旋转的变换方程
-
将坐标系原点平移到\((x_r,y_r)\)
-
在新的坐标系下做旋转变换
-
将坐标原点平移回原坐标系
\[x’=x_r+(x-x_r)cosθ-(y-y_r)sinθ\\y’=y_r+(x-x_r)sinθ+(y-y_r)cosθ \]
3. 变化(缩放)Scaling
定义:使对象按比例因子Sx和Sy放大或缩小的变换。
\[x’=x\cdot S_x\qquad y’=y\cdot S_y \]
令
\[\vec{S} =\begin{pmatrix}S_x & 0\\ 0 & S_y\end{pmatrix} \]
矩阵形式:\(\vec{P'} = \vec{S} \cdot \vec{P}\)
\(S_x\)、\(S_y\)均小于1,缩小物体尺寸,\(S_x\)、\(S_y\)均大于1,放大物体。\(S_x=S_y\),则保持物体相对比例缩放一致。
特殊情况
- 当\(Sy=-1\)、\(Sx=1\),按\(x\)轴反射
- 当\(Sy=1\)、\(Sx=-1\),按\(y\)轴反射
- 当\(Sy=-1\)、\(Sx=-1\),按原点\((0,0)\)反射
二、变换矩阵
每个基本变换均可表示为普通矩阵形式:
\[\vec{P’}=\vec{M_1}\vec{P}+\vec{M_2} \]
平移
将\(2\times 2\)矩阵扩充为\(3\times 3\)矩阵,将二维几何变换的乘法和平移项组合成单一矩阵表示平移。
\[\begin{pmatrix}x' \\ y' \\1\end{pmatrix}=\begin{pmatrix}1 & 0 & t_x\\ 0 & 1 & t_y\\0 & 0 & 1\end{pmatrix}\cdot\begin{pmatrix}x \\ y \\1\end{pmatrix} \]
\[\vec{P’}=\vec{T}(t_x, t_y)\vec{P} \]
绕原点的旋转
\[\begin{pmatrix}x' \\ y' \\1\end{pmatrix}=\begin{pmatrix}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\0 & 0 & 1\end{pmatrix}\cdot\begin{pmatrix}x \\ y \\1\end{pmatrix} \]
\[\vec{P’}=\vec{R}(\theta)\vec{P} \]
相对于坐标原点的缩放
\[\begin{pmatrix}x' \\ y' \\1\end{pmatrix}=\begin{pmatrix}S_x & 0 & 0\\ 0 & S_y & 0\\0 & 0 & 1\end{pmatrix}\cdot\begin{pmatrix}x \\ y \\1\end{pmatrix} \]
\[\vec{P’}=\vec{S}(S_x,S_y)\vec{P} \]
三、复合变换
1. 平移
设两个连续的平移向量\((t_{x1},t_{y1})\)和\((t_{x2},t_{y2})\)被用于坐标位置\(P\),则最后的变换位置\(P’\)。
\[\vec{P’}=\vec{T}(t_{x2},t_{y2}){\vec{T}(t_{x1},t_{y1})\vec{P}}={\vec{T}(t_{x2},t_{y2})\cdot \vec{T}(t_{x1},t_{y1})}\cdot \vec{P} \\\vec{T}(t_{x2},t_{y2})\cdot \vec{T}(t_{x1},t_{y1})=\vec{T}(t_{x1}+t_{x2},t_{y1}+t_{y2})\\\therefore \vec{P’}=\vec{T}(t_{x1}+t_{x2},t_{y1}+t_{y2})\cdot \vec{P} \\ \]
2. 旋转
\[\vec{P’}=\vec{R}(θ_2){\vec{R}(θ_1)\cdot \vec{P}}=\vec{R}(θ_2)\cdot \vec{R}(θ_1)\cdot \vec{P}\\\vec{R}(θ_2)\cdot \vec{R}(θ_1)=\vec{R}(θ_1+θ_2)\\\therefore \vec{P’}=\vec{R}(θ_2+θ_1)\cdot \vec{P} \]
3. 缩放
\[\vec{S}(S_{x2}\cdot S_{y2})\cdot \vec{S}(S_{x1}\cdot S_{y1})=\vec{S}(S_{x1}\cdot S_{x2},S_{y1}\cdot S_{y2}) \]
绕任意指定的旋转位置\((x_r,y_r)\)旋转的复合变换矩阵
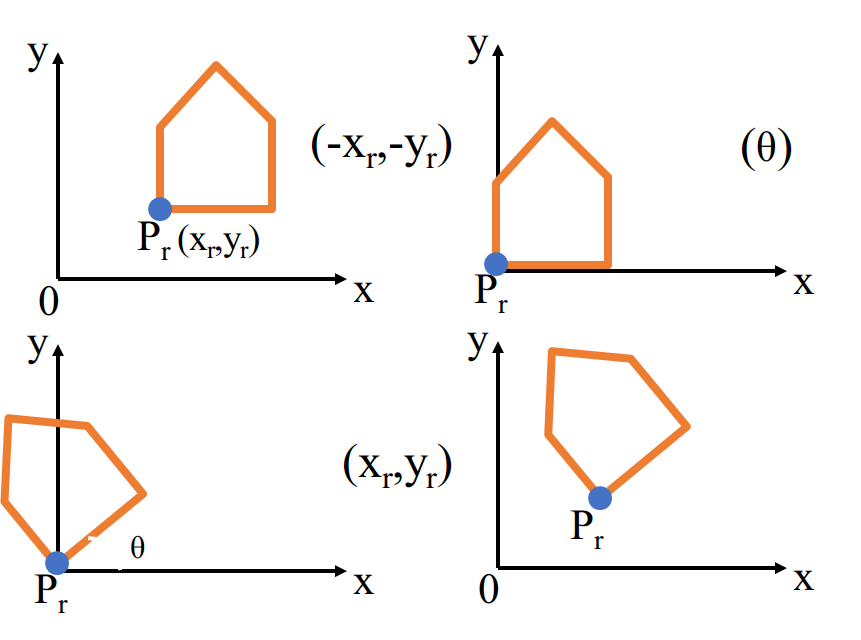
\[\begin{pmatrix}1 & 0 & x_r\\ 0 & 1 &y_r\\0 & 0 & 1\end{pmatrix}\begin{pmatrix}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\0 & 0 & 1\end{pmatrix}\begin{pmatrix}1 & 0 & -x_r\\ 0 & 1 & -y_r\\0 & 0 & 1\end{pmatrix}=\begin{pmatrix}cos\theta & -sin\theta & x_r(1-cos\theta)+y_rsin\theta\\ sin\theta & cos\theta & y_r(1-cos\theta)-x_rsin\theta\\0 & 0 & 1\end{pmatrix} \]
结论
复合操作要有效进行应先形成变换矩阵,合并所有变换序列。
四、仿射变换
形式为:
\[x'=a_{xx}x+a_{xy}y+b_x\\y'=a_{yx}x+a_{yy}y+b_y \]
的坐标变换称为二维仿射变换
\(x’,y’\)为\(x,y\)的线性函数
仿射变换具有平行线转换到平行线,有限点映射到有限点的特征。平移,旋转,缩放,反射,错切是二维仿射变换的特例。