信息熵与信息差

信息的度量[编辑]

信息熵[编辑]

美国数学家克劳德·香农被称为“信息论之父”。人们通常将香农于1948年10月发表于《贝尔系统技术学报》上的论文《通信的数学理论》作为现代信息论研究的开端。这一文章部分基于哈里·奈奎斯特和拉尔夫·哈特利于1920年代先后发表的研究成果。在该文中，香农给出了信息熵的定义：

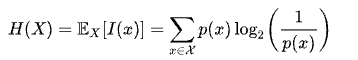
�(�)=��[�(�)]=∑�∈��(�)log2⁡(1�(�)) $H(X)=\mathbb {E} _{X}[I(x)]=\sum _{x\in {\mathcal {X}}}^{}p(x)\log _{2}\left({\frac {1}{p(x)}}\right)$

其中� ${\mathcal {X}}$ 为有限个事件x的集合，� $X$ 是定义在� ${\mathcal {X}}$ 上的随机变量。信息熵是随机事件不确定性的度量。

信息熵与物理学中的热力学熵有着紧密的联系:

�(�)=��(�) $S(X)=k_{B}H(X)$

其中S(X)为热力学熵，H(X)为信息熵，�� $k_{B}$ 为波兹曼常数。事实上这个关系也就是广义的波兹曼熵公式，或是在正则系综内的热力学熵表示式。如此可知，玻尔兹曼与吉布斯在统计物理学中对熵的工作，启发了信息论的熵。

信息熵是信源编码定理中，压缩率的下限。若编码所用的资讯量少于信息熵，则一定有资讯的损失。香农在大数定律和渐进均分性的基础上定义了典型集和典型序列。典型集是典型序列的集合。因为一个独立同分布的� $X$ 序列属于由� $X$ 定义的典型集的机率大约为1，所以只需要将属于典型集的无记忆� $X$ 信源序列编为唯一可译码，其他序列随意编码，就可以达到几乎无损失的压缩。

例子[编辑]

设有一个三个面的骰子，三面分别写有1,2,3 $1,2,3$ ，� $X$ 为掷得的数，掷得各面的概率为

�(�=1)=1/5,�(�=2)=2/5,�(�=3)=2/5, ${\begin{aligned}\mathbb {P} (X=1)&=1/5,\\\mathbb {P} (X=2)&=2/5,\\\mathbb {P} (X=3)&=2/5,\end{aligned}}$

则

�(�)=15log2⁡(5)+25log2⁡(52)+25log2⁡(52)≈1.522. $H(X)={\frac {1}{5}}\log _{2}(5)+{\frac {2}{5}}\log _{2}\left({\frac {5}{2}}\right)+{\frac {2}{5}}\log _{2}\left({\frac {5}{2}}\right)\approx 1.522.$

联合熵与条件熵[编辑]

联合熵（Joint Entropy）由熵的定义出发，计算联合分布的熵：

�(�,�)=∑�∈�∑�∈��(�,�)log⁡(1�(�,�)). $H(X,Y)=\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}^{}p(x,y)\log \left({\frac {1}{p(x,y)}}\right).$

条件熵（Conditional Entropy），顾名思义，是以条件机率�(�|�) $p(y|x)$ 计算：

�(�|�)=∑�∈�∑�∈��(�,�)log⁡(1�(�|�)). $H(Y|X)=\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}^{}p(x,y)\log \left({\frac {1}{p(y|x)}}\right).$

由贝氏定理，有�(�,�)=�(�|�)�(�) $p(x,y)=p(y|x)p(x)$ ，代入联合熵的定义，可以分离出条件熵，于是得到联合熵与条件熵的关系式:

�(�,�)=�(�)+�(�|�)=�(�)+�(�|�)=�(�,�). $H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)=H(Y,X).$

链式法则[编辑]

可以再对联合熵与条件熵的关系做推广，假设现在有� $n$ 个随机变量��,�=1,2,...,� $X_{i},i=1,2,...,n$ ，重复分离出条件熵，有：

�(�1,�2,...,��)=�(�1)+�(�2,...,��|�1)=�(�1)+�(�2|�1)+�(�3,...,��|�1,�2)=�(�1)+∑�=2��(��|�1,...,��−1). ${\begin{aligned}H(X_{1},X_{2},...,X_{n})&=H(X_{1})+H(X_{2},...,X_{n}|X_{1})\\&=H(X_{1})+H(X_{2}|X_{1})+H(X_{3},...,X_{n}|X_{1},X_{2})\\&=H(X_{1})+\sum _{i=2}^{n}H(X_{i}|X_{1},...,X_{i-1})\end{aligned}}.$

其直观意义如下：假如接收一段数列{�1,�2,...,��} $\{X_{1},X_{2},...,X_{n}\}$ ，且先收到�1 $X_1$ ，再来是�2 $X_2$ ，依此类推。那么收到�1 $X_1$ 后总讯息量为�(�1) $H(X_{1})$ ，收到�2 $X_2$ 后总讯息量为�(�1)+�(�2|�1) $H(X_{1})+H(X_{2}|X_{1})$ ，直到收到�� $X_{n}$ 后，总讯息量应为�(�1,...,��) $H(X_{1},...,X_{n})$ ，于是这个接收过程给出了链式法则。

互信息[编辑]

互信息（Mutual Information）是另一有用的信息度量，它是指两个事件集合之间的相关性。两个事件� $X$ 和� $Y$ 的互信息定义为：

�(�;�)=�(�)−�(�|�)=�(�)+�(�)−�(�,�)=�(�)−�(�|�)=�(�;�). $I(X;Y)=H(X)-H(X|Y)=H(X)+H(Y)-H(X,Y)=H(Y)-H(Y|X)=I(Y;X).$

其意义为，� $Y$ 包含� $X$ 的多少资讯。在尚未得到� $Y$ 之前，对� $X$ 的不确定性是�(�) $H(X)$ ，得到� $Y$ 后，不确定性是�(�|�) $H(X|Y)$ 。所以一旦得到� $Y$ ，就消除了�(�)−�(�|�) $H(X)-H(X|Y)$ 的不确定量，这就是� $Y$ 对� $X$ 的资讯量。