文章目录

前言
一、3D基础

前言

3D基础内容包括以下几个方面：

三维坐标系与向量：了解三维坐标系的构成以及如何在其中进行点的表示，同时需要掌握向量的定义、运算和应用。
三维几何图形：熟悉点、线、面、体等基本几何图形的定义、属性和变换，包括平移、旋转、缩放等。
三维建模：掌握基本的三维建模技巧，包括建模软件的使用、多边形建模、曲线建模、NURBS等。
光照和材质：了解光照的基本概念、类型以及如何应用到三维场景中，同时需要掌握材质的定义和属性。
动画和渲染：掌握三维动画的基本原理和制作方法，了解渲染技术的基础知识。
三维游戏开发相关：了解三维游戏开发的基础和流程，掌握游戏引擎的使用以及基础的编程技能（如C++和OpenGL ES）。

以上这些知识点是3D基础内容中比较重要的部分，如果想要深入学习3D相关的知识，还需要进一步了解数学、物理和计算机图形学等相关学科。

一、3D基础

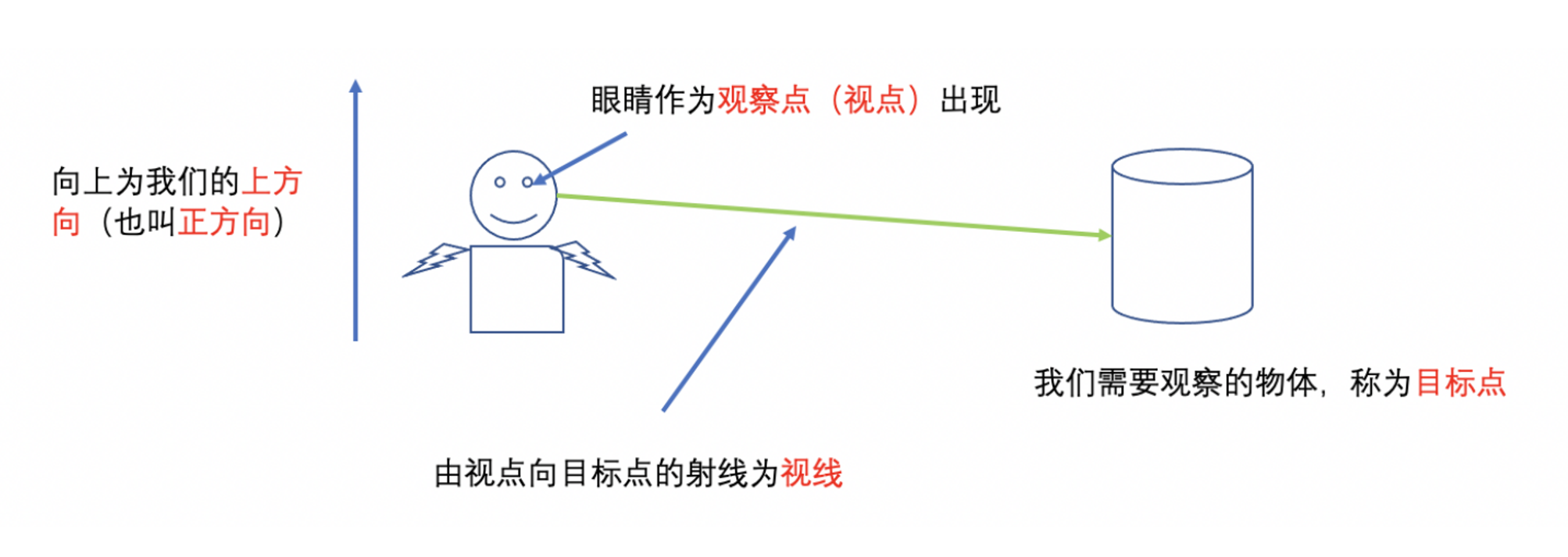
1. 视点、目标点、上方向

在3D基础中，视点、目标点和上方向是非常重要的概念，它们用于确定3D场景的视角和方向。

视点（Eye Point）：视点指的是观察者所在的位置，也可以称为摄像机位置。视点决定了观察者在场景中的位置和角度，从视点的位置观察场景可以得到不同的视角和效果。
目标点（Target Point）：目标点指的是观察者所看的物体位置，或者说是观察者所关注的点。目标点决定了观察者的注视方向和目标物体在视野中的位置。
上方向（Up Vector）：上方向指的是视点相对于场景中的上方向，也可以说是摄像机的顶部朝向。上方向决定了场景中的物体与视野的相对位置关系，比如一个物体在视图中的上方、下方、左侧或右侧等。

这些概念通常都是以向量的形式来表示的，视点和目标点可以表示为三维坐标系中的两个点，而上方向则表示为一个向量。在计算机图形学中，这些概念通常用于计算观察矩阵和投影矩阵，从而实现3D场景的渲染和动画效果。

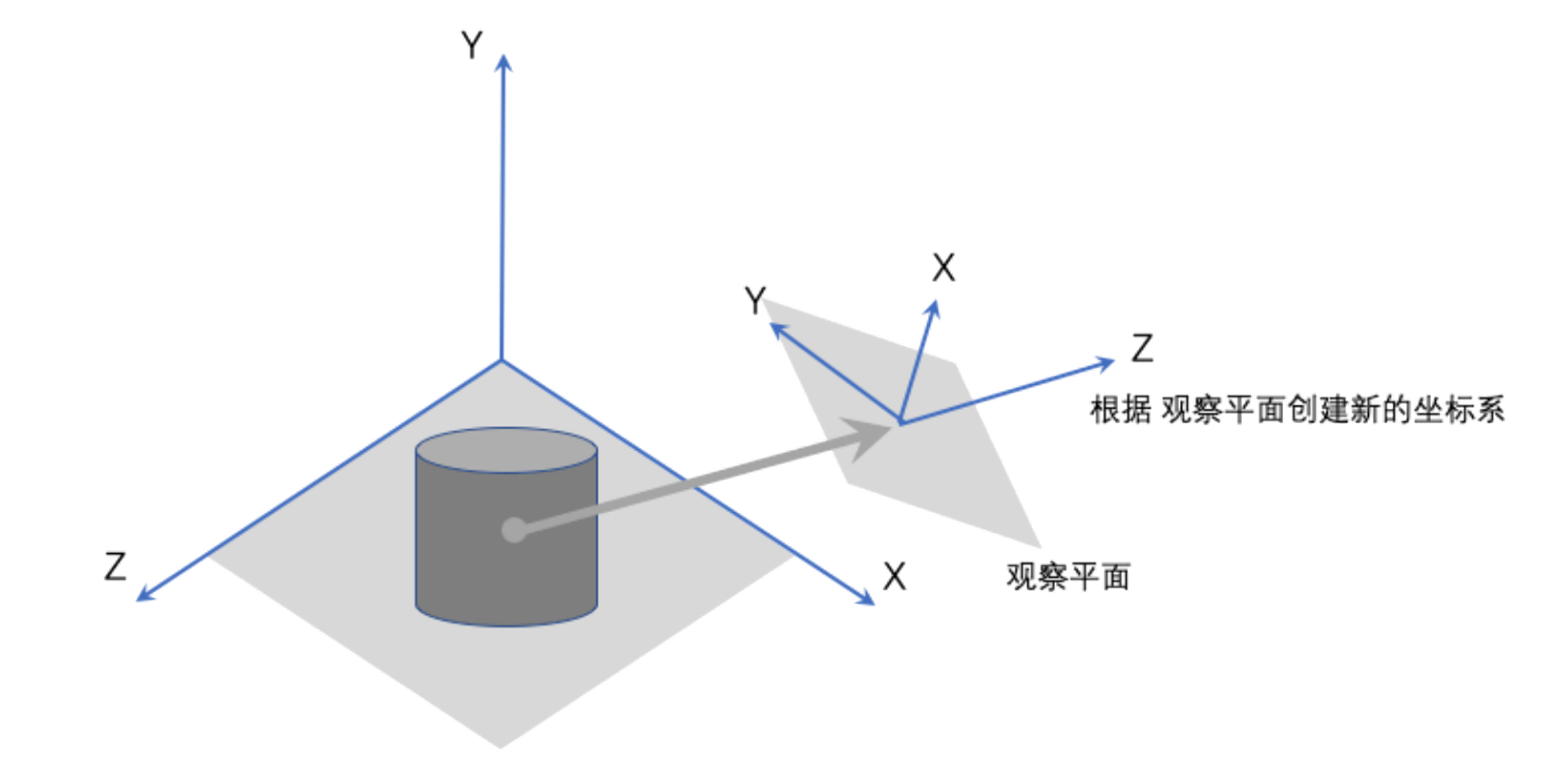
在这里插入图片描述

2. 观察平面

3D基础的观察平面是指在三维坐标系中，我们所观察的物体在一个平面上显示的方式。这个平面通常被称为投影平面或视口（Viewport）。视口是一个矩形区域，它定义了我们所能看到的区域，并将三维场景中的物体映射到二维平面上。

在3D计算机图形学中，观察平面是指我们选择的一个视角，通过这个视角观察场景，并将其映射到视口上。观察平面通常与视口平面平行，因此将视口平面定义为观察平面。

不同的观察平面会导致对象的不同投影效果，例如平行投影和透视投影。平行投影是指在观察平面上，物体投影呈现为等比例的二维图形。而透视投影则是模仿人眼观察物体时的效果，使得远离观察平面的物体看起来比近处的物体更小。

因此，在进行3D图形的渲染时，我们需要选择合适的观察平面以及投影方式，以最大程度地展现出所需效果。
在这里插入图片描述

<!DOCTYPE html>
<html lang="en">
<head>
  <meta charset="UTF-8">
  <title>Title</title>
  <script src="../lib/index.js"></script>
  <style>
    * {
    
    
      margin: 0;
      padding: 0;
    }

    canvas{
    
    
      margin: 50px auto 0;
      display: block;
      background: yellow;
    }
  </style>
</head>
<body>
<canvas id="canvas" width="400" height="400">
  此浏览器不支持canvas
</canvas>
</body>
</html>
<script>
  // 视图矩阵获取
  function getViewMatrix(eyex, eyey, eyez, lookAtx, lookAty, lookAtz, upx, upy, upz) {
    
    

    // 视点
    const eye = new Float32Array([eyex, eyey, eyez])

    // 目标点
    const lookAt = new Float32Array([lookAtx, lookAty, lookAtz])
    
    // 上方向
    const up = new Float32Array([upx, upy, upz])

    // 确定z轴
    const z = minus(eye, lookAt);

    normalized(z);
    normalized(up);

    // 确定x轴
    const x = cross(z, up);

    normalized(x);
    // 确定y轴
    const y = cross(x, z);

    return new Float32Array([
      x[0],       y[0],       z[0],       0,
      x[1],       y[1],       z[1],       0,
      x[2],       y[2],       z[2],       0,
      -dot(x,eye),-dot(y,eye),-dot(z,eye),1
    ])
  }
  const ctx = document.getElementById('canvas')

  const gl = ctx.getContext('webgl')

  // 创建着色器源码
  const VERTEX_SHADER_SOURCE = `
    attribute vec4 aPosition;
    uniform mat4 mat;
    void main() {
      gl_Position = mat * aPosition;
      gl_PointSize = 10.0;
    }
  `; // 顶点着色器

  const FRAGMENT_SHADER_SOURCE = `
    void main() {
      gl_FragColor = vec4(1.0,0.0,0.0,1.0);
    }
  `; // 片元着色器

  const program = initShader(gl, VERTEX_SHADER_SOURCE, FRAGMENT_SHADER_SOURCE)

  const aPosition = gl.getAttribLocation(program, 'aPosition');
  const mat = gl.getUniformLocation(program, 'mat');

  const points = new Float32Array([
    -0.5, -0.5,
    0.5, -0.5,
    0.0,  0.5,
  ])

  const buffer = gl.createBuffer();

  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);

  gl.bufferData(gl.ARRAY_BUFFER, points, gl.STATIC_DRAW);

  gl.vertexAttribPointer(aPosition, 2, gl.FLOAT, false, 0, 0);

  gl.enableVertexAttribArray(aPosition)

  let eyey = -0.1;
  function animation() {
    
    
    eyey += 0.01;
    if (eyey > 1) {
    
    
      eyey = -0.1;
    }

    const vm = getViewMatrix(0.0,eyey,0.2,0.0,0.0,0.0,0.0,0.6,0.0);
    // const matrix = getTranslateMatrix(x, x);
    // gl.vertexAttrib1f(aTranslate, x);
    gl.uniformMatrix4fv(mat, false, vm);
    gl.drawArrays(gl.TRIANGLES, 0, 3);

    requestAnimationFrame(animation);
  }

  animation()
</script>

在这里插入图片描述

3. 辅助函数

3.1 归一化函数

归一化函数是一种将数据缩放到特定范围内的函数，常常用于数据预处理和特征缩放中。通常，归一化函数将原始数据映射到0到1之间的范围内，使得数据具有相同的尺度和范围，以便更好地进行比较和分析。

常见的归一化函数有最小-最大缩放法（Min-Max Scaling）、Z-score归一化法、小数定标规范化法等。其中，最小-最大缩放法是将原始数据中的最小值缩放到0，最大值缩放到1，其他值按比例缩放到0和1之间。Z-score归一化法是将原始数据的均值缩放到0，标准差缩放到1，使得数据分布近似于标准正态分布。小数定标规范化法是将原始数据除以某个基数的幂次方，使得缩放后的数据的最大绝对值不超过1。

归一化函数的具体选择取决于数据特点和应用需求。

在WebGL中，归一化函数的作用是将给定的坐标或向量转换为标准化设备坐标系中的坐标或向量。标准化设备坐标系是一个正方形区域，其范围从(-1, -1, -1)到(1, 1, 1)，其中x、y和z坐标都在-1到1之间。归一化函数将给定的坐标或向量除以其长度或某个常数，以保证其值在标准化设备坐标系中的范围内。这是为了让WebGL引擎能够正确渲染三维场景，因为WebGL引擎只能处理在标准化设备坐标系中的坐标或向量。

// 归一化函数
function normalized(arr) {
    
    
  let sum = 0;

  for (let i = 0; i < arr.length; i++) {
    
    
    sum += arr[i] * arr[i]
  }

  const middle = Math.sqrt(sum);

  for (let i = 0; i < arr.length; i++) {
    
    
    arr[i] = arr[i] / middle;
  }
}

3.2 叉积

叉积是向量运算中的一种，表示两个向量相乘的结果是一个垂直于这两个向量的向量。具体来说，如果有两个向量 $\vec{a}$ 和 $\vec{b}$ ，则它们的叉积 $\vec{c}=\vec{a}\times \vec{b}$ 的结果为：

$\vec{c}$ 的方向垂直于 $\vec{a}$ 和 $\vec{b}$ 所在的平面；
$\vec{c}$ 的模长等于以 $\vec{a}$ 和 $\vec{b}$ 所在平面为底面的平行四边形的面积；
$\vec{a}$ 、 $\vec{b}$ 和 $\vec{c}$ 满足右手定则。

因此，叉积的作用有：

计算平面上向量的垂直向量。在计算空间中的向量积时，可以用三维向量 $\vec{i}$ 、 $\vec{j}$ 、 $\vec{k}$ 分别表示笛卡尔坐标系的三个方向，将 $\vec{a}$ 和 $\vec{b}$ 写成分别以 $\vec{i}$ 、 $\vec{j}$ 、 $\vec{k}$ 为基的线性组合，即 $\vec{a}=a_1\vec{i}+a_2\vec{j}+a_3\vec{k}$ ， $\vec{b}=b_1\vec{i}+b_2\vec{j}+b_3\vec{k}$ ，然后按照叉积的公式计算即可。
计算平行四边形的面积。由于叉积的模长等于以 $\vec{a}$ 和 $\vec{b}$ 所在平面为底面的平行四边形的面积，因此可以利用叉积来计算平行四边形的面积。
定义旋转轴和角度。对于两个向量 $\vec{a}$ 和 $\vec{b}$ ，它们的方向已经确定了，因此它们的叉积 $\vec{c}$ 代表的向量也是确定的。这个向量可以被认为是旋转轴，而 $\vec{a}$ 和 $\vec{b}$ 的夹角 $\theta$ 可以被认为是旋转的角度。在计算机图形学中，经常使用叉积来进行物体的旋转和变换。

WebGL中的叉积函数，即cross函数，可以用于计算两个三维向量的叉积。叉积是一个向量，其方向垂直于两个向量所在的平面，大小等于这两个向量所在平面的面积。在三维图形编程中，叉积函数的应用场景很多，例如：

计算表面法向量：在计算三维物体表面的光照效果时，需要知道每个表面的法向量。可以使用cross函数计算出两个表面上的向量，然后取叉积得到该表面的法向量。
计算切线和副切线：在贴图映射中，需要计算表面的切线和副切线，以便正确地显示纹理。可以使用cross函数计算出两个切向量，以及它们的叉积得到表面的法向量，再用法向量来计算出副切线。
计算旋转轴和旋转角度：在三维图形的旋转中，需要计算旋转轴和旋转角度。可以使用cross函数计算出两个向量的叉积，来得到旋转轴。

// 叉积函数 获取法向量
function cross(a,b) {
    
    
  return new Float32Array([
    a[1] * b[2] - a[2] * b[1],
    a[2] * b[0] - a[0] * b[2],
    a[0] * b[1] - a[1] * b[0],
  ])
}

3.3 点积

点积，又称内积或数量积，是数学中两个向量之间的一种运算，用符号“·”表示。具体地，设两个n维向量a和b，它们的点积定义为：

a·b = a1b1 + a2b2 + … + anbn

也就是将两个向量对应位置的元素相乘，并将乘积相加得到的一个标量。点积在向量和矩阵运算中具有重要作用。

点积有以下几个作用：

计算向量的模长（长度）：a·a = ||a||^2，其中||a||表示向量a的长度。
判断向量的正交性和夹角：如果a·b=0，则向量a和b垂直（正交）；如果a·b>0，则向量a和b夹角小于90度，如果a·b<0，则向量a和b夹角大于90度。
求向量之间的投影：向量a在向量b上的投影长度为：（a·b）/||b||。
求夹角余弦：cosθ=(a·b)/(||a|| ||b||)。
判断向量的方向：如果a·b>0，则向量a和b同向；如果a·b<0，则向量a和b反向。
用于解线性方程组、计算矩阵的行列式，以及计算向量的夹角等。

在WebGL中，点积函数用于计算两个向量的点积（也称为内积或数量积），其结果是一个标量值。点积函数可以用于许多不同的应用中，例如：

计算两个向量之间的夹角：点积函数可以计算两个向量的夹角余弦值，从而可以确定它们之间的夹角。
投影：使用点积函数可以将一个向量投影到另一个向量上，从而得到一个在另一个向量上的向量分量。
碰撞检测：通过计算两个物体的朝向向量和相对位置向量之间的点积，可以确定它们是否相互接触或相交。
阴影计算：使用点积函数可以计算物体表面法线和光源向量之间的点积，从而确定光照强度和阴影的位置。

总之，点积函数在WebGL中具有广泛的应用，是计算向量间关系和位置的重要工具。

// 点积函数 获取投影长度
function dot(a, b) {
    
    
  return a[0] * b[0] + a[1] * b[1] + a[2] * b[2]
}

3.4 向量差

向量差是指两个向量相减得到的新向量。具体地，如果有向量A和向量B，则向量差C=A-B，表示从B指向A的向量。

向量差的作用包括：

用于求解向量间的相对位置和方向，如空间中物体的运动轨迹。
用于求解向量间的夹角和距离，如计算两点间的距离。
用于计算向量的投影和正交分解。
用于求解向量组的线性相关关系和线性方程组的解。

在WebGL中，向量差函数可以计算两个向量之间的差值。这通常用于计算两个点之间的距离或计算一个向量的方向和另一个向量的反向。向量差函数也可以用于执行几何变换，例如将物体沿某个方向移动或旋转。在WebGL中，向量差函数通常是内置的，并使用GLSL编程语言的函数库进行实现。

// 向量差
function minus(a, b) {
    
    
  return new Float32Array([
    a[0] - b[0],
    a[1] - b[1],
    a[2] - b[2],
  ])
}

【愚公系列】2023年08月 WEBGL专题-3D基础