【愚公系列】2023年08月 3D数学-矩阵运算和变换

---

前言

1.矩阵的定义

矩阵是由数字或符号排成的矩形阵列。矩阵中的每个数字或符号称为元素。矩阵用于在数学、物理学、工程学和计算机科学等领域中描述和解决线性方程组、向量、转换、空间几何等问题。矩阵通常由方括号表示，如下所示：

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]$$

其中，$a_{ij}$ 表示矩阵 $A$ 的第 $i$ 行第 $j$ 列的元素。$m$ 表示矩阵的行数，$n$ 表示矩阵的列数。如果一个矩阵的行数和列数相等，那么它就是一个方阵。

2.矩阵和方程的关系

矩阵和方程有着密切的关系，矩阵可以用来表示方程的系数，从而可以通过矩阵运算来求解方程。

具体来说，对于一个包含$n$个未知数的线性方程组，可以将其表示为如下形式：

$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2\\ \cdots \\ a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n=b_n\end{array}$$

其中，$a_{ij}$表示第$i$个方程中第$j$个未知数的系数，$b_i$表示第$i$个方程的等式右边的常数。

将上述方程组中的系数和常数放在一个$n\times (n+1)$的矩阵中，即：

$$\left(\begin{array}{ccccc}{a}_{11}& a_{12}& \cdots & a_{1n}& b_1\\ a_{21}& a_{22}& \cdots & a_{2n}& b_2\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n1}& a_{n2}& \cdots & a_{nn}& b_n\end{array}\right)$$

可以发现，在这个矩阵中，每个方程的系数和常数都被组织为矩阵的一行，而整个方程组则被组织为矩阵的$n$行。这个矩阵被称为增广矩阵。

对于这个增广矩阵，可以通过一系列矩阵变换来将其化简为一个简单的形式，从而可以求解这个方程组。

矩阵变换的具体步骤包括交换矩阵中的两行、将矩阵中某一行乘以一个非零常数、将矩阵中某一行加上另一行的某个倍数。通过这些矩阵变换，可以将增广矩阵化为如下形式：

$$\left(\begin{array}{ccccc}{a}_{11}^{{}^{\prime }}& a_{12}^{{}^{\prime }}& \cdots & a_{1n}^{{}^{\prime }}& b_1^{{}^{\prime }}\\ 0& a_{22}^{{}^{\prime }}& \cdots & a_{2n}^{{}^{\prime }}& b_2^{{}^{\prime }}\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& \cdots & a_{nn}^{{}^{\prime }}& b_n^{{}^{\prime }}\end{array}\right)$$

其中，矩阵中的斜线上方都是$0$，而斜线上的元素则称为主元。

通过这种化简方式，可以用简单的代数运算来解决方程组问题，矩阵成为了一个重要的工具。

一、矩阵运算和变换

1.矩阵运算

1.1 矩阵加减

矩阵加减是指两个相同维数的矩阵进行加减运算。

设A和B为两个n行m列的矩阵，则它们的和C = A + B也是一个n行m列的矩阵，其中C的每个元素为A和B对应元素的和，即Cij = Aij + Bij。

同理，它们的差D = A - B也是一个n行m列的矩阵，其中D的每个元素为A和B对应元素的差，即Dij = Aij - Bij。

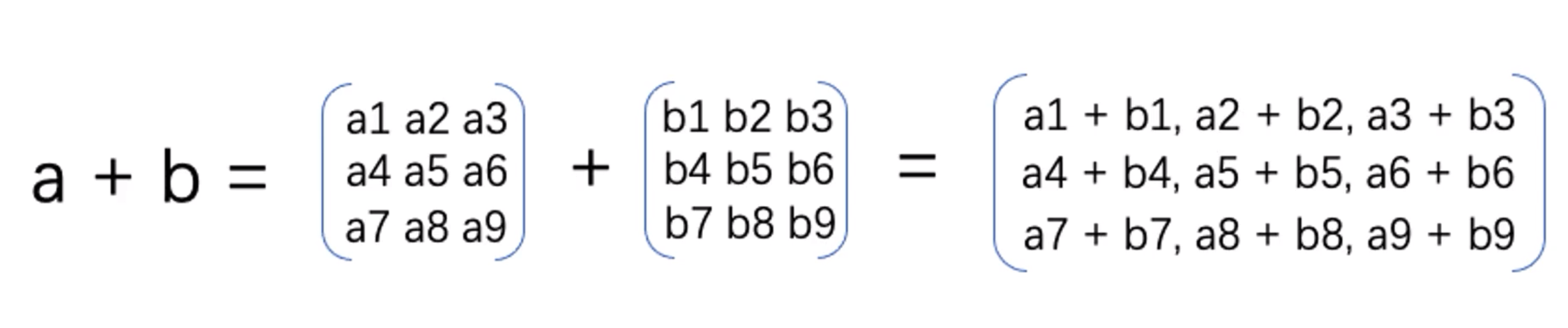
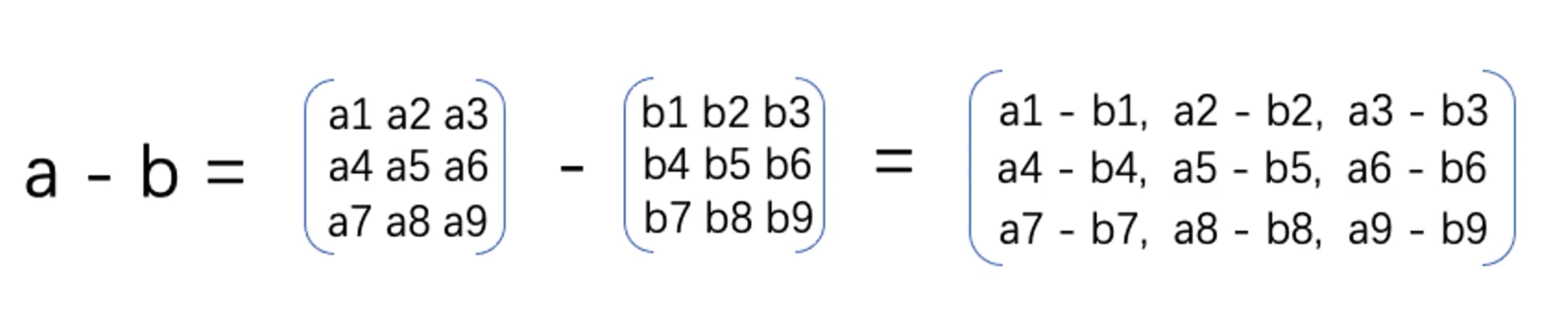
1.2 矩阵乘标量

矩阵乘标量是指将一个标量（通常为实数或复数）乘以一个矩阵的每一个元素。假设$A$是一个$m\times n$的矩阵，$k$是一个标量，则$A$乘以$k$的结果为：

$$kA=\left[\begin{array}{cccc}k{a}_{11}& k{a}_{12}& \cdots & k{a}_{1n}\\ k{a}_{21}& k{a}_{22}& \cdots & k{a}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ k{a}_{m1}& k{a}_{m2}& \cdots & k{a}_{mn}\end{array}\right]$$

其中$a_{ij}$表示矩阵$A$的第$i$行第$j$列的元素。注意，矩阵乘标量仅仅是将矩阵的每个元素乘以标量，而不会改变矩阵的形状。

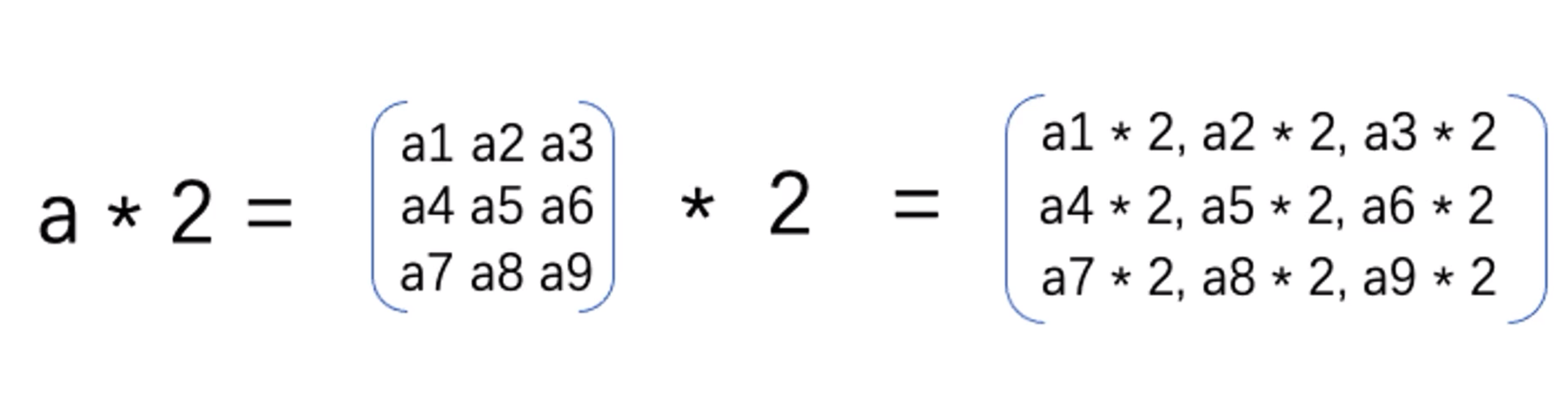
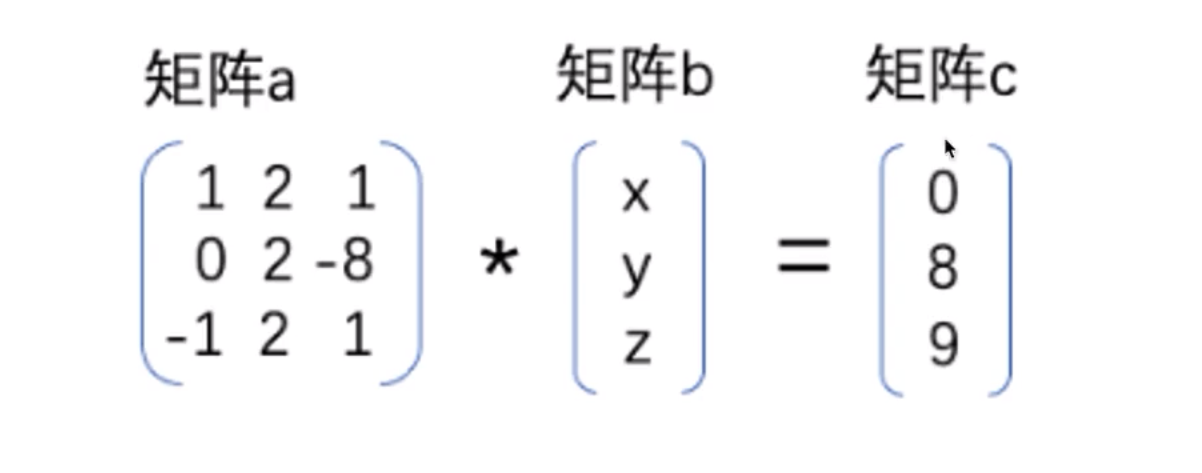
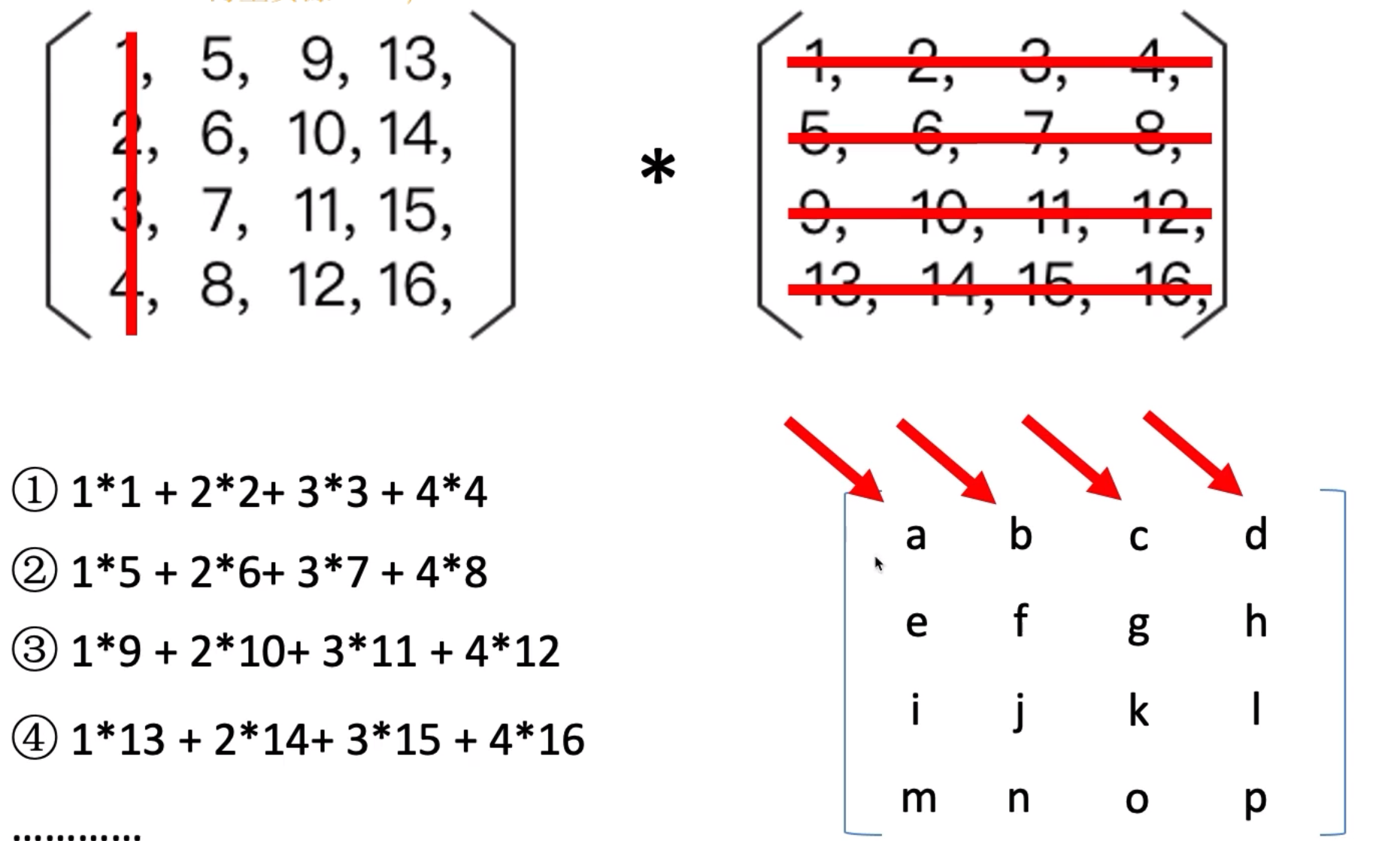
1.3 矩阵相乘

矩阵相乘是指将两个矩阵按照一定的规则进行相乘，得到一个新的矩阵。具体的规则是：

设A是一个m × n的矩阵，B是一个n × p的矩阵，那么矩阵C = AB就是一个m × p的矩阵，且它的每个元素cij都是由A的第i行与B的第j列对应元素相乘后求和得到的，即：

cij = Σ(ai * bj)，其中i = 1, 2, …, m，j = 1, 2, …, p。

其中，ai表示A矩阵第i行的元素，bj表示B矩阵第j列的元素。

需要注意的是，只有当矩阵A的列数等于矩阵B的行数时，才能进行矩阵相乘操作。否则会出现维度不匹配的错误。

2.3*3矩阵旋转

2.1 矩阵X旋转

矩阵绕X轴旋转的公式如下：

[1     0           0       ]
[0     cosθ        -sinθ   ]
[0     sinθ        cosθ    ]

其中，θ表示旋转角度。这个公式的推导可以通过以下步骤进行：

1. 假设有一个三维向量a = [x, y, z]，它绕X轴旋转θ角度后变为b = [x’, y’, z’]。

2. 我们可以将向量a投影到XOY平面上，得到长度为r = sqrt(y^2 + z^2)的向量c = [0, y/r, z/r]，即c的长度为1。

3. 根据三角函数的定义，可以得到绕X轴旋转θ角度后的向量b的坐标为：

x' = x
y' = c[2] * cosθ - c[3] * sinθ = y * cosθ - z * sinθ
z' = c[2] * sinθ + c[3] * cosθ = y * sinθ + z * cosθ

其中，c[2]表示向量c在Y轴上的投影，c[3]表示向量c在Z轴上的投影。

4. 将上面的公式写成矩阵形式，可以得到绕X轴旋转θ角度的矩阵为：

[1     0           0       ]
[0     cosθ        -sinθ   ]
[0     sinθ        cosθ    ]

这就是绕X轴旋转θ角度的矩阵公式。

2.2 矩阵Y旋转

矩阵绕Y轴旋转的角度为θ时，可以通过以下推导得出旋转矩阵：

假设需要旋转的点为P=(x, y, z)，则旋转后得到的点P’=(x’, y’, z’)，其中：

x’ = x * cosθ + z * sinθ
y’ = y
z’ = -x * sinθ + z * cosθ

将上述式子整合成矩阵形式，得到旋转矩阵R：

R = | cosθ 0 sinθ 0 |
| 0 1 0 0 |
| -sinθ 0 cosθ 0 |
| 0 0 0 1 |

其中，第一行和第三行代表了x和z坐标的旋转，第二行代表y坐标不变，最后一行代表不变量。

因此，对于任意一个绕Y轴旋转角度为θ的点P，可以通过R矩阵的变换得到旋转后的点P’。

2.3 矩阵Z旋转

假设旋转矩阵为$R_z(\theta )$，表示绕Z轴旋转角度$\theta$，则：

$$R_z(\theta )=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$

在推导过程中，我们可以使用以下两条性质：

1. 矩阵乘法结合律：$(AB)C=A(BC)$；

2. 对于任意向量$\mathbf{v}=(x,y,z{)}^T$，绕Z轴旋转角度$\theta$的公式为：

   $$\begin{array}{rl}{R}_z(\theta )\mathbf{v}& =\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]\\ & =\left[\begin{array}{c}\cos \theta x-\sin \theta y\\ \sin \theta x+\cos \theta y\\ z\end{array}\right]\end{array}$$

现在考虑将矩阵$R_z(\theta )$表示成两个矩阵的乘积的形式。我们需要将其矩阵元分解成两个矩阵的矩阵元的乘积。

设有矩阵$A$和$B$，满足：

$$AB=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]\left[\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{22}& b_{23}\\ b_{31}& b_{32}& b_{33}\end{array}\right]=\left[\begin{array}{ccc}{c}_{11}& c_{12}& c_{13}\\ c_{21}& c_{22}& c_{23}\\ c_{31}& c_{32}& c_{33}\end{array}\right]$$

则有：

$$\begin{array}{rl}{c}_{11}& =a_{11}{b}_{11}+a_{12}{b}_{21}+a_{13}{b}_{31}\\ c_{12}& =a_{11}{b}_{12}+a_{12}{b}_{22}+a_{13}{b}_{32}\\ c_{13}& =a_{11}{b}_{13}+a_{12}{b}_{23}+a_{13}{b}_{33}\\ c_{21}& =a_{21}{b}_{11}+a_{22}{b}_{21}+a_{23}{b}_{31}\\ c_{22}& =a_{21}{b}_{12}+a_{22}{b}_{22}+a_{23}{b}_{32}\\ c_{23}& =a_{21}{b}_{13}+a_{22}{b}_{23}+a_{23}{b}_{33}\\ c_{31}& =a_{31}{b}_{11}+a_{32}{b}_{21}+a_{33}{b}_{31}\\ c_{32}& =a_{31}{b}_{12}+a_{32}{b}_{22}+a_{33}{b}_{32}\\ c_{33}& =a_{31}{b}_{13}+a_{32}{b}_{23}+a_{33}{b}_{33}\end{array}$$

现在我们考虑将$R_z(\theta )$分解成两个矩阵$A$和$B$的乘积形式。注意到对于$\theta =0$时，$R_z(\theta )$就是单位矩阵，因此我们可以选择$A$和$B$满足$A=\mathbf{I}$（单位矩阵）和$B=R_z(\theta )$。

现在我们要找到矩阵$A$和$B$的矩阵元分解形式，使得$AB=R_z(\theta )$。根据矩阵乘法结合律，我们可以先假设$A$和$B$的某些矩阵元的乘积等于$R_z(\theta )$的对应矩阵元，然后求解这些矩阵元的值。

具体来说，我们假设：

$$\begin{array}{rlrlr}{a}_{11}{b}_{11}+a_{12}{b}_{21}+a_{13}{b}_{31}& =\cos \theta & & a_{11}{b}_{12}+a_{12}{b}_{22}+a_{13}{b}_{32}& =-\sin \theta \\ a_{21}{b}_{11}+a_{22}{b}_{21}+a_{23}{b}_{31}& =\sin \theta & & a_{21}{b}_{12}+a_{22}{b}_{22}+a_{23}{b}_{32}& =\cos \theta \\ a_{31}{b}_{11}+a_{32}{b}_{21}+a_{33}{b}_{31}& =0& & a_{31}{b}_{12}+a_{32}{b}_{22}+a_{33}{b}_{32}& =0\end{array}$$

由此可以得到：

$$A=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right],B=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

因此，我们可以将$R_z(\theta )$表示成两个矩阵的乘积形式：

$$R_z(\theta )=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

这就是$R_z(\theta )$的矩阵分解形式，其中第一个矩阵表示绕Z轴旋转$\theta$角度的变换，第二个矩阵表示单位变换。

3.4*4矩阵旋转

3.1 矩阵X旋转

首先，我们需要知道绕X轴旋转的矩阵表达式：

$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$

其中，$\theta$表示绕X轴旋转的角度。

接下来，我们来推导4*4矩阵绕X旋转矩阵。

假设我们有一个4*4矩阵A：

$\left[\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& a_{34}\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right]$

为了让矩阵A绕X轴旋转，我们可以如下操作：

1. 将矩阵A进行平移，使其中心点处于原点。

这一步操作可以通过平移矩阵来实现：

$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ -\frac{a_{11}+a_{21}+a_{31}+a_{41}}{4}& -\frac{a_{12}+a_{22}+a_{32}+a_{42}}{4}& -\frac{a_{13}+a_{23}+a_{33}+a_{43}}{4}& 1\end{array}\right]\left[\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& a_{34}\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right]=\left[\begin{array}{cccc}{a}_{11}^{\prime }& a_{12}^{\prime }& a_{13}^{\prime }& a_{14}^{\prime }\\ a_{21}^{\prime }& a_{22}^{\prime }& a_{23}^{\prime }& a_{24}^{\prime }\\ a_{31}^{\prime }& a_{32}^{\prime }& a_{33}^{\prime }& a_{34}^{\prime }\\ a_{41}^{\prime }& a_{42}^{\prime }& a_{43}^{\prime }& a_{44}^{\prime }\end{array}\right]$

2. 绕X轴旋转角度为$\theta$。

这一步操作可以通过绕X轴旋转矩阵来实现：

$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{a}_{11}^{\prime }& a_{12}^{\prime }& a_{13}^{\prime }& a_{14}^{\prime }\\ a_{21}^{\prime }& a_{22}^{\prime }& a_{23}^{\prime }& a_{24}^{\prime }\\ a_{31}^{\prime }& a_{32}^{\prime }& a_{33}^{\prime }& a_{34}^{\prime }\\ a_{41}^{\prime }& a_{42}^{\prime }& a_{43}^{\prime }& a_{44}^{\prime }\end{array}\right]=\left[\begin{array}{cccc}{a}_{11}^{\prime \prime }& a_{12}^{\prime \prime }& a_{13}^{\prime \prime }& a_{14}^{\prime \prime }\\ a_{21}^{\prime \prime }& a_{22}^{\prime \prime }& a_{23}^{\prime \prime }& a_{24}^{\prime \prime }\\ a_{31}^{\prime \prime }& a_{32}^{\prime \prime }& a_{33}^{\prime \prime }& a_{34}^{\prime \prime }\\ a_{41}^{\prime \prime }& a_{42}^{\prime \prime }& a_{43}^{\prime \prime }& a_{44}^{\prime \prime }\end{array}\right]$

3. 将矩阵A进行平移，使其回到原来的位置。

这一步操作可以通过平移矩阵来实现：

$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ \frac{a_{11}+a_{21}+a_{31}+a_{41}}{4}& \frac{a_{12}+a_{22}+a_{32}+a_{42}}{4}& \frac{a_{13}+a_{23}+a_{33}+a_{43}}{4}& 1\end{array}\right]\left[\begin{array}{cccc}{a}_{11}^{\prime \prime }& a_{12}^{\prime \prime }& a_{13}^{\prime \prime }& a_{14}^{\prime \prime }\\ a_{21}^{\prime \prime }& a_{22}^{\prime \prime }& a_{23}^{\prime \prime }& a_{24}^{\prime \prime }\\ a_{31}^{\prime \prime }& a_{32}^{\prime \prime }& a_{33}^{\prime \prime }& a_{34}^{\prime \prime }\\ a_{41}^{\prime \prime }& a_{42}^{\prime \prime }& a_{43}^{\prime \prime }& a_{44}^{\prime \prime }\end{array}\right]=\left[\begin{array}{cccc}{b}_{11}& b_{12}& b_{13}& b_{14}\\ b_{21}& b_{22}& b_{23}& b_{24}\\ b_{31}& b_{32}& b_{33}& b_{34}\\ b_{41}& b_{42}& b_{43}& b_{44}\end{array}\right]$

于是，我们得到了4*4矩阵绕X旋转矩阵：

$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ -\frac{a_{11}+a_{21}+a_{31}+a_{41}}{4}& -\frac{a_{12}+a_{22}+a_{32}+a_{42}}{4}& -\frac{a_{13}+a_{23}+a_{33}+a_{43}}{4}& 1\end{array}\right]\left[\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& a_{34}\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ \frac{a_{11}+a_{21}+a_{31}+a_{41}}{4}& \frac{a_{12}+a_{22}+a_{32}+a_{42}}{4}& \frac{a_{13}+a_{23}+a_{33}+a_{43}}{4}& 1\end{array}\right]=\left[\begin{array}{cccc}{b}_{11}& b_{12}& b_{13}& b_{14}\\ b_{21}& b_{22}& b_{23}& b_{24}\\ b_{31}& b_{32}& b_{33}& b_{34}\\ b_{41}& b_{42}& b_{43}& b_{44}\end{array}\right]$

其中，$b_{ij}$表示旋转后的矩阵元素。

3.2 矩阵Y旋转

假设我们要将一个点 $(x,y,z)$ 绕 Y 轴旋转 $\theta$ 角度，那么旋转后的新点坐标为 $(x^{\prime },y^{\prime },z^{\prime })$。

我们可以先将坐标系绕 Y 轴逆时针旋转 $\theta$ 角度，这样点 $(x,y,z)$ 就落在了新的坐标系中。此时，点 $(x^{\prime },y^{\prime },z^{\prime })$ 的坐标就是它在新坐标系中的坐标。然后再将坐标系逆时针旋转 $-\theta$ 角度，这样点 $(x^{\prime },y^{\prime },z^{\prime })$ 就回到了原来的坐标系中。

根据三维坐标系中的旋转矩阵推导公式可知：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 1& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

因此，绕 Y 轴旋转 $\theta$ 角度的矩阵为：

$$\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 1& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$$

3.3 矩阵Z旋转

假设我们有一个4x4的矩阵$M$，它的每个元素为$m_{ij}$，我们想要将它绕着Z轴旋转一个角度$\theta$。为了完成这个任务，我们可以使用下面的矩阵$R$：

$$R=\left[\begin{array}{cccc}\cos (\theta )& -\sin (\theta )& 0& 0\\ \sin (\theta )& \cos (\theta )& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

我们将$M$和$R$相乘，得到一个新的矩阵$M^{\prime }$，它是旋转后的矩阵：

$$M^{\prime }=M\times R$$

这里是具体的推导过程：

1. 我们先考虑矩阵$R$如何作用于矩阵$M$上。为了方便，我们假设$M$的每列分别为$M_1,M_2,M_3,M_4$。那么矩阵$R$作用于$M$上，就相当于将每列旋转一个角度$\theta$，得到新的列向量$M_1^{\prime },M_2^{\prime },M_3^{\prime },M_4^{\prime }$。因此，我们可以将矩阵$R$表示为一个函数$f$，它将列向量$M_i$映射到新的列向量$M_i^{\prime }$：

$$M_i^{\prime }=f(M_i)=R\times M_i$$

2. 现在我们需要将$f$应用于整个矩阵$M$上。考虑到矩阵乘法的性质，我们可以将$f$应用于$M$的每一列，然后将结果拼起来组成新的矩阵$M^{\prime }$：

$$M^{\prime }=[f(M_1),f(M_2),f(M_3),f(M_4)]$$

3. 将$f$代入上式，得到：

$$\begin{array}{rl}{M}^{\prime }& =[R\times M_1,R\times M_2,R\times M_3,R\times M_4]\\ & =\left[\begin{array}{cccc}\cos (\theta )& -\sin (\theta )& 0& 0\\ \sin (\theta )& \cos (\theta )& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{m}_{11}& m_{12}& m_{13}& m_{14}\\ m_{21}& m_{22}& m_{23}& m_{24}\\ m_{31}& m_{32}& m_{33}& m_{34}\\ m_{41}& m_{42}& m_{43}& m_{44}\end{array}\right]\\ & =\left[\begin{array}{cccc}\cos (\theta )m_{11}-\sin (\theta )m_{21}& \cos (\theta )m_{12}-\sin (\theta )m_{22}& \cos (\theta )m_{13}-\sin (\theta )m_{23}& \cos (\theta )m_{14}-\sin (\theta )m_{24}\\ \sin (\theta )m_{11}+\cos (\theta )m_{21}& \sin (\theta )m_{12}+\cos (\theta )m_{22}& \sin (\theta )m_{13}+\cos (\theta )m_{23}& \sin (\theta )m_{14}+\cos (\theta )m_{24}\\ m_{31}& m_{32}& m_{33}& m_{34}\\ m_{41}& m_{42}& m_{43}& m_{44}\end{array}\right]\end{array}$$

因此，将一个4x4的矩阵绕着Z轴旋转一个角度$\theta$，就可以使用上面的矩阵$R$，并将它与原矩阵$M$相乘得到旋转后的矩阵$M^{\prime }$。