线性回归实战1：预测boston房价

boston房价数据集包括506个样本，每个样本包括13个特征变量和该地区的平均房价，房价显然和多个特征变量相关，对于线性回归模型，先选择一元线性回归与多个特征建立线性方程，观察模型预测的好坏，再选择多元线性回归进行房价预测。

简单线性回归：当回归模型包含一个因变量和一个自变量时。
多项式回归：当只有一个自变量，但同时含有变量的幂（X2，X3）时，称为多项式回归。
多元线性回归：当有不止一个自变量时。

 一、加载数据集

1、导包

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import xgboost as xgb
from sklearn import datasets
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import mean_squared_error

2、读入数据并展示

boston = datasets.load_boston()
data = pd.DataFrame(boston.data)
data.columns = boston.feature_names
data['price'] = boston.target
print(data.columns)
print(data.head())

特征（13个）： 

 前几行数据：

3、拆分特征和标签

y = data.pop('price')

二、数据集处理

1、查看空值

print(data.isnull().sum())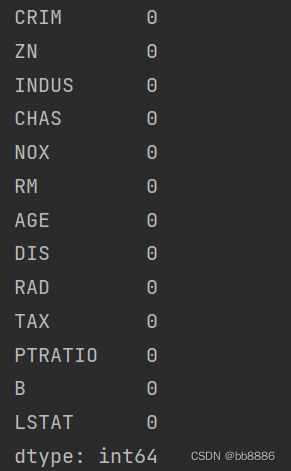

2、查看数据大小

print(data.shape)

3、查看数据描述信息

print(data.describe())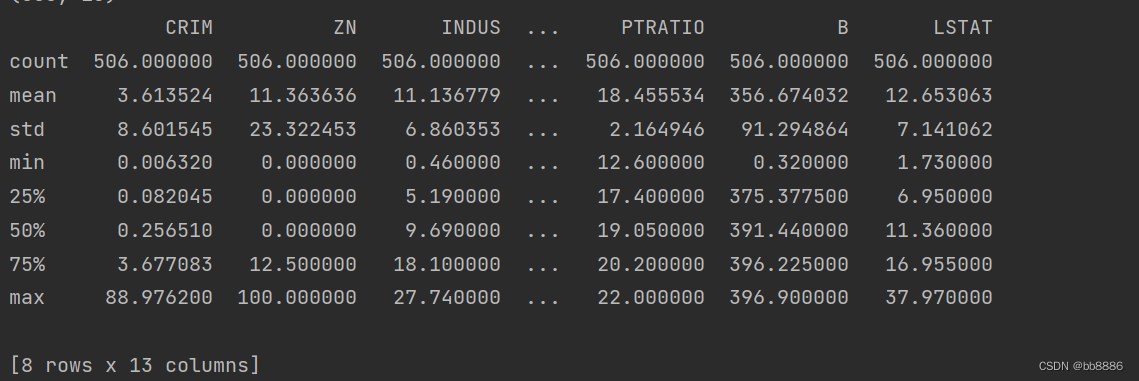

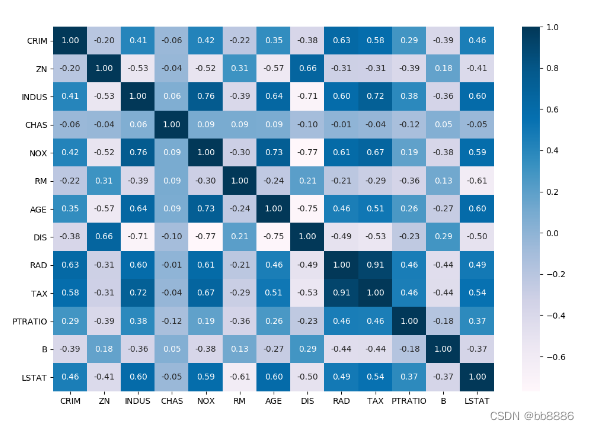
4、查看各特征相关性

import seaborn as sns
plt.figure(figsize=(12, 8))
sns.heatmap(data.corr(), annot=True, fmt='.2f', cmap='PuBu')
plt.show()

5、画出各个特征与房价的散点图

data_xTitle = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B', 'LSTAT']
plt.figure(figsize=[20,18])
fig, a = plt.subplots(5, 3)
m = 0
for i in range(0, 5):
    if i == 4:
        a[i][0].scatter(data[str(data_xTitle[m])], y, s=30, edgecolor='white')
        a[i][0].set_title(str(data_xTitle[m]))
    else:
        for j in range(0, 3):
            a[i][j].scatter(data[str(data_xTitle[m])], y, s=30, edgecolor='white')
            a[i][j].set_title(str(data_xTitle[m]))
            m = m + 1
plt.show()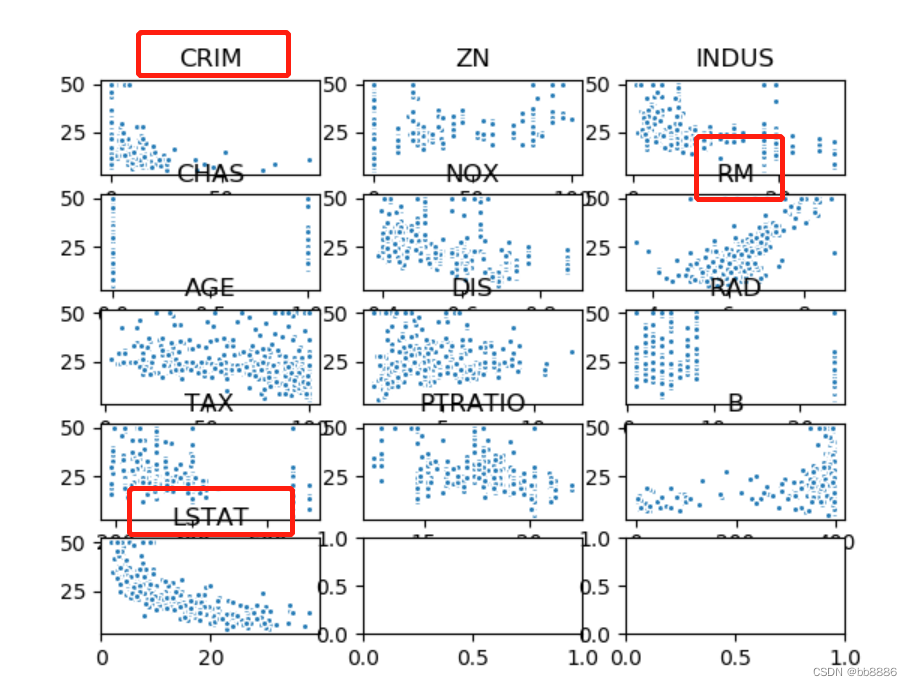

从上图可以看出‘RM’，‘LSTAT’，‘CRIM’三个特征值与房价存在一定的相关性，所以选择该三个特征作为特征值，移除其余不相关的特征值。

new_boston_df = data[['LSTAT', 'CRIM', 'RM']]
print(new_boston_df.describe())
new_boston_df = np.array(new_boston_df)
data = np.array(data)
y = np.array(y)

 6、划分数据集

x_train, x_test, y_train, y_test = train_test_split(data, y, test_size=0.2, random_state=14)

三、建立线性模型

1、建立线性回归模型

我们分别用选择前的特征（13个）和选择后的特征（3个）来建模， 并绘制拟合曲线。

data_list = [data, new_boston_df]


for index, data in enumerate(data_list):
    x_train, x_test, y_train, y_test = train_test_split(data, y, test_size=0.2, random_state=14)

    # 线性回归
    lr_reg = linear_model.LinearRegression()
    lr_reg.fit(x_train, y_train)
    print("线性回归的系数：w = {}, b = {}".format(lr_reg.coef_, lr_reg.intercept_))
    pred = lr_reg.predict(x_test)
    train_pred = lr_reg.predict(x_train)
    # 计算MSE
    test_MSE =mean_squared_error(pred, y_test)
    train_MSE = mean_squared_error(train_pred, y_train)
    # 计算MAE
    test_MAE = mean_absolute_error(y_test, pred)
    train_MAE = mean_absolute_error(y_train, train_pred)
    score = lr_reg.score(x_test, y_test)
    # 预测值与真实值的可视化
    y_test = tuple(y_test)
    test = []
    pre = []
    for i in np.argsort(pred):
        test.append(y_test[i])
        pre.append(pred[i])
    plt.plot(test, label='true')
    plt.plot(pre, label='predict')
    if index == 0:
        plt.title('all_feature,ACC:{:.2f}%,MSE:{:.2f},MAE:{:.2f}'.format(score*100, test_MSE, test_MAE))
    else:
        plt.title('three_feature,ACC:{:.2f}%,MSE:{:.2f},MAE:{:.2f}'.format(score*100, test_MSE, test_MAE))
    plt.legend()
    plt.grid()
    plt.show()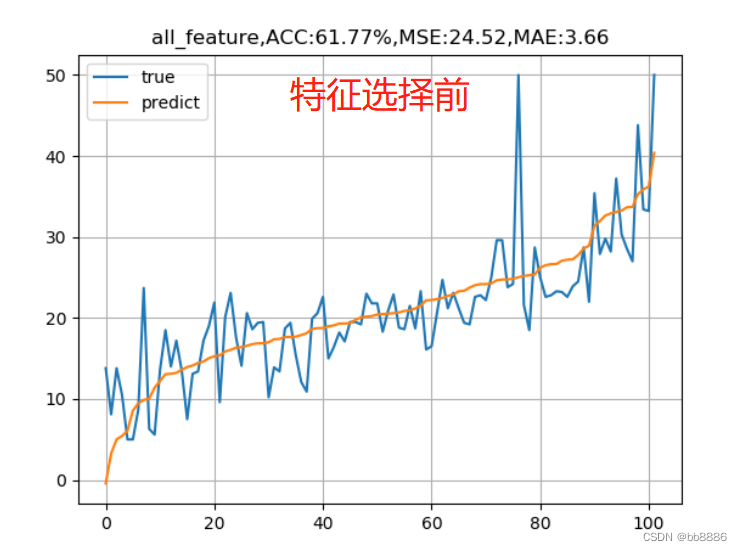

 我们发现，特征选择前的准确率竟然比特征选择后的准确率要高，均方误差也比选择后的要小，这是为什么呢？下面我们分别用特征选择前和特征选择后的特征，使用SDG、岭回归和Lasso回归观察模型结果。

2、SDG

3、岭回归

4、Lasso回归

在上述基础上，我们又增加了两种线性模型，SGD线性模型和线性回归+L2正则化。

1、正规方程求解的线性回归适用于特征不是特别多，不是特别复杂度的数据。

2、SGD线性回归，随机梯度下降线性回归，sgd适用于特征较大，数据量较多的情况，进行自我学习需要设置学习率，默认学习率为0.01，想要更改学习率---learning_rate = 'constant'且eta0=‘要设置的学习率’，梯度方向不需要考虑，因为他是沿着损失减小的方向的，学习率过大会造成梯度爆炸，梯度爆炸出现在复杂的神经网络中，梯度爆炸是损失或准确率全部变成NAN类型，梯度也不能过小，如果过小，会造成原地打转，此时梯度消失，--损失不减小，一直那么大。

学习率如何设置？一般为0.1、0.01或0.001，不能过大或过小。

3、线性回归+L2正则化，岭回归。（让某些特征值的权重趋于0），在小的数据集上效果会比LinearRegression效果好一些，正规方程求解的线性回归特征不是特别多，不是特别复杂度的数据 。

data_list = [data, new_boston_df]
model_lists = {'LinearRegression': linear_model.LinearRegression(),
               'SGDRegressor': linear_model.SGDRegressor(),
               'Ridge': Ridge()}
for index, data in enumerate(data_list):
    x_train, x_test, y_train, y_test = train_test_split(data, y, test_size=0.2, random_state=14)
    for name, model in model_lists.items():
        # 线性回归
        lr_reg = model
        lr_reg.fit(x_train, y_train)
        print("线性回归的系数：w = {}, b = {}".format(lr_reg.coef_, lr_reg.intercept_))
        pred = lr_reg.predict(x_test)
        train_pred = lr_reg.predict(x_train)
        # 计算MSE
        test_MSE =mean_squared_error(pred, y_test)
        train_MSE = mean_squared_error(train_pred, y_train)
        # 计算MAE
        test_MAE = mean_absolute_error(y_test, pred)
        train_MAE = mean_absolute_error(y_train, train_pred)
        score = lr_reg.score(x_test, y_test)
        # 预测值与真实值的可视化
        y_test = tuple(y_test)
        test = []
        pre = []
        for i in np.argsort(pred):
            test.append(y_test[i])
            pre.append(pred[i])
        plt.plot(test, label='true')
        plt.plot(pre, label='predict')
        if index == 0:
            plt.title('all_feature,{}, ACC:{:.2f}%,MSE:{:.2f},MAE:{:.2f}'.format(name, score*100, test_MSE, test_MAE))
        else:
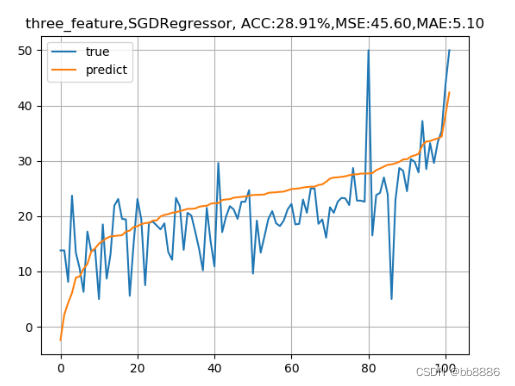
            plt.title('three_feature,{}, ACC:{:.2f}%,MSE:{:.2f},MAE:{:.2f}'.format(name, score*100, test_MSE, test_MAE))
        plt.legend()
        plt.grid()
        plt.show()