假设检验与抽样分布的联系

本文先给出假设检验和抽样分布的定义，然后，以一个正态总体的均值抽样分布为例，介绍假设检验的过程，最后拓展到其他抽样分布的情况并总结。

1 假设检验

假设检验（hypothesis test）又称为显著性检验（significance test），是根据总体的理论分布和小概率理论，对未知或不完全知道的总体提出两种彼此对立的假设，然后由样本的实际结果，经过一定的计算，作出在一定概率意义上应该接受的那种假设的推断。如果抽样结果使小概率事件发生，则拒绝假设；如果抽样结果没有使小概率事件发生，则接受假设。

2 抽样分布

定义：从一个总体中，独立随机地抽取一定数目的样本，所得到的样本各种统计量的概率分布。

2.1 举例说明抽样分布的实际含义

假设现在有一个年级的学生，我们每次从中随机抽取10名学生，测量身高，计算它们的均值。重复上面的操作50次。这样，我们就得到了50个均值，然后我们可以画出均值的频率分布图。这就是一个抽样分布。

3 一个正态总体均值的抽样分布 & 假设检验

在统计学中，常常假设总体是服从正态分布的。因为基于这个条件，抽样分布的性质很明确。

如果从一个总体$N(μ,σ^2)$中独立随机地抽取$n$个样本，那么$\bar X\sim N(μ,\frac {σ^2}{n})$，也写做$\frac{\bar X-μ}{σ ⁄ \sqrt n} \sim N(0,1)$。

这个的定义是什么意思呢？举个例子，自变量X的值服从正态分布$N(μ,σ^2)$。如图1所示，就是指$X$变量取不同数值的概率是一个正态函数。然后，随机取值$n$个，得到观察值$x_1,x_2,…,x_n$，计算其平均值。如果，不断重复上面的随机取值，我们就可以得到很多个抽样的平均值。此时，通过理论计算，得出这些平均值$\bar X$同样服从正态分布，只是方差变成$\frac{σ^2}{n}$。这很容易理解，因为如果抽样的数目是总体的数目，得到的均值不就是总体的均值嘛！方差也就变成了0。

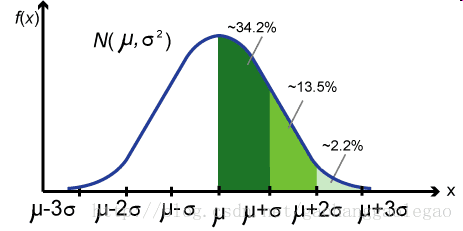
图1 正态分布

趁热打铁，举一个例题。
根据长期的经验和资料的分析，某砖瓦厂所生产的砖的“抗断强度”服从正态分布，方差$σ^2$=1.21。现在从该厂生产的一批砖中，随机抽取6块，测得抗断强度（kg/cm2）如下：
32.56 29.66 31.64 30.00 31.87 31.03
问这一批砖的平均抗断强度可否认为是32.50（kg/cm2）？

首先，我们得做出对总体的假设。这里，总体就是那一批砖，样本就是随机抽取出来的6块砖。所以，我们提出假设H0: 可以认为那一批砖的平均抗断强度为32.50。H1: 不可以认为平均抗断强度为32.50。

在假设之后，我们就有了总体正态分布$N(μ,σ^2)$的参数$μ=32.50$，$σ^2=1.21$。根据前面的知识，我们也知道抽样的均值也服从正态分布$X \sim N(μ,\frac {σ^2}{n})$，即$\bar X \sim N(32.5,0.2)$，如图2所示。

图2 均值的抽样分布函数

接着，就到了检验的环节了。如果总体的情况真的是这样，那么这组实际抽样得到数据是不是很合理呢？在这里，就是指，这组数据的平均值不是离中心值32.50比较近。
我们来算一算这组数据的平均值。

$\bar X=1/6 (32.56+29.66+31.64+30+31.87+31.03)=31.13$

在图2中，就是红色线代表的位置。直观的感觉，并不是很大的概率会出现这样的结果，因为在红色线左边的面积很小，意味着出现这个数值的可能性很小。

总结成一段话：抽样分布是我们用来对假设进行检验的工具，在不同情况下，我们需要使用不同的工具，但是思路都是一致的。当我们对总体提出假设后，理论上的抽样分布就已经得到了，然后，我们要做的就是计算样本的数据的出现是否属于小概率事件。如果是，我们就否定原假设；如果不是，则保留原假设。