m 序列(最长线性反馈移位寄存器序列)详解

本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。

m 序列 (最长线性反馈移位寄存器序列)

线性反馈移位寄存器的特征多项式

线性反馈移位寄存器的递推关系式

递推关系式又称为反馈逻辑函数或递推方程。设图2所示的线性反馈移位 寄存器的初始状态为 $(a_0{a}_1\dots a_{n-2}{a}_{n-1})$ , 经一次移位线性反馈, 移位寄存器 左端第一级的输入为
$$a_n=c_1{a}_{n-1}+c_2{a}_{n-2}+\cdots +c_{n-1}{a}_1+c_n{a}_0=\sum _{i=1}^n{c}_i{a}_{n-i}$$

若经 $\mathbf{k}$ 次移位, 则第一级的输入为
$$a_l=\sum _{i=1}^n{c}_i{a}_{l-i}$$
其中, $l=n+k-1\ge n,k=1,2,3,\dots$
由此可见, 移位寄存器第一级的输入, 由反馈逻辑及移位寄存器的原状态所决定。上式称为递推关系式。

线性反馈移位寄存器的特征多项式

用多项式 f(x) 来描述线性反馈移位寄存器的反馈连接状态:
$$f(x)=c_0+c_{1}x+\cdots +c_n{x}^n=\sum _{i=0}^n{c}_i{x}^i$$
称为特征多项式或特征方程。其中, $x^i$ 存在, 表明 $c_i=1$ , 否则 $c_i=0$ , x 本身的取值并无实际意义。 $c_i$ 的取值决定了移位寄存器的反馈连接。 由于 $c_0=c_n=1$ , 因此, f(x) 是一个常数项为 1 的 n 次多项式, n 为移位寄存器级数。

一个 n 级线性反馈移位寄存器能产生 m 序列的充要条件是它的特征 多项式为一个 n 次本原多项式。若一个 n 次多项式 f(x) 满足下列条件:

(1) f(x) 为既约多项式(即不能分解因式的多项式);

(2) f(x) 可整除 $(x^p+1),p^n-1$ ;

(3) f(x) 除不尽 $(x^{q+1}),q<p$ 。

则称 f(x) 为本原多项式。以上为我们构成 m 序列提供了理论根据。

m序列产生器

用线性反馈移位寄存器构成 m 序列产生器, 关键是由特征多项式 f(x) 来确定反馈 线的状态, 而且特征多项式 f(x) 必须是本原多项式。

现以 n=4 为例来说明 m 序列产生器的构成。用4级线性反馈移位寄存器产生的 m 序列, 其周期为$p=2^4-1=15$ , 其特征多项式 f(x) 是 4 次本原多项式，能整除 $(x^{15}+1)$ 。先将 $(x^{15}+1)$ 分解因式, 使各因式为既约多项式, 再寻找 f(x) 。
$$\begin{array}{rl}{x}^{15}+1& =(x+1)(x^2+x+1)(x^4+x+1)\\ & \cdot (x^4+x^3+1)(x^4+x^3+x^2+x+1)\end{array}$$
其中, 4 次既约多项式有 3 个, 但 $(x^4+x^3+x^2+x+1)$ 能整除 $(x^5+1)$ , 故它不是本原多 项式。因此找到两个4次本原多项式 $(x^4+x+1)$ 和 $(x^4+x^3+1)$ 。由其中任何一个都可 产生 m 序列。用 $\mathrm{f}(\mathrm{x})=({\mathrm{x}}^4+\mathrm{x}+1)$ 构成的 $\mathrm{m}$ 序列产生器如图所示。

设4级移位寄存器的初始状态为 1000 ,$c_4=c_1=c_0=1,c_3=c_2=0$ 。输出序列 { a k } \{a_{k}\} { ak​} 的周期长度为 15 。

m序列的性质

均衡特性(平衡性)

m 序列每一周期中 1 的个数比 0 的个数多 1 个。由于 $p=2^n-1$ 为奇 数, 因而在每一周期中 1 的个数为 $(p+1)/2=2^{n-1}$ (偶数), 而 0 的 个数为 $(p-1)/2=2^{n-1}-1$ (奇数)。上例中 p=15,1 的个数为 8,0 的个 数为 7。当p足够大时, 在一个周期中 1 与 0 出现的次数基本相等。

游程特性(游程分布的随机性)

我们把一个序列中取值(1 或 0)相同连在一起的元素合称为一个游程。在一个游程中元素的个数称为游程长度。例如图中给出的 $\mathbf{m}$ 序列

在其一个周期的 15 个元素中, 共有 8 个游程
长度为 4 的游程 1 个, 即 1111 ;
长度为 3 的游程 1 个, 即 000 ;
长度为 2 的游程 2 个, 即 11 与 00 ;
长度为 1 的游程 4 个, 即 2 个 1 与 2 个 0 。

m 序列的一个周期 $(p=2^{n-1})$ 中, 游程总数为 $2^{n-1}$ 。

长度为 1 的游程个数占游程总数的 1 / 2 ; 长度为 2 的游程个数占游 程总数的 $1/2^2=1/4$ ; 长度为 3 的游程个数占游程总数的 $1/2^3=1/8$ 等等。

一般地, 长度为k的游程个数占游程总数的 $1/2^k=2^{-k}$ , 其 中 $1\le k\le (n-2)$ 。而且, 在长度为k的游程中, 连1游程与连0游程各占一半, 长为 (n-1) 的游程是连0游程, 长为n的游程是连1游程。

移位相加特性(线性叠加性)

$\mathbf{m}$ 序列和它的位移序列模二相加后所得序列仍是该 $\mathbf{m}$ 序列的某个 位移序列。设 $m_r$ 是周期为 p 的 m 序列 $m_p$ 的 r 次延迟移位后的序列, 那么
$$m_p\oplus m_r=m_s$$
其中, $m_s$ 为 $m_p$ 某次延迟移位后的序列。例如，
$$m_p=000111101011001,\dots$$

$m_p$ 延迟两位后得 $m_r$ , 再模二相加
$$\begin{array}{l}{m}_r=010001111010\\ m_{\mathrm{s}}={\mathbf{m}}_{\mathrm{p}}\oplus {\mathbf{m}}_r=010110,\dots \end{array}$$
可见, $m_{\mathrm{s}}=m_{\mathrm{p}}\oplus m_r$ 为 $m_p$ 延迟 8 位后的序列。

自相关特性

$\mathbf{m}$ 序列具有非常重要的自相关特性。在 $\mathbf{m}$ 序列中, 常常用 +1 代表 0 , 用-1代表 1。此时定义：设长为 p 的 $\mathbf{m}$ 序列, 记作
$$a_1,a_2,a_3,\dots ,a_p(p=2^{n-1})$$
经过 $\mathbf{j}$ 次移位后, $\mathbf{m}$ 序列为
$$a_{j+1},a_{j+2},a_{j+3},\dots ,a_{j+p}$$
其中, $a_{i+p}=a_i$ (以 p 为周期), 以上两序列的对应项相乘然后相加, 利用所得的总和
$$a_1\cdot a_{j+1}+a_2\cdot a_{j+2}+a_3\cdot a_{j+3}+\cdots +a_p\cdot a_{j+p}=\sum _{i=1}^p{a}_i{a}_{j+i}$$
来衡量一个 m 序列与它的 j 次移位序列之间的相关程度, 并把它叫 做 $\mathbf{m}$ 序列 $(a_1,a_2,a_3,\dots ,a_p)$ 的自相关函数。记作
$$R(j)=\sum _{i=1}^p{a}_i{a}_{j+i}$$
当采用二进制数字 0 和 1 代表码元的可能取值时, 上式可表示为
$$R(j)=\frac{A-D}{A+D}=\frac{A-D}{p}$$
式中, A、D分别是 $\mathbf{m}$ 序列与其 j 次移位的序列在一个周期中对应元素相同、不相同的数目, 还可以改写为
$$R(j)=\frac{[a_i\oplus a_{i+j}=0]\text{ 的数目 }-[a_i\oplus a_{i+j}=1]\text{ 的数目 }}{p}$$

由移位相加特性可知, $a_i\oplus a_{i+j}$ 仍是 m 序列中的元素, 所以式分子就等于 m 序列中一个周期中 0 的数目与 1 的数目之差。另外由 $\mathbf{m}$ 序列的均衡性可知, 在一个周期中 0 比 1 的个数少一个, 故得 $A-D=-1$ ( j 为非零整数时) 或 p(j为零时) 。因此得
R ( j ) = { 1 j = 0 − 1 p j = ± 1 , ± 2 , … , ± ( p − 1 ) . R(j)=\{\begin{array}{ll} 1 & j=0 \\ \frac{-1}{p} & j=\pm 1, \pm 2, \ldots, \pm(p-1) \end{array}. R(j)={ 1p−1​​j=0j=±1,±2,…,±(p−1)​.

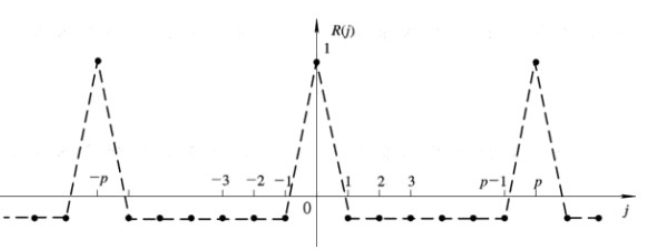
$\mathrm{m}$序列的自相关函数只有两种取值 (1 和 -1 / p) 。 R(j) 是一个周期函数, 即
$$\mathbf{R}(j)=\mathbf{R}(j+kp)$$
式中, $k=1,2,\dots ,p=(2^n-1)$ 为周期。而且 $R(j)$ 是偶函数, 即
$$R(j)=R(-j)j=\text{ 整数 }$$

伪噪声特性

如果我们对一个正态分布白噪声取样，若取样值为正，记为+1，

若取样值为负，记为-1，将每次取样所得极性排成序列，可以写成 …+1,-1,+1,+1,+1,-1,-1,+1,-1,…

这是一个随机序列，它具有如下基本性质:(1)序列中+1和-1出现的概率相等;

序列中长度为 1 的游程约占 1 / 2 , 长度为 2 的游程约占 1 / 4 , 长度为 3 的游程约占 1 / 8, $\dots$ 一般地, 长度为 $\mathrm{k}$ 的游程约占 $1/2^k$ , 而且 +1 、-1 游程的数目各占一半;

由于白噪声的功率谱为常数, 因此其自相关函数为一冲击函数 $\delta (\tau )$ 。 把 $\mathbf{m}$ 序列与上述随机序列比较, 当周期长度 $\mathbf{p}$ 足够大时, $\mathbf{m}$ 序列与随机序列的性质是十分相似的。可见, $\mathbf{m}$ 序列是一种伪喿声特性较好的伪随机序列, 且易产生, 因此应用十分广泛。

参考文献：

1. Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
2. Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
3. 周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
4. 樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.