目录
RepVGG: Making VGG-style ConvNets Great Again(RepVGG:让vgg风格的ConvNets再次伟大)
参考链接
- RepVGG网络简介
- RepVGG:使VGG样式的ConvNets再次出色
- RepVGG:一个结构重参数化网络
- 向chatgpt提问,辅助理解:chatgpt-poe
结构重参数化的实质
结构重参数化就是训练和推理使用不同的结构,但是用同一套参数量
结构重参数化的实质:训练时的结构对应一组参数,推理时我们想要的结构对应另一组参数;只要能把前者的参数等价转换为后者,就可以将前者的结构等价转换为后者
猜想:那所以,结构重参数化,应该只是对推理时候有用吧?其实训练时的多分支结构设计就已经有效了,现在考虑重参数化,应该只是为了量化部署吧?
3.1. Simple is Fast, Memory-economical, Flexible 简单就是快速,节省内存,灵活
使用简单的ConvNets至少有三个原因:
- 快速
- 节省内存
- 灵活
3.2 Training-time Multi-branch Architecture 培训时-多分支架构
在深度学习中,shortcut通常指的是"跳跃连接"或"残差连接"。它是一种网络结构设计方法,在网络中引入一条额外的直接连接,将输入的信息直接传递到输出端,从而避免了信息在网络中的丢失和扭曲。shortcut连接可以帮助网络更好地学习到输入和输出之间的映射关系,从而提高网络的性能和收敛速度。shortcut连接常用于卷积神经网络(CNN)和残差神经网络(ResNet)等深度学习模型中。
我们的结构重参数化方法受到 ResNet 的启发,它显式构造了一个残差连接分支,将信息流建模为 y = x + f ( x ) y = x +f(x) y=x+f(x),并使用残差块学习 f f f。当 x x x 和 f ( x ) f(x) f(x) 的维数不匹配时,它变成 y = g ( x ) + f ( x ) y = g(x)+f(x) y=g(x)+f(x) ,其中 g ( x ) g(x) g(x) 是一个由 1×1 conv 实现的卷积残差连接。ResNets成功的一个解释是,这样的多分支架构使得模型成为众多较浅模型[36]的隐式集合。具体来说,有了 n n n 个块,模型可以被解释为 2 n 2^n 2n 个模型的集合,因为每个块将流分支成两条路径。
由于多分支拓扑在推理方面存在缺陷,但分支似乎有利于训练[36],因此我们使用多个分支来对众多模型进行仅训练时的集成。为了使大多数成员更浅薄或更简单,我们使用类似 ResNet 的Identity(仅当尺寸匹配时)和1 × 1分支,使一个构建块的训练时的信息流为 y = x + g ( x ) + f ( x ) y = x + g(x) + f(x) y=x+g(x)+f(x)。我们只是简单地将几个这样的模块堆叠起来,来构建训练时的模型。从与[36]相同的角度来看,模型是由 3 n 3^n 3n 个成员和 n n n 个这样的块组成的集合。
结论:在训练时,仅使用多个分支堆叠的RepVGG模块(仿照VGG网络堆叠,多个分支即3个分支= 3 × 3 c o n v + 1 × 1 c o n v + i d e n t i t y 3×3conv+1×1conv+identity 3×3conv+1×1conv+identity)
摘录自RepVGG网络简介
由于论文中的图都是简化过的,于是我自己根据源码绘制了下图的RepVGG Block(注意是针对训练时采用的结构)。其中图(a)是进行下采样(stride=2)时使用的RepVGG Block结构,图(b)是正常的(stride=1)RepVGG Block结构。通过图(b)可以看到训练时RepVGG Block并行了三个分支:一个卷积核大小为3x3的主分支,一个卷积核大小为1x1的shortcut分支以及一个只连了BN的shortcut分支

3.3 Re-param for Plain Inference-time Model 推理时-模型重参数
结论:推理时将多分支模型转换成单路模型,即使用单个3×3卷积层来代替原本的块
下面的内容如何理解?
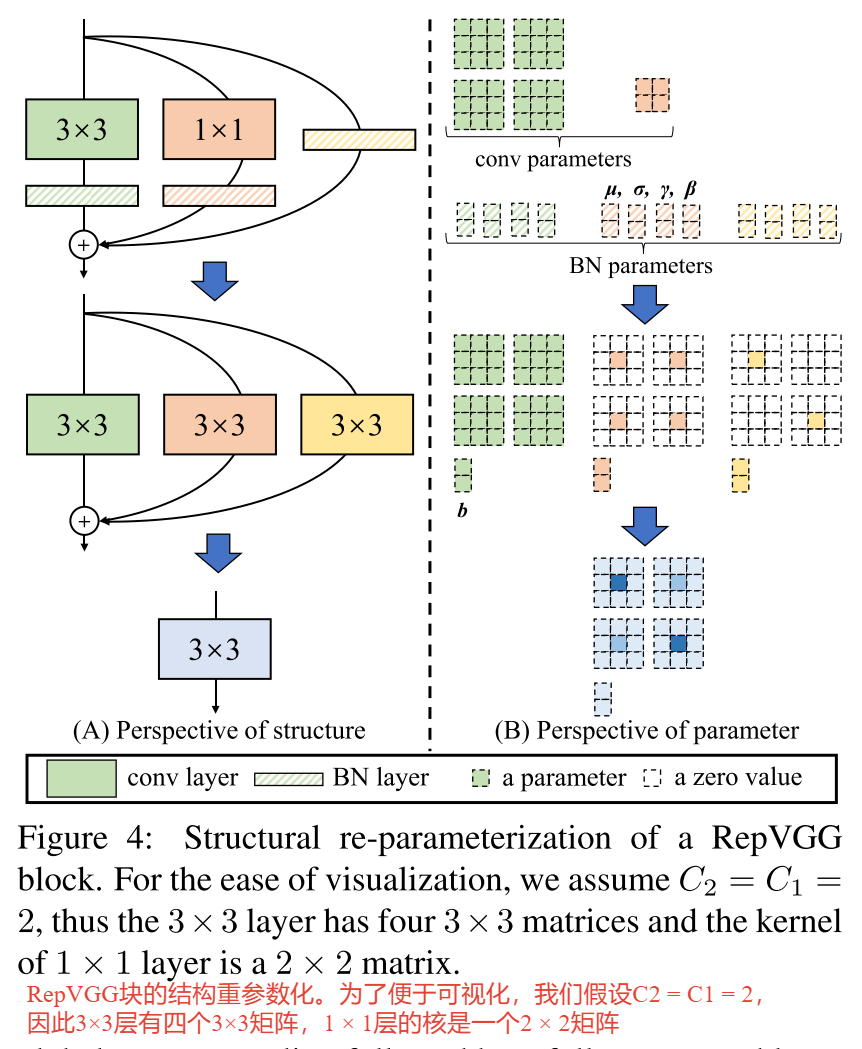
在本小节中,我们将描述如何将一个经过训练的块转换为一个3×3 conv层进行推理。需要注意的是,在相加之前,每个分支都使用BN(图4)。形式上,我们用 W ( 3 ) ∈ R C 2 × C 1 × 3 × 3 \mathrm{W}^{(3)} \in \mathbb{R}^{C_2 \times C_1 \times 3 \times 3} W(3)∈RC2×C1×3×3表示3×3 conv层的核, C 1 C_1 C1输入通道, C 2 C_2 C2输出通道,而 W ( 1 ) ∈ R C 2 × C 1 \mathrm{W}^{(1)} \in \mathbb{R}^{C_2 \times C_1 } W(1)∈RC2×C1 表示1× 1分支的核。
- 我们使用 µ ( 3 ) µ^{(3)} µ(3), σ ( 3 ) {\sigma}^{(3)} σ(3), γ ( 3 ) {\gamma}^{(3)} γ(3), β ( 3 ) {\beta}^{(3)} β(3)作为 3 × 3 conv 后 B N BN BN 层的累积均值、标准差和学习的标度因子和偏差
- µ ( 1 ) µ^{(1)} µ(1), σ ( 1 ) {\sigma}^{(1)} σ(1), γ ( 1 ) {\gamma}^{(1)} γ(1), β ( 1 ) {\beta}^{(1)} β(1)作为 1 × 1 conv 后 B N BN BN 层的值
- µ ( 0 ) µ^{(0)} µ(0), σ ( 0 ) {\sigma}^{(0)} σ(0), γ ( 0 ) {\gamma}^{(0)} γ(0), β ( 0 ) {\beta}^{(0)} β(0)作为 恒等分支(Identity branch) 后 B N BN BN 层的值
设 M ( 1 ) ∈ R N × C 1 × H 1 × W 1 \mathrm{M}^{(1)} \in \mathbb{R}^{N \times C_1 \times H_1 \times W_1} M(1)∈RN×C1×H1×W1, M ( 2 ) ∈ R N × C 2 × H 2 × W 2 \mathrm{M}^{(2)} \in \mathbb{R}^{N \times C_2 \times H_2 \times W_2} M(2)∈RN×C2×H2×W2 分别是输入和输出,∗是卷积算子。如果 C 1 = C 2 , H 1 = H 2 , W 1 = W 2 C_1 = C_2, H_1 = H_2, W_1 = W_2 C1=C2,H1=H2,W1=W2,我们有
M ( 2 ) = bn ( M ( 1 ) ∗ W ( 3 ) , μ ( 3 ) , σ ( 3 ) , γ ( 3 ) , β ( 3 ) ) + bn ( M ( 1 ) ∗ W ( 1 ) , μ ( 1 ) , σ ( 1 ) , γ ( 1 ) , β ( 1 ) ) + bn ( M ( 1 ) , μ ( 0 ) , σ ( 0 ) , γ ( 0 ) , β ( 0 ) ) . \begin{aligned} \mathrm{M}^{(2)} & =\operatorname{bn}\left(\mathrm{M}^{(1)} * \mathrm{~W}^{(3)}, \boldsymbol{\mu}^{(3)}, \boldsymbol{\sigma}^{(3)}, \boldsymbol{\gamma}^{(3)}, \boldsymbol{\beta}^{(3)}\right) \\ & +\operatorname{bn}\left(\mathrm{M}^{(1)} * \mathrm{~W}^{(1)}, \boldsymbol{\mu}^{(1)}, \boldsymbol{\sigma}^{(1)}, \boldsymbol{\gamma}^{(1)}, \boldsymbol{\beta}^{(1)}\right) \\ & +\operatorname{bn}\left(\mathrm{M}^{(1)}, \boldsymbol{\mu}^{(0)}, \boldsymbol{\sigma}^{(0)}, \boldsymbol{\gamma}^{(0)}, \boldsymbol{\beta}^{(0)}\right) .\end{aligned} M(2)=bn(M(1)∗ W(3),μ(3),σ(3),γ(3),β(3))+bn(M(1)∗ W(1),μ(1),σ(1),γ(1),β(1))+bn(M(1),μ(0),σ(0),γ(0),β(0)).
chatgpt答:
这段内容是在讲述如何将一个经过训练的块转换为一个3×3卷积层进行推理。该块包含了三个分支,每个分支都使用了批归一化(BN)层,其中一个分支是恒等分支。具体地,该块的结构如下:
/ - 1x1 conv - BN - ReLU - 3x3 conv - BN - ReLU -
/ \
input ----- + ---- output
\ /
\ - ----------------------- 1x1 conv - BN --------- /
该段文字中的公式 M ( 2 ) = bn ( M ( 1 ) ∗ W ( 3 ) , μ ( 3 ) , σ ( 3 ) , γ ( 3 ) , β ( 3 ) ) + bn ( M ( 1 ) ∗ W ( 1 ) , μ ( 1 ) , σ ( 1 ) , γ ( 1 ) , β ( 1 ) ) + bn ( M ( 1 ) , μ ( 0 ) , σ ( 0 ) , γ ( 0 ) , β ( 0 ) ) \mathrm{M}^{(2)}=\operatorname{bn}\left(\mathrm{M}^{(1)} * \mathrm{~W}^{(3)}, \boldsymbol{\mu}^{(3)}, \boldsymbol{\sigma}^{(3)}, \boldsymbol{\gamma}^{(3)}, \boldsymbol{\beta}^{(3)}\right)+\operatorname{bn}\left(\mathrm{M}^{(1)} * \mathrm{~W}^{(1)}, \boldsymbol{\mu}^{(1)}, \boldsymbol{\sigma}^{(1)}, \boldsymbol{\gamma}^{(1)}, \boldsymbol{\beta}^{(1)}\right)+\operatorname{bn}\left(\mathrm{M}^{(1)}, \boldsymbol{\mu}^{(0)}, \boldsymbol{\sigma}^{(0)}, \boldsymbol{\gamma}^{(0)}, \boldsymbol{\beta}^{(0)}\right) M(2)=bn(M(1)∗ W(3),μ(3),σ(3),γ(3),β(3))+bn(M(1)∗ W(1),μ(1),σ(1),γ(1),β(1))+bn(M(1),μ(0),σ(0),γ(0),β(0))描述了将该块转换为一个3×3卷积层的具体计算过程。其中, M ( 1 ) \mathrm{M}^{(1)} M(1)是该块的输入, M ( 2 ) \mathrm{M}^{(2)} M(2)是该块的输出, W ( 1 ) \mathrm{~W}^{(1)} W(1)和 W ( 3 ) \mathrm{~W}^{(3)} W(3)分别是1×1卷积层和3×3卷积层的卷积核, bn \operatorname{bn} bn表示批归一化操作, μ ( 0 ) , σ ( 0 ) , γ ( 0 ) , β ( 0 ) \boldsymbol{\mu}^{(0)}, \boldsymbol{\sigma}^{(0)}, \boldsymbol{\gamma}^{(0)}, \boldsymbol{\beta}^{(0)} μ(0),σ(0),γ(0),β(0)、 μ ( 1 ) , σ ( 1 ) , γ ( 1 ) , β ( 1 ) \boldsymbol{\mu}^{(1)}, \boldsymbol{\sigma}^{(1)}, \boldsymbol{\gamma}^{(1)}, \boldsymbol{\beta}^{(1)} μ(1),σ(1),γ(1),β(1)和 μ ( 3 ) , σ ( 3 ) , γ ( 3 ) , β ( 3 ) \boldsymbol{\mu}^{(3)}, \boldsymbol{\sigma}^{(3)}, \boldsymbol{\gamma}^{(3)}, \boldsymbol{\beta}^{(3)} μ(3),σ(3),γ(3),β(3)分别是三个批归一化层的均值、方差、缩放因子和偏移量。公式中的加号表示相加操作。
该公式的计算过程是将该块中的三个分支通过卷积和批归一化操作,逐层提取特征,并将三个分支的特征相加。具体地,首先将输入 M ( 1 ) \mathrm{M}^{(1)} M(1)分别通过1×1卷积核和3×3卷积核进行卷积操作,并分别对卷积后的结果进行批归一化处理,得到两个归一化后的特征图。然后,将这两个特征图相加,并对相加后的结果再次进行批归一化处理,得到最终的输出 M ( 2 ) \mathrm{M}^{(2)} M(2)。
需要注意的是,该公式中的三个批归一化层分别使用了不同的均值、方差、缩放因子和偏移量,这些值都是在训练过程中学习得到的。同时,如果该块的输入输出通道数以及高度和宽度都相同,即C1=C2,H1=H2,W1=W2,那么我们就可以使用单个3×3卷积层来代替原本的块,从而提高推理效率。
Make RepVGG Greater Again: A Quantization-aware Approach(让RepVGG再次变大:量化感知的方法)
参考链接
QARepVGG (quantized-aware RepVGG, 量化感知RepVGG)
下面右图中的红色斜杠应该是ReLU

量化的定义:量化。网络量化是一种有效的模型压缩方法,它将网络权值和输入数据映射到较低的精度(通常为8位)以进行快速计算,这大大降低了模型的大小和计算成本。在不影响性能的情况下,量化主要用于提高部署前的速度,在工业生产中作为事实上的标准。训练后量化(PTQ)是最常用的方案,因为它只需要几批图像来校准量化参数,而且不需要额外的训练。量化感知训练(quantification -aware Training, QAT)方法也被提出以提高量化精度,如纯整数算术量化[24],无数据量化[32],硬件感知量化[42],混合精度量化[43],零射量化[3]。由于QAT通常涉及到对培训代码的入侵,并且需要额外的成本,因此它只在培训代码在手边且PTQ不能产生令人满意的结果时才使用。为了更好地展示所提出的量化感知体系结构,我们主要使用PTQ来评估量化精度。同时,我们通过实验来证明它对QAT也是有益的。
3. Make Reparameterization Quantization Friendly 使重参数化量化友好
对于基于重参数化的体系结构,有两个主要组件,权重和激活,它们需要量化,并可能导致准确性下降。激活还作为下一层的输入,因此错误一层一层地增加。因此,神经网络良好的量化性能主要需要两个基本条件:
- 权值分布有利于量化
- 激活分布(即模型如何响应输入特征)是可处理的量化
根据经验,违反其中任何一种都会导致较差的量化性能。