一、思想
高斯牛顿法的对象是最小二乘法。
采用一定的方法对Hession 矩阵进行近似,这样的话可以减少计算量,只需要计算一阶偏导数得到雅可比矩阵即可。
minF(x)=|| f(x)||^2
那么x在xk处的增量Δxk出的最小二乘法为
minF(xk+Δxk)=∣∣f(xk+Δxk)∣∣^2
同理:
F(xk+Δxk)=≈∣∣f(xk)+J(xk)TΔxk∣∣^2
J(xk) 是一阶导数,也就是雅可比矩阵,xk是一个已知数据,只有Δxk是未知数,那么我们要计算的就是这个Δxk。
二、算法流程
1、确定函数的模型,设定迭代精度m
2、设定一个初始值 y=A*exp(Bx), 已知x y 数据,所以拟合的就是参数 A 和B,那么就要给A 和B 设定一个初始值。
3、对与k次迭代,计算J(xk)雅可比矩阵 和 误差r
y'=A*exp(Bx), r=y-y'
4、计算 Δxk=inv(J(xk)'J(xk)T)*(-J(xk)*r)
5、计算 norm(Δxk) <m?Ok:x(k+1)=x(x)+Δxk ---》返回3
eg1 :

clear ;
clc;
iterator_num=500;
segma=1e-8;% 迭代精度
% y=a*exp(bx)+c 函数模型
% 设置其实参数值
a=6;
b=0.3;
c=0.1;
act_x=[1;2;3;4;5;6;7;8];
act_y=[8.3;11.0;14.7;19.7;26.7;35.2;44.4;55.9];
% 开始迭代
for i=1:iterator_num
y=a*exp(b*act_x);
%计算误差 r=act_y-y
r=act_y-y;
% 计算偏导数a 的雅可比矩阵
Jacobian_a=exp(b*act_x);
% 计算偏导数b 的雅可比矩阵
Jacobian_b=a*exp(b*act_x).*act_x;
% 联立雅可比方阵
Jf=[Jacobian_a,Jacobian_b];
% =====
delta_abc=inv(Jf'*Jf)*Jf'*r;
if norm(delta_abc)<segma
break;
end
a_iterator=a+delta_abc(1);
b_iterator=b+delta_abc(2);
% 判断精度
if norm(r)<segma
break;
end
a=a_iterator;
b=b_iterator;
end
it_y=a*exp(b*act_x);
plot(act_x,act_y,'.',act_x,it_y,'-');
xlim([0 10]);
ylim([0 70]);
legend('act','fit','Location','southoutside','Orientation','horizontal')

eg2;
Matlab Gauss 拟合_Σίσυφος1900的博客-CSDN博客
从上面的链接可以得到一些数据x y

函数的模型是:y(i)=a*exp(-(x(i)-b).^2/c.^2)+0.1*rand(1);
补充:求导数
>> syms act_x
>> y=a*exp(-(act_x-b).^2/c.^2)
y =
a*exp(-(act_x - b)^2/c^2)
>> diff_a=diff(y,a)
diff_a =
exp(-(act_x - b)^2/c^2)
>> diff_b=diff(y,b)
diff_b =
(a*exp(-(act_x - b)^2/c^2)*(2*act_x - 2*b))/c^2
>> diff_c=diff(y,c)
diff_c =
(2*a*exp(-(act_x - b)^2/c^2)*(act_x - b)^2)/c^3
>> 拟合效果:

% 牛顿高斯迭代系数
% 牛顿高斯迭代系数
close all;
clear;
clc;
% y(i)=a*exp(-(x(i)-b).^2/c.^2)+0.1*rand(1); 函数模型
% 在拟合数据的时候用的系数是
% a=1;
% b=4;
% c=10;
% 因此在拟合参数的时候,这里用 a=0.866
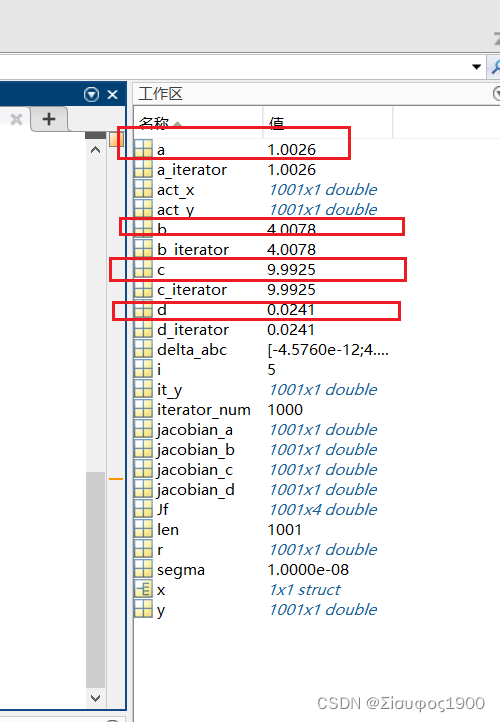
a=0.966;
b=3.98;
c=9.98;
d=0;
segma=0.00000001;
iterator_num=100;
x=load('x.mat');
act_x=x.x;
y=load('y.mat');
len=length(act_x);
jacobian_d=ones(len,1);
act_y=y.y;
plot(act_x,act_y,'.');
hold on;
for i=1:iterator_num
% 计算误差
y=a*exp(-(act_x-b).^2/c.^2)+d;
r=act_y-y;
% 开始计算偏导数矩阵
jacobian_a=exp(-(act_x - b).^2/c.^2);
jacobian_b=(a*exp(-(act_x - b).^2/c.^2).*(2.*act_x - 2*b))/c.^2;
jacobian_c=(2*a*exp(-(act_x - b).^2/c.^2).*(act_x - b).^2)/c.^3;
% jacobian_d
Jf=[jacobian_a,jacobian_b,jacobian_c,jacobian_d];
% H =Jf'*Jf
delta_abc=inv(Jf'*Jf)*Jf'*r;
% g=H*delta_abc 增量方程
a_iterator=a+delta_abc(1);
b_iterator=b+delta_abc(2);
c_iterator=c+delta_abc(3);
d_iterator=d+delta_abc(4);
% 判断精度
if norm(r)<segma
break;
end
a=a_iterator;
b=b_iterator;
c=c_iterator;
d=d_iterator;
end
it_y=a*exp(-(act_x-b).^2/c.^2)+d;
plot(act_x,it_y,'-');
legend('act','fit','Location','southoutside','Orientation','horizontal')