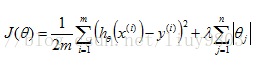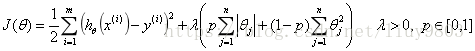一、欠拟合的解决方法
1、分析数据,增加特征维度;
2、增加多项式特征阶数;
3、减小正则项的超参系数值;
4、局部加权回归
二、过拟合的解决方法
1、分析数据,重新做数据清洗、特征工程;
2、扩充数据集,收集更多的数据;
3、减少特征数量,手动挑选保留哪些特征,调整模型选择算法;
4、采用正则化方法,保留所有特征,但减小θ的量级,适用于有很多特征且每一个特征都对模型预测有影响的情况
正则化(Regularization)
为了防止过拟合的情况出现,即θ的值不能过大,构造更简单(奥卡姆剃刀原理)、更平滑的预测函数,需要对损失函数加上一个惩罚项/正则项(一般对θ1, θ2,...,θn正则化,不对θ0正则化),正则项的形式有L1-norm,L2-norm,Elastic Net等。
范数(norm)是具有‘长度’概念的函数,用于衡量一个矢量的长度。
0范数:向量中非零元素的个数
1范数:向量中各元素绝对值之和
2范数:向量中各元素平方和再开根,即通常意义上的模
(1)Lasso回归(Least Absolute Shrinkage and Selection Operator)
使用L1正则的线性回归模型就称为Lasso回归。L1-norm(稀疏规则算子)通过稀疏模型化参数来降低模型的复杂度。
(2)岭回归(Ridge Regression)
使用L2正则的线性回归模型就称为岭回归。L2-norm通过缩小模型参数来防止过拟合的效果。与L1-norm不同,L2-norm不会让某些系数等于0,而是接近于0,且参数变小的过程加剧。
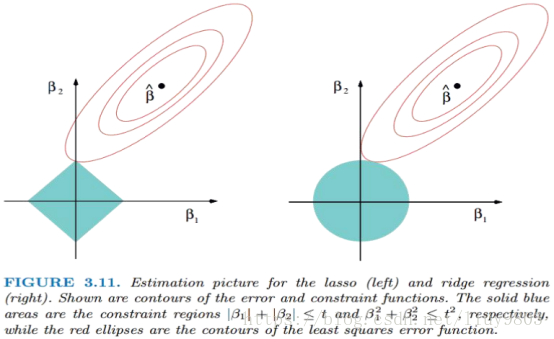
借用课件PPT,对L1-norm和L2-norm进行比较:
L2-norm中,由于对各个维度的参数缩放是在一个圆内进行的,处处可导,不太可能出现有维度参数变为0的情况,那么也就不会产生稀疏解。在实际应用中,数据是存在噪音和冗余的,稀疏解可以找到有用的维度并减少冗余,提高回归预测的准确性和鲁棒性,L1-norm可以达到最终解的稀疏性的要求。
Ridge回归模型具有较高的准确性、鲁棒性以及稳定性;Lasso回归模型具有较高的求解速度。
如果既要考虑稳定性也要考虑求解速度,就使用Elastic Net回归模型。
(3)Elastic Net
同时使用L1-norm和L2-norm的线性回归模型就称为弹性网络算法。
超参调节:
若正则参数λ过大,即对θ1,θ2,...,θn惩罚过大,则hθ(x)≈θ0接近一条直线,会导致欠拟合问题;若λ过小,又起不到正则作用。因此需要找到适合的参数λ。
方法:进行交叉验证GridSearhCV
Grid search网格搜索,即对网格中每个焦点进行遍历(穷举所有超参组合),从而找到最好的超参组合。缺点是组合数大的时候计算量很大。