1.理解LP问题的对偶变量含义
2.熟悉LP规划模型的定性和定量灵敏度分析
3.原问题与对偶问题是看同一个问题的不同视角
4.强对偶性是KKT条件成立是充分必要条件
5.掌握对偶单纯形法的详细流程,并体会与单纯形法的差异
线性规划(LP)是最基础的运筹优化模型,我们已经对它有了初步的认识,并学会了第一种求解方法——单纯形法。今天,我们进一步分析它,考虑模型结果对输入参数或常量变动的灵敏度。我们要用到一个新的案例(混料模型):
钢铁行业里,为了生产出满足各种化学成分要求的合金产品,金属废料需要加入一些纯添加剂来最大程度利用原材料。这是一个典型的混料问题。但由于添加剂极为昂贵,因此需要详细规划。而瑞典一家钢铁厂计划生产1000千克的熔炉进料,所有钢材的主要原材料是铁,下表列举了4种废料中碳、镍、铬、钼微量元素的含量比、可用数量以及单位成本(以瑞典货币克朗计量)。同时,表中也列出了3种可用的高成本纯添加剂以及最终混料中各种元素允许的含量范围。
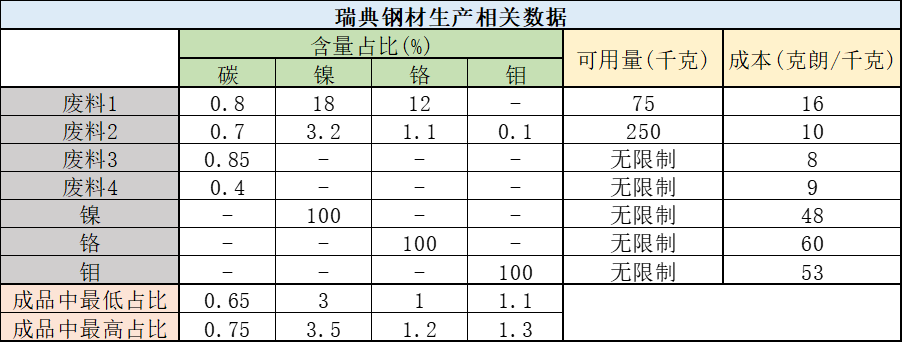
显然,该问题的具体模型为:

1
定性灵敏度分析
LP问题的灵敏度分析包括约束条件的系数和目标函数系数,前者又分为右端系数(RHS)和左端系数(LHS)。首先我们来考虑约束条件。
我们知道,约束条件可以分为松约束和紧约束。当放宽一个约束后,可行域增加了,对应的最优值只能不变或者更优,收紧一个约束后,最优值只能不变或更差。具体怎么评判系数变化对约束松紧的影响,我们要具体分析。我们利用上面的“瑞典钢铁厂”案例来加以说明。
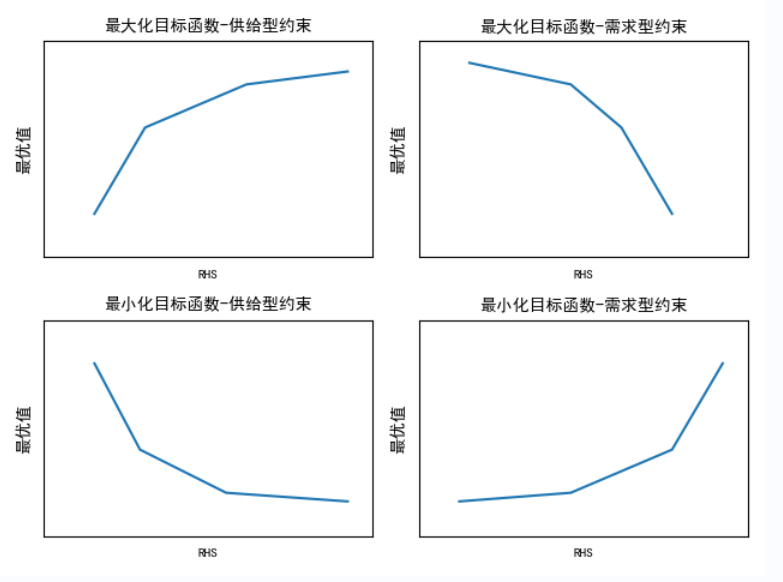
比如,假设其他参数不变,下图展示了改变废料1供给量限制的右端系数对目标最优值的影响:
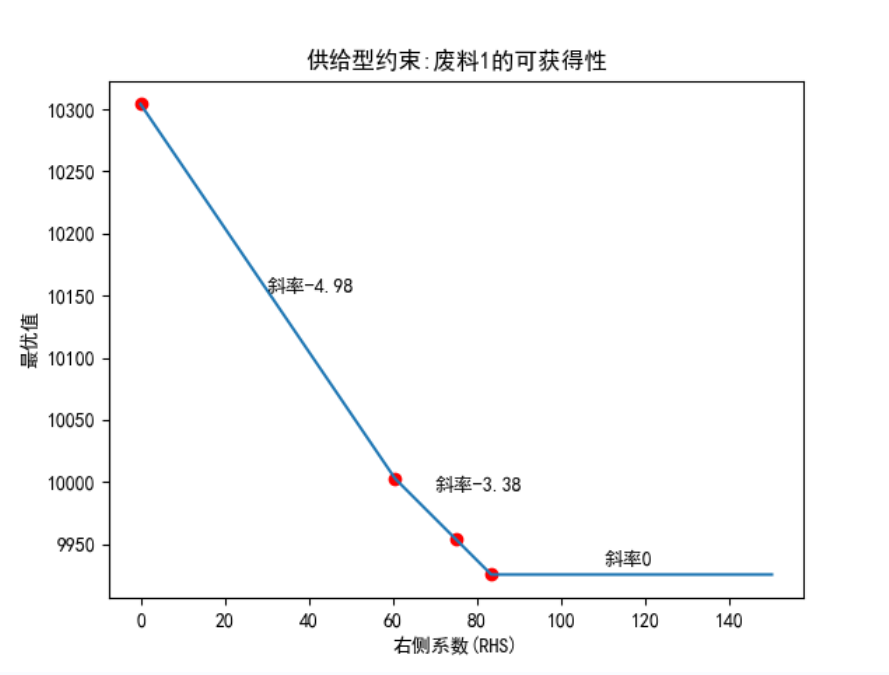
可以看到,随着右端系数的增加,碎片1的可行域范围变大,对应最小化目标函数,最优值先逐渐减少,但不是线性递减,在经过第二个红色的点(60.4,10003.023)后减少速率变慢,最后在第四个红点(83.3,9925.5185)后速率变为0.期间经过第三个红点(75,9953.6717),也即原来约束条件的右端系数。
我们在来看其他参数不变,改变铬最低限制对最优值的影响:
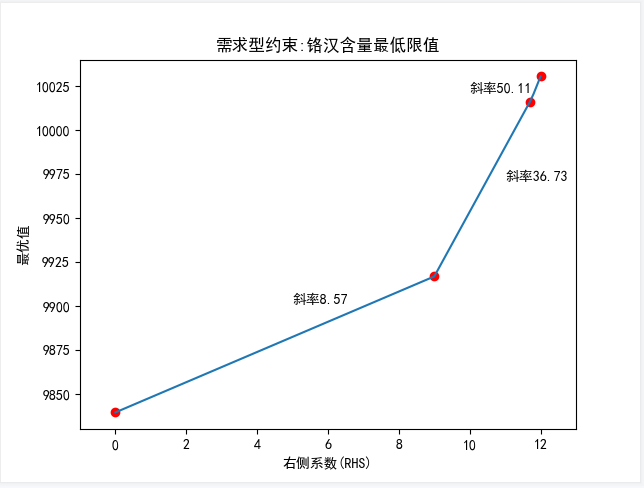
随着右端系数的增加,铬最低限制的可行域范围变小,对应最小化目标函数,最优值逐渐变大,但不是线性递增,在经过第二个红色的点(9,9916.944)后上升速率变快,最后在第三个红点(11.7,10016.108)后速率变得更大.最后在第四个红点(12,10030.472)速率变为无穷大(不可行)。
我们把类似这种“≤ ”的约束称为供给型约束,它的右端系数增加会放松约束,右端系数减少则收紧约束;把“≥” 的约束称为需求型约束,它的右端系数增加会收紧约束,右端系数减少则放松约束。
同理,左端系数变化也会对最优值有影响。假设其他参数不变,改变铬最低限制左端系数废料1的含量比对最优值的影响:
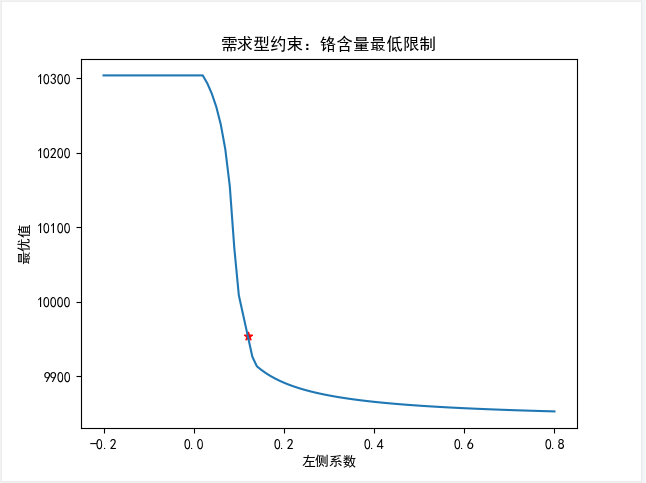
可以看到,左端系数变化对最优值的影响不再是线性的关系,五角星是原约束的系数0.12,如果增大系数,意味着更低废料1就能满足需求,约束成为松约束,最小化目标函数变得更优(减少),如果减少系数,意味着要更多的废料1才能满足需求,约束收紧,最小化目标函数不变或变差(增加).
对于供给型约束左端系数变化对目标值的影响,下图展示了镍含量最高限制左侧系数改变废料2含量比对最优值的变化:
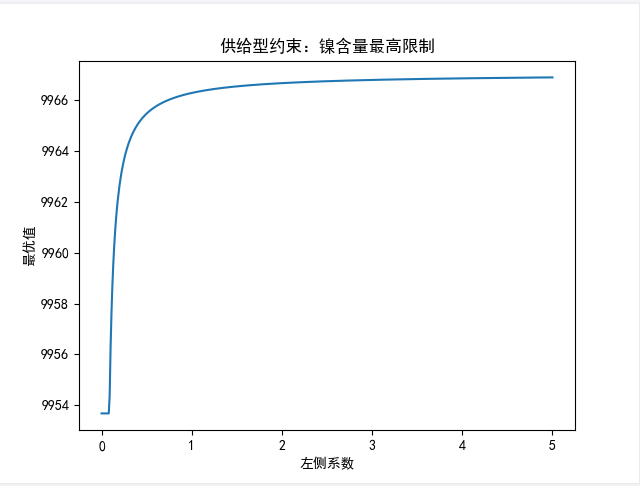
左端系数变化对最优值的影响不再是线性的关系,随着系数的增大,意味着满足供给型约束的废料2取值范围变小,约束收紧,最小化目标函数不变或变差(增加).
综上,我们得到:对于“≤ ”的供给型约束,它的左端系数增加会收紧约束,减少则放松约束;对于“≥” 的需求型约束,它的左端系数增加会放松约束,减少则收紧约束。
根据以上情况我们可以做一个推广,一个优化模型,增加一个约束条件可使得可行解集收紧,删去一个约束条件会使得可行解集放松。
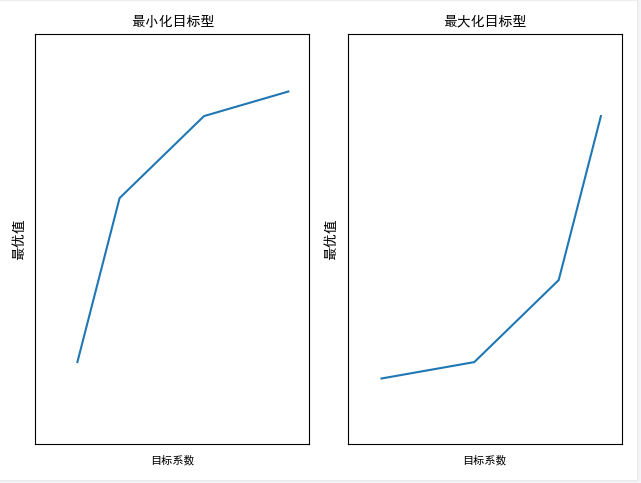
接下来我们看目标函数系数改变对最优值的影响。下图展示了废料4成本变化对最优值的影响:
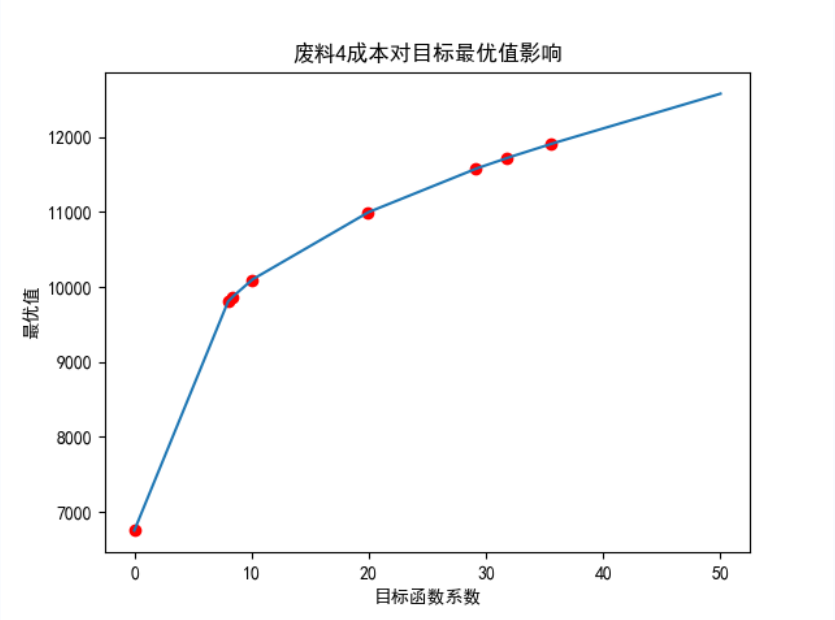
可以看到,随着成本的增加,呈现分段线性关系,最优值变差(增加)或不变,但速率越来越平缓。根据此,我们得到:改变一个非负变量的目标函数系数,系数增加使得最大化目标不变或更优,使得最小化目标不变或更差,系数减少使得最大化目标不变或更差,使得最小化目标不变或更优.
对于目标函数还要思考下面一个问题,增添或删减决策变量会对最优值有什么影响?比如瑞典钢铁生产模型,若增加一种废料,最优值就多了一种可能性,也就是最优值可能不变或者更优。因此,我们有:
优化模型中添加决策变量会使得最优值不变或更优,而删减决策变量使得最优值不变或变差!
最后,总结一下LP问题的定性灵敏度分析,列出了一下表格供参考:
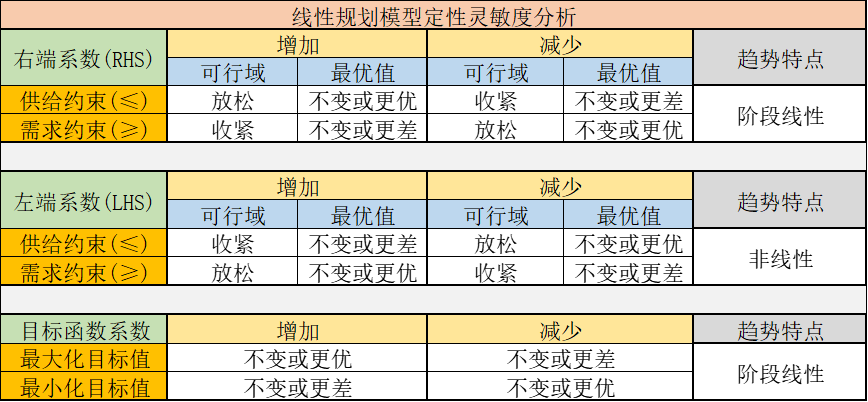
右端系数和目标函数系数变化引起最优值变化呈现阶段线性关系,我们可以用折线图表达出来,有助于我们对灵敏度分析有更感性的认识:
2
定量灵敏度分析
上一节定性灵敏度分析之研究了最优值变化的方向,我们要进一步分析其定量影响。首先引入对偶(dual)模型定义:
如果一个模型具有可以定量表示原始模型对系数变化的灵敏度的决策变量与约束条件,那么它就是该原始模型的对偶模型。原始(primal)模型就是最初给出的优化模型。
概念咋一看,比较晦涩难懂。我们需从更基本的概念入手理解——对偶变量(dual variable):每个原始问题的主约束都对应一个对偶变量,该变量的值对应这一主约束RHS系数每增加一个单位,原始问题最优值的变化量,通常把对偶变量记为v。
比如“瑞典钢铁厂”案例废料1的供给约束RHS系数,从图中我们可以知道,RHS=75时,对偶变量取值就是斜率:-3.38克朗/千克。更进一步,我们可以的得到所有RHS系数对应的对偶变量取值:

只要RHS落在一条折线的中间都很容易判断对偶变量取值,要是恰好落在两条线段的转折点上,这个定义就不清晰了,我们要借鉴左右极限的思想,来定义这种情况。比如RHS=60.42处,对偶变量的值可能是左侧线段的斜率-4.98或右侧的-3.38.
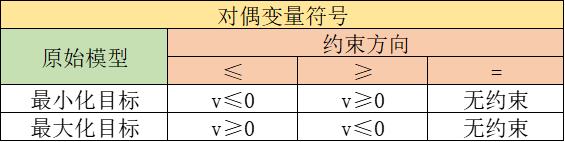
对偶变量表示RHS每增加一单位最优值的变化量,根据上一节的分析,它有以下的结论:
目标规划很多情况是关于成本最小化的场景,我们从经济学角度去看对偶变量,会变得非常容易理解——资源边际价格。举个例子,还记得“双原油”例子吗,我们引入对偶变量来表示该优化模型:

根据定义,v1表示为汽油需求量(RHS)增加一单位时目标成本的变化量,单位:千美元/千桶。它告诉我们一个隐含含义是:当RHS=2000桶时汽油的边际隐含价格,等价于在最优运作方案中,最后1000桶的成本。类似的,v4对应当前9000桶水平下沙特阿拉伯原油供给量变动的影响,也即1000桶额外的原油带来的隐含价值。
原模型的约束条件都是关于决策变量的,这些约束条件中非零系数可以被理解为单位生产活动消费(供给)或生产(需求)的资源量。那么这些系数与对应资源的隐含价格(对偶变量)v乘积之和,就是最小化问题的隐含价格或最大化问题的生产价值。

比如双原油案例中j=2表示委内瑞拉的生产活动,则每单位委内瑞拉原油的隐含价值为:
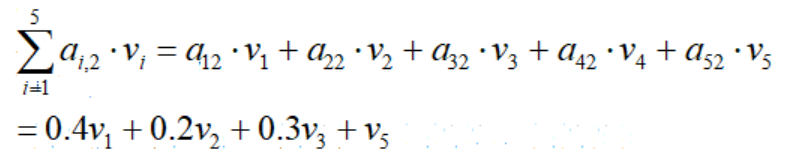
约束1~3是需求型约束,衡量单位委内瑞拉原油的贡献,最后一项是供给型约束,v5非正,表示资源的消耗量。这隐含价值表示了一单位委内瑞拉原油带来的收益。在最小化成本问题中,如果定价高于真实的成本,那么就高估了它的价值,但这样最优解会被改进。因此:
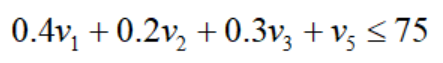
我们把这个称为主对偶约束,定义:

对偶变量表示每一个约束(需求或供给)的价格,RHS代表了需求量或供给量,整个对偶的资源价值为:

平衡点显然是该价值与原问题的最优值相等,因此有:

双原油的原始最优解与对偶问题最优解为:
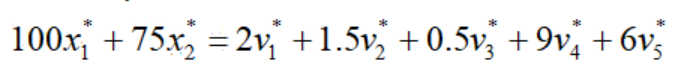
至此,我们把对偶模型介绍完毕,包括对偶变量、对偶变量约束(正负号)、主对偶约束、对偶变量目标函数。
这一节最后,我们还要介绍一个概念:互补松弛定理(primal complementary slackness)
如果在原始最优解情况下,一个约束是非积极约束,那么它对应的对偶变量为0
这一点非常容易理解,注意到我们对偶变量表示RHS变动一单位引起最优值的变化量,如果在最优解情况下,一个约束是非积极约束,表明不等号的等号不成立,那么RHS细微变动不会对最优值有任何影响,因此对偶变量取值必为0.
多数优化模型,主约束i的个数远远小于决策变量j的个数:i<j,因此,主对偶约束中,相对较少的对偶变量要满足过多的约束,这样就必定使得一些约束是非积极的,我们将最优值搜索限定到一个更小的范围内,这些限制条件是对偶互补松弛条件:
如果一个原始变量最优值不为0,那么对应的对偶变量使得对应的对偶约束是其作用的;如果对偶变量v使得对应的对偶约束是不起作用的,那么对应原始变量最优值为0
举个例子,对于下面的最小化目标规划问题,写出它的互补松弛条件和对偶互补松弛条件。

3
对偶性和KKT条件
有了前两节的铺垫,我们可以写出原始模型的对偶模型了。

举双原油的例子,它的对偶模型为:
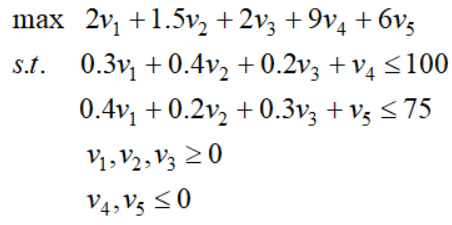
这里需要注意一点的是,上面两种情况都是基于原始变量非负的假设。我们要给出满足所有情况的对偶模型,下表展示了所有情况:
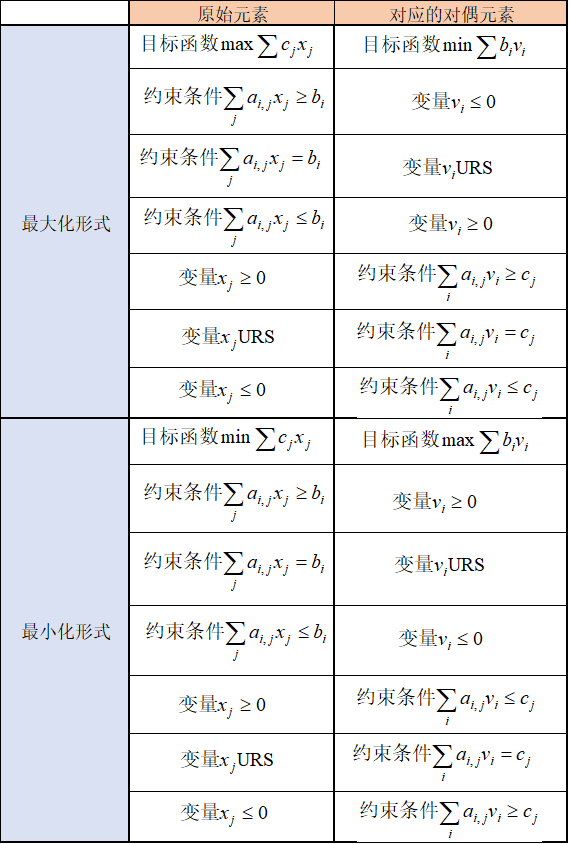
原问题和对偶问题是互为对偶的,也就是:一个LP的对偶问题的对偶是LP自身.
不失一般性,用一个统一简洁的形式表示原问题和对偶问题:
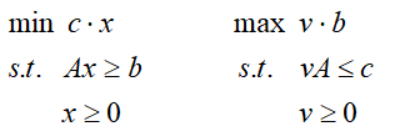
下面我们介绍弱对偶性:

弱对偶性表明,原问题的最优解大于等于对偶问题的最优解解。
进一步,如果不等号取等号,也即原问题的最优解等于对偶问题的最优解,我们称为强对偶性。此时,有以下结论:
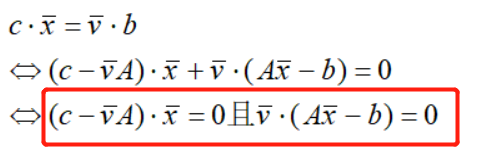
红色框称为松弛互补性。
强对偶性是建立在原问题和对偶问题有可行解的前提下,在此前提下加上松弛互补条件,我们统称为KKT条件:(1)原始问题有可行解(2)对偶问题有可行解(3)原问题与对偶问题具备松弛互补性
换句话说,KKT条件是满足强对偶性的充分必要条件!!!
举个例子来理解一下:

求解LP问题的单纯形法要求是标准的线性规划形式,因此有必要给出标准型LP问题的对偶问题以及KKT条件。这其实也很显然,直接列出:

4
对偶单纯形法
下面我们将单纯形法与对偶问题联系起来,假设B是包含当前基变量对应约束列的基子矩阵,N是当前非基变量对应约束列的子矩阵,则标准线性规划及其对偶形式为:
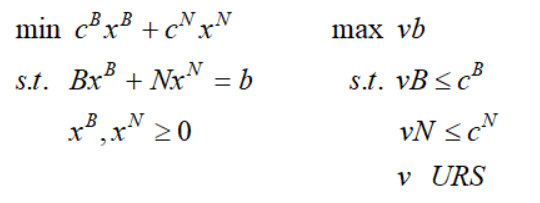
我们把这个称为分段的标准形式及分段的标准对偶形式,对应的KKT条件为:

由于非基变量固定为0,因此有以下结论:

注意看,红色框部分就是修正单纯形法中的定价向量,这个定价向量就是分段标准对偶形式的基本解。这样子只要这个基本解满足的对偶约束条件就是对偶可行解,我们有:

参考单纯形法思路,对于最小化标准形式的线性规划模型,我们可以给出对偶单纯形搜索算法:

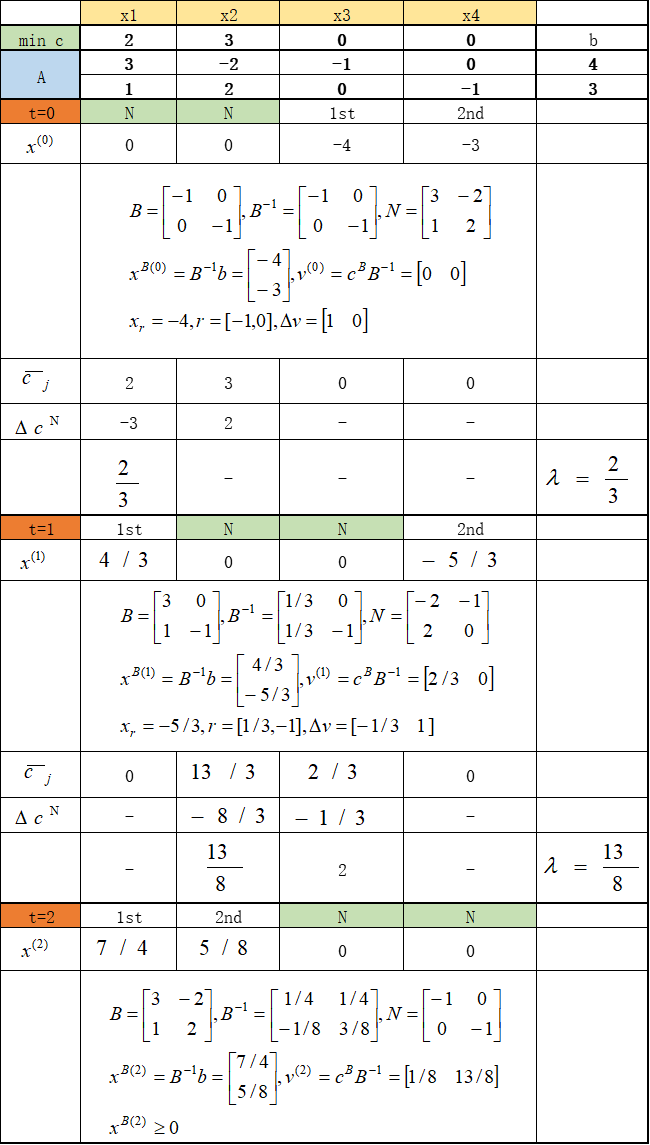
举个例子,对下面原始规划问题利用对偶单纯形法求解:
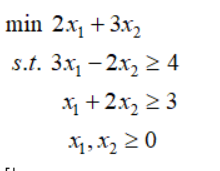
首先要引入松弛变量化成标准型,再利用算法求解,下表给出了详细的步骤: