浅谈三分法的原理及应用

最近简要地学习了三分法这一玄学操作，其实还是比较好理解的。只要多画画图就可以参透。

我们这里以一道经典的模板题来进行讲解：P3382 【模板】三分法

我们对于这种凸性函数求最值的问题，一般还是选择采用三分。

我们先来观察这种凸性函数（这里以上凸函数为例）

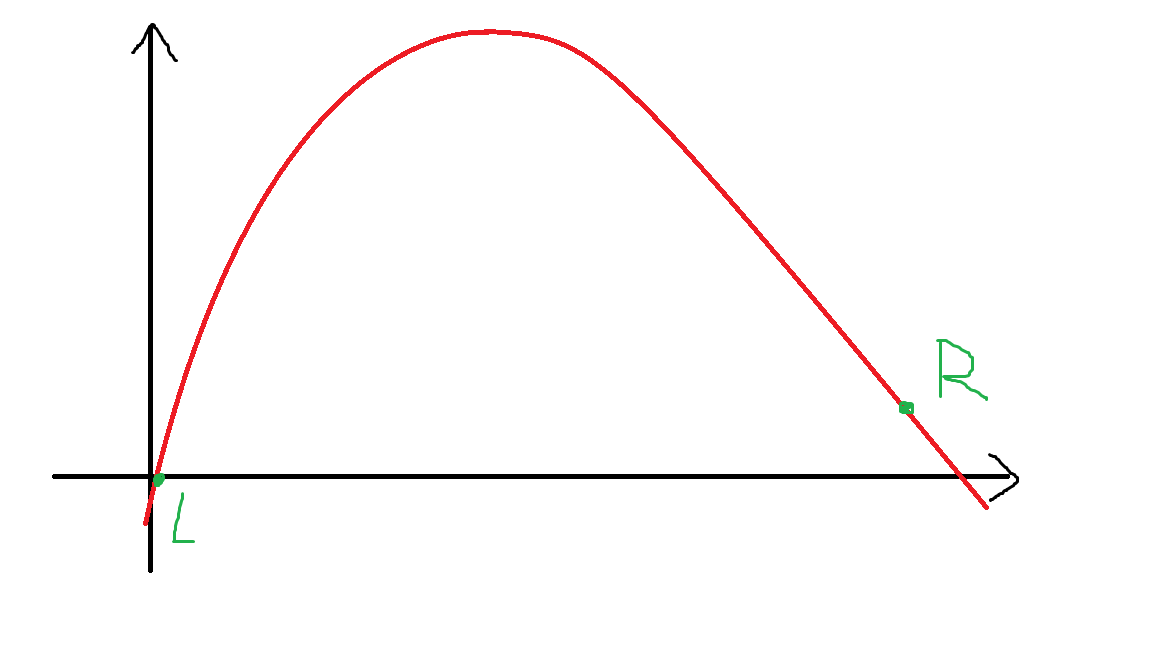
然后我们对于要求最大值的要求，发现如果使用传统的二分，那么很可能会直接经过最高点，所以我们使用三分。

我们取区间的三等分点，从左到右记作\(lmid\),\(rmid\)。

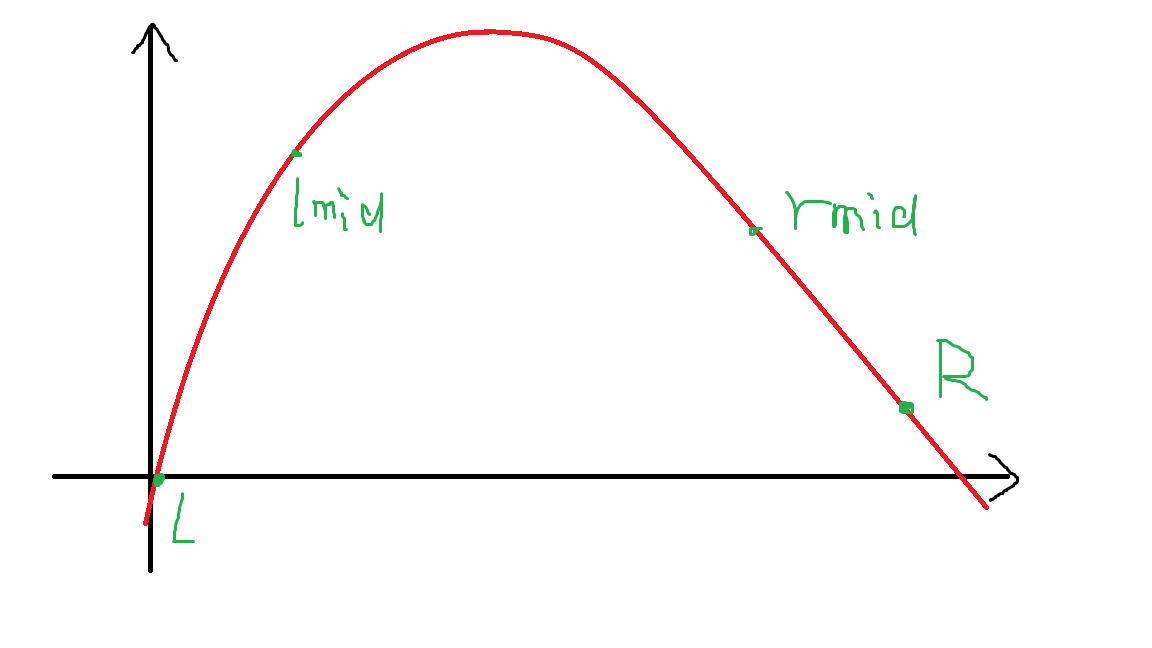
接下来我们对比一下\(f(lmid)\)与\(f(rmid)\)的值，若\(f(lmid)<f(rmid)\)那么区间就变为\(lmid\sim r\)否则变为\(l\sim rmid\)

证明的话也比较简单：

1. lmid与rmid在最值的同一侧。由于凸性函数在最大值（最小值）任意一侧都具有单调性，因此，lmid与rmid中，更大（小）的那个 数自然更为靠近最值。此时，我们远离最值的那个区间不可能包含最值，因此可以舍弃。

1. lmid与rmid在最值的两侧。由于最值在中间的一个区间，因此我们舍弃一个区间后，并不会影响到最值。

然后对于这一道板子题的话，我们对那个多次函数用秦九韶算法即可\(O(n)\)推导

扫描二维码关注公众号，回复： 1530714 查看本文章

CODE

#include<cstdio>
using namespace std;
typedef double DB;
const int N=15;
const DB EPS=1e-6;
int n;
DB a[N],l,r;
inline DB f(DB x)
{
    DB tot=0;
    for (register int i=n+1;i>=1;--i)
    tot=tot*x+a[n+2-i];
    return tot;
}
int main()
{
    register int i;
    scanf("%d%lf%lf",&n,&l,&r);
    for (i=1;i<=n+1;++i)
    scanf("%lf",&a[i]);
    while (r-l>EPS)
    {
        DB lmid=l+(r-l)/3.0,rmid=r-(r-l)/3.0;
        if (f(lmid)<f(rmid)) l=lmid; else r=rmid;
    }
    printf("%.5lf",l);
    return 0;
}

然后这里推荐一道比较好的题目：HDU3400Line belt