假设检验目录
- 一、假设检验的基本概念
- 二、正态总体参数的假设检验
-
- σ 2 已知,检验 μ 与 μ 0 的关系 \color{dodgerblue}\sigma^2\text{已知,检验}\mu\text{与}\mu_0\text{的关系} σ2已知,检验μ与μ0的关系
- σ 2 未知,检验 μ 与 μ 0 的关系 \color{dodgerblue}\sigma^2\text{未知,检验}\mu\text{与}\mu_0\text{的关系} σ2未知,检验μ与μ0的关系
- μ 已知,检验 σ 2 与 σ 0 2 的关系 \color{dodgerblue}\mu\text{已知,检验}\sigma^2\text{与}\sigma_0^2\text{的关系} μ已知,检验σ2与σ02的关系
- μ 未知,检验 σ 2 与 μ 0 的关系 \color{dodgerblue}\mu\text{未知,检验}\sigma^2\text{与}\mu_0\text{的关系} μ未知,检验σ2与μ0的关系
- σ 1 2 , σ 2 2 已知,检验 μ 1 − μ 2 与 Δ μ 的关系 \color{dodgerblue}\sigma_1^2,\sigma_2^2\text{已知,检验}\mu_1-\mu_2\text{与}\Delta\mu\text{的关系} σ12,σ22已知,检验μ1−μ2与Δμ的关系
- σ 1 2 = σ 2 2 未知,检验 μ 1 − μ 2 与 Δ μ 的关系 \color{dodgerblue}\sigma_1^2=\sigma_2^2\text{未知,检验}\mu_1-\mu_2\text{与}\Delta\mu\text{的关系} σ12=σ22未知,检验μ1−μ2与Δμ的关系
- μ 1 , μ 2 已知,检验 σ 1 2 σ 2 2 与 c 的关系 \color{dodgerblue}\mu_1,\mu_2\text{已知,检验}\frac{\sigma_1^2}{\sigma_2^2}\text{与}c\text{的关系} μ1,μ2已知,检验σ22σ12与c的关系
- μ 1 , μ 2 未知,检验 σ 1 2 σ 2 2 与 c 的关系 \color{dodgerblue}\mu_1,\mu_2\text{未知,检验}\frac{\sigma_1^2}{\sigma_2^2}\text{与}c\text{的关系} μ1,μ2未知,检验σ22σ12与c的关系
- 检验统计量的记忆方法 \color{limegreen}\text{检验统计量的记忆方法} 检验统计量的记忆方法
- 成对数据的假设检验 \textcolor{orchid}{\text{成对数据的假设检验}} 成对数据的假设检验
- 三、分布假设检验
一、假设检验的基本概念
假设检验:对总体提出某项假设→用样本检验假设
接受假设:认为假设正确
拒绝假设:认为假设错误
假设检验分为参数假设、分布假设
1. 假设检验的基本原理
实际推断原理:一个小概率事件在一次实验中是几乎不可能发生的
假设检验的思想:构造一个适用于检验假设 H 0 H_0 H0的统计量(检验统计量),若假设 H 0 H_0 H0成立则检验统计量满足一个条件(如果 H 0 H_0 H0成立则满足条件的概率很大),现在看样本满不满足这个条件,若满足则接受 H 0 H_0 H0,若不满足则拒绝 H 0 H_0 H0(这表明小概率事件发生了,原假设不成立,类似于拒取式推理)。
2. 两类错误
拒绝域 W W W:当检验统计量的观测值落在 W W W时,拒绝 H 0 H_0 H0
接受域 W ‾ \overline{W} W:当检验统计量的观测值落在 W ‾ \overline{W} W时,接受 H 0 H_0 H0
临界值:拒绝域和接受域的临界点
两类错误:
第I类错误: H 0 H_0 H0为真但被拒绝了
第II类错误: H 0 H_0 H0为假但被接受了
显著性水平 α \alpha α:犯第I类错误的概率, P { 拒绝 H 0 ∣ H 0 为真 } = α P\{\text{拒绝}H_0|H_0\text{为真}\}=\alpha P{
拒绝H0∣H0为真}=α,反映了拒绝 H 0 H_0 H0的说服力
β \beta β:犯第II类错误的概率, P { 接受 H 0 ∣ H 0 不真 } = β P\{\text{接受}H_0|H_0\text{不真}\}=\beta P{
接受H0∣H0不真}=β
在样本容量 n n n一定的情况下, α \alpha α减小, β \beta β就会增大
显著性检验:控制犯第I类错误的概率不超过一个值(显著性水平),不考虑第II类错误
显著性水平为 α \alpha α的检验法:犯第I类错误的概率不超过 α \alpha α,即 P { 拒绝 H 0 ∣ H 0 为真 } ≤ α P\{\text{拒绝}H_0|H_0\text{为真}\}\le\alpha P{
拒绝H0∣H0为真}≤α
在所有显著性水平为 α \alpha α的检验法中,犯第II类错误的概率 β \beta β最小的检验法为最好的检验法
3. 假设检验的一般步骤
(1) 充分考虑和利用已知的背景知识提出原假设 H 0 H_0 H0即备择假设 H 1 H_1 H1。
H 1 H_1 H1是 H 0 H_0 H0的对立面,称为对立假设或备择假设。 H 0 H_0 H0一般是“要保护的假设”或“维持现状的假设”,错误拒绝假设 H 0 H_0 H0比错误拒绝假设 H 1 H_1 H1带来更严重的后果。实践中, H 0 H_0 H0不应被轻易否定,若否定必须要有充分的理由。
(2) 确定检验统计量 Z Z Z,并在 H 0 H_0 H0成立的前提下导出 Z Z Z的概率分布,要求 Z Z Z的分布不依赖于任何未知参数。
这里的 Z Z Z与参数估计中的枢轴量类似,选取 Z Z Z的原因都是为了排除未知参数的干扰,用一个确定的分布求出拒绝域。
(3) 确定拒绝域。依据直观分析先确定拒绝域的形式,然后根据给定的水平 α \alpha α和 Z Z Z的分布,由 P { 拒绝 H 0 ∣ H 0 为真 } = α P\{\text{拒绝}H_0|H_0\text{为真}\}=\alpha P{ 拒绝H0∣H0为真}=α确定拒绝域的临界值,从而确定拒绝域。
确定拒绝域与参数估计中确定置信区间的过程类似。
(4) 作一次具体的抽样,根据得到的样本值和上面确定的拒绝域对 H 0 H_0 H0作出拒绝或接受的判断。
如果 Z Z Z的观测值落入拒绝域 W W W,则拒绝原假设 H 0 H_0 H0,接受备择假设 H 1 H_1 H1;若落入接受域 W ‾ \overline{W} W,则接受原假设 H 0 H_0 H0,拒绝备择假设 H 1 H_1 H1。
Z ∈ W ‾ ⟶ H 0 H 1 Z ∈ W ⟶ H 1 H 0 Z\in\overline{W}\longrightarrow \textcolor{green}{H_0}\,\textcolor{red}{\sout{H_1}}\\ Z\in W\longrightarrow \textcolor{green}{H_1}\,\textcolor{red}{\sout{H_0}} Z∈W⟶H0H1Z∈W⟶H1H0
4. p p p值
p p p值:利用样本值的拒绝原假设的最小显著性水平称为 p p p值。
α < p ⟶ H 0 H 1 = Z 落入 接受域 内 α ≥ p ⟶ H 1 H 0 = Z 落入 拒绝域 内 \alpha<p\longrightarrow \textcolor{green}{H_0}\,\textcolor{red}{\sout{H_1}}\;=Z\text{落入\textcolor{green}{接受域}内}\\ \alpha\ge p\longrightarrow \textcolor{green}{H_1}\,\textcolor{red}{\sout{H_0}}\;=Z\text{落入\textcolor{red}{拒绝域}内} α<p⟶H0H1=Z落入接受域内α≥p⟶H1H0=Z落入拒绝域内 p p p值是“拒绝”的最小显著性水平,也就是说如果 α \alpha α大于等于 p p p,那就拒绝。直观地讲, α \alpha α越小,越不容易拒绝原假设 H 0 H_0 H0,拒绝 H 0 H_0 H0就越有说服力; α \alpha α越小,拒绝域也就越“小”。
在固定 α \alpha α的情况下, p p p越大,越容易接受 H 0 H_0 H0(简称“ p p p越大越好”)。

我感觉, α \alpha α是一种对拒绝 H 0 H_0 H0的“容忍度”,也就是对 H 0 H_0 H0的“怀疑程度”; α \alpha α越小,对 H 0 H_0 H0的怀疑程度越小,越容易接受 H 0 H_0 H0。 p p p值是对 H 0 H_0 H0的最小“怀疑程度”,如果 α < p \alpha<p α<p,那么这个 α \alpha α比 p p p对 H 0 H_0 H0“更有信心”,所以接受 H 0 H_0 H0。总结起来,就是: α \alpha α越小,对 H 0 H_0 H0越有信心。
用拒绝域判断的方法称为临界值法,用 p p p值的叫做 p p p值法。
二、正态总体参数的假设检验
检验统计量服从正态分布 → u \;\to u →u检验法
检验统计量服从 χ 2 \chi^2 χ2分布 → χ 2 \;\to \chi^2 →χ2检验法
检验统计量服从 t t t分布 → t \;\to t →t检验法
检验统计量服从 F F F分布 → F \;\to F →F检验法
对于单个总体的情形,我们设 X ~ N ( μ , σ 2 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}X\td N(\mu,\sigma^2) X~N(μ,σ2);对于两个总体的情形,我们设 X ~ N ( μ 1 , σ 1 2 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}X\td N(\mu_1,\sigma_1^2) X~N(μ1,σ12), Y ~ N ( μ 2 , σ 2 2 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}Y\td N(\mu_2,\sigma_2^2) Y~N(μ2,σ22)。 X X X的样本容量为 n n n,样本方差为 S X 2 S_X^2 SX2; Y Y Y的样本容量为 m m m,样本方差为 S Y 2 S_Y^2 SY2。
下面是单个总体的情形( X ~ N ( μ , σ 2 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}X\td N(\mu,\sigma^2) X~N(μ,σ2))。
σ 2 已知,检验 μ 与 μ 0 的关系 \color{dodgerblue}\sigma^2\text{已知,检验}\mu\text{与}\mu_0\text{的关系} σ2已知,检验μ与μ0的关系
双侧假设检验:提出假设: H 0 : μ = μ 0 H 1 : μ ≠ μ 0 \begin{aligned} &\textcolor{green}{H_0:\mu=\mu_0}&\\ &\textcolor{red}{H_1:\mu\ne\mu_0}& \end{aligned} H0:μ=μ0H1:μ=μ0回顾一下 α \alpha α是犯第一类错误的概率,即当 H 0 H_0 H0成立时 P { 拒绝 H 0 } = α P\{\text{拒绝}H_0\}=\alpha P{ 拒绝H0}=α。因为只有假设 H 0 H_0 H0成立我们才能继续分析,所以我们必须令 H 0 H_0 H0先成立,即 μ = μ 0 \mu=\mu_0 μ=μ0成立。此时 X ~ N ( μ 0 , σ 2 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}X\td N(\mu_0,\sigma^2) X~N(μ0,σ2),我们给出检验统计量 U = n ( X ‾ − μ 0 ) σ ~ N ( 0 , 1 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}U=\cfrac{\sqrt{n}\left(\overline{X}-\mu_0\right)}{\sigma}\td N(0,1) U=σn(X−μ0)~N(0,1)。 H 0 H_0 H0什么时候成立呢?就是样本均值 X ‾ \overline{X} X与 μ 0 \mu_0 μ0比较接近的时候成立,太离谱了就拒绝。现在我们已经假定 H 0 H_0 H0成立了,只要保证 U U U的观测值落入拒绝域的概率为 α \alpha α就可以了。这和区间估计类似,因为 P { U ≥ u α / 2 或 U ≤ − u α / 2 } = α P\{U\ge u_{\alpha/2}\text{或}U\le-u_{\alpha/2}\}=\alpha P{ U≥uα/2或U≤−uα/2}=α,所以拒绝的时候就是 ∣ U ∣ ≥ u α / 2 |U|\ge u_{\alpha/2} ∣U∣≥uα/2的时候。对于确定的样本,我们算出样本的 U U U值,然后判断 ∣ U ∣ |U| ∣U∣和 u α / 2 u_{\alpha/2} uα/2的关系就可以了。如果 ∣ U ∣ ≥ u α / 2 |U|\ge u_{\alpha/2} ∣U∣≥uα/2,那么也就说在 H 0 H_0 H0成立的条件下一个概率仅仅只有 α \alpha α的事件发生了,这说明 H 0 H_0 H0不太可能成立,所以我们拒绝 H 0 H_0 H0。注意, U U U衡量的是 X ‾ \overline{X} X与 μ \mu μ的差异,差异太大就拒绝 H 0 H_0 H0; U U U中除以 σ \sigma σ的目的是去除量纲,进行标准化。
单侧假设检验:提出假设: H 0 : μ = μ 0 H 1 : μ ≥ μ 0 \begin{aligned} &\textcolor{green}{H_0:\mu=\mu_0}&\\ &\textcolor{red}{H_1:\mu\ge\mu_0}& \end{aligned} H0:μ=μ0H1:μ≥μ0因为均值 μ \mu μ不会小于 μ 0 \mu_0 μ0,所以 U ≤ − u α / 2 U\le -u_{\alpha/2} U≤−uα/2的拒绝域就不存在了,只剩下 U ≥ 某个值 U\ge\text{某个值} U≥某个值的拒绝域。这个值是多少呢?不要忘了, U U U落入拒绝域的概率是 α \alpha α,所以显然这个值是 u α u_{\alpha} uα,拒绝域为 U ≥ u α U\ge u_{\alpha} U≥uα。把 H 0 \textcolor{green}{H_0} H0改成 H 0 : μ ≤ μ 0 \textcolor{green}{H_0:\mu\le\mu_0} H0:μ≤μ0,拒绝域还是一样的。
σ 2 未知,检验 μ 与 μ 0 的关系 \color{dodgerblue}\sigma^2\text{未知,检验}\mu\text{与}\mu_0\text{的关系} σ2未知,检验μ与μ0的关系
检验统计量 T = n ( X ‾ − μ 0 ) S ~ t ( n − 1 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}T=\cfrac{\sqrt{n}\left(\overline{X}-\mu_0\right)}{S}\td t(n-1) T=Sn(X−μ0)~t(n−1)
拒绝域与 σ 2 \sigma^2 σ2已知时类似,就是把 u α u_{\alpha} uα换成了 t α ( n − 1 ) t_{\alpha}(n-1) tα(n−1)而已。
μ 已知,检验 σ 2 与 σ 0 2 的关系 \color{dodgerblue}\mu\text{已知,检验}\sigma^2\text{与}\sigma_0^2\text{的关系} μ已知,检验σ2与σ02的关系
检验统计量 χ 2 = ∑ i = 1 n ( X i − μ ) 2 σ 0 2 ~ χ 2 ( n ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}\chi^2=\cfrac{\sum\limits_{i=1}^n{\left(X_i-\mu\right)}^2}{\sigma_0^2}\td\chi^2(n) χ2=σ02i=1∑n(Xi−μ)2~χ2(n)
μ 未知,检验 σ 2 与 μ 0 的关系 \color{dodgerblue}\mu\text{未知,检验}\sigma^2\text{与}\mu_0\text{的关系} μ未知,检验σ2与μ0的关系
检验统计量 χ 2 = ∑ i = 1 n ( X i − X ‾ ) 2 σ 0 2 = ( n − 1 ) S 2 σ 0 2 ~ χ 2 ( n − 1 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}\chi^2=\cfrac{\sum\limits_{i=1}^n{\left(X_i-\overline{X}\right)}^2}{\sigma_0^2}=\cfrac{(n-1)S^2}{\sigma_0^2}\td\chi^2(n-1) χ2=σ02i=1∑n(Xi−X)2=σ02(n−1)S2~χ2(n−1)
双侧假设检验 H 0 : σ 2 = σ 0 2 , H 1 : σ 2 ≠ μ 0 2 \textcolor{green}{H_0:\sigma^2=\sigma_0^2},\textcolor{red}{H_1:\sigma^2\ne\mu_0^2} H0:σ2=σ02,H1:σ2=μ02的拒绝域为 { χ 2 ≤ χ 1 − α / 2 2 ( n − 1 ) } ⋃ { χ 2 ≥ χ α / 2 2 ( n − 1 ) } \textcolor{chocolate}{\left\{\chi^2\le\chi^2_{1-\alpha/2}(n-1)\right\}\bigcup\left\{\chi^2\ge\chi^2_{\alpha/2}(n-1)\right\}} {
χ2≤χ1−α/22(n−1)}⋃{
χ2≥χα/22(n−1)}。
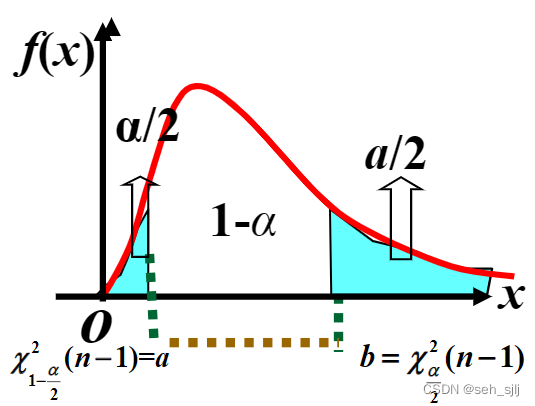
单侧假设检验 H 0 : σ 2 = σ 0 2 , H 1 : σ 2 > σ 0 2 \textcolor{green}{H_0:\sigma^2=\sigma_0^2},\textcolor{red}{H_1:\sigma^2>\sigma_0^2} H0:σ2=σ02,H1:σ2>σ02的拒绝域为 χ 2 ≥ χ α 2 ( n − 1 ) \chi^2\ge\chi^2_\alpha(n-1) χ2≥χα2(n−1)。
单侧假设检验 H 0 : σ 2 = σ 0 2 , H 1 : σ 2 < σ 0 2 \textcolor{green}{H_0:\sigma^2=\sigma_0^2},\textcolor{red}{H_1:\sigma^2<\sigma_0^2} H0:σ2=σ02,H1:σ2<σ02的拒绝域为 χ 2 ≤ χ 1 − α 2 ( n − 1 ) \chi^2\le\chi^2_{1-\alpha}(n-1) χ2≤χ1−α2(n−1)。
σ 1 2 , σ 2 2 已知,检验 μ 1 − μ 2 与 Δ μ 的关系 \color{dodgerblue}\sigma_1^2,\sigma_2^2\text{已知,检验}\mu_1-\mu_2\text{与}\Delta\mu\text{的关系} σ12,σ22已知,检验μ1−μ2与Δμ的关系
检验统计量 U = ( X ‾ − Y ‾ ) − Δ μ σ 1 2 n + σ 2 2 m ~ N ( 0 , 1 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}U=\cfrac{\left(\overline{X}-\overline{Y}\right)-\Delta\mu}{\sqrt{\frac{\sigma_1^2}{n}+\frac{\sigma_2^2}{m}}}\td N(0,1) U=nσ12+mσ22(X−Y)−Δμ~N(0,1)
σ 1 2 = σ 2 2 未知,检验 μ 1 − μ 2 与 Δ μ 的关系 \color{dodgerblue}\sigma_1^2=\sigma_2^2\text{未知,检验}\mu_1-\mu_2\text{与}\Delta\mu\text{的关系} σ12=σ22未知,检验μ1−μ2与Δμ的关系
检验统计量 T = ( X ‾ − Y ‾ ) − Δ μ S W 1 n + 1 m ~ t ( n + m − 2 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}T=\cfrac{\left(\overline{X}-\overline{Y}\right)-\Delta\mu}{S_W\sqrt{\frac{1}{n}+\frac{1}{m}}}\td t(n+m-2) T=SWn1+m1(X−Y)−Δμ~t(n+m−2),其中 S W = ( n − 1 ) S X 2 + ( m − 1 ) S Y 2 n + m − 2 S_W=\sqrt{\cfrac{(n-1)S_X^2+(m-1)S_Y^2}{n+m-2}} SW=n+m−2(n−1)SX2+(m−1)SY2
μ 1 , μ 2 已知,检验 σ 1 2 σ 2 2 与 c 的关系 \color{dodgerblue}\mu_1,\mu_2\text{已知,检验}\frac{\sigma_1^2}{\sigma_2^2}\text{与}c\text{的关系} μ1,μ2已知,检验σ22σ12与c的关系
检验统计量 F = ∑ i = 1 n ( X i − μ 1 ) 2 n ∑ j = 1 m ( Y j − μ 2 ) 2 m / c = 1 c m ∑ i = 1 n ( X i − μ 1 ) 2 n ∑ j = 1 m ( Y j − μ 2 ) 2 ~ F ( n , m ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}F=\left.\cfrac{\sum\limits_{i=1}^n\cfrac{ {(X_i-\mu_1)}^2}{n}}{\sum\limits_{j=1}^m\cfrac{ {(Y_j-\mu_2)}^2}{m}}\right/c=\cfrac{1}{c}\cfrac{m\sum\limits_{i=1}^n{(X_i-\mu_1)}^2}{n\sum\limits_{j=1}^m{(Y_j-\mu_2)}^2}\td F(n,m) F=j=1∑mm(Yj−μ2)2i=1∑nn(Xi−μ1)2/c=c1nj=1∑m(Yj−μ2)2mi=1∑n(Xi−μ1)2~F(n,m)
μ 1 , μ 2 未知,检验 σ 1 2 σ 2 2 与 c 的关系 \color{dodgerblue}\mu_1,\mu_2\text{未知,检验}\frac{\sigma_1^2}{\sigma_2^2}\text{与}c\text{的关系} μ1,μ2未知,检验σ22σ12与c的关系
检验统计量 F = 1 c S X 2 S Y 2 ~ F ( n − 1 , m − 1 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}F=\cfrac{1}{c}\cfrac{S_X^2}{S_Y^2}\td F(n-1,m-1) F=c1SY2SX2~F(n−1,m−1)
注意 F 1 − α ( n , m ) = 1 F α ( m , n ) F_{1-\alpha}(n,m)=\cfrac{1}{F_{\alpha}(m,n)} F1−α(n,m)=Fα(m,n)1(要干三件事情:①取倒数、② 1 − α 1-\alpha 1−α变 α \alpha α、③交换 n , m n,m n,m的次序)。拒绝域与 χ 2 \chi^2 χ2检验类似。
检验统计量的记忆方法 \color{limegreen}\text{检验统计量的记忆方法} 检验统计量的记忆方法
-
单个变量检验均值:为了把分布标准化,我们需要排除三个因素的影响:均值( μ \mu μ)、样本容量( n n n)、标准差( σ \sigma σ或 S S S),其中排除标准差也是使数据无量纲化。所以,分别对应标准差已知与未知,我们有统计量 U = n ( X ‾ − μ ) σ U=\cfrac{\sqrt{n}\left(\overline{X}-\mu\right)}{\sigma} U=σn(X−μ)和 T = n ( X ‾ − μ ) S T=\cfrac{\sqrt{n}\left(\overline{X}-\mu\right)}{S} T=Sn(X−μ),前者服从 N ( 0 , 1 ) N(0,1) N(0,1),后者服从 t ( n − 1 ) t(n-1) t(n−1)。
-
单个变量检验方差:我们的统计量应该服从卡方分布,注意 χ 2 ( n ) \chi^2(n) χ2(n)的期望是 n n n,所以我们要求当知道均值时我们的统计量的期望应该是 n n n,不知道均值时为 n − 1 n-1 n−1。注意 E [ ∑ i = 1 n ( X i − μ ) 2 ] = n E [ ( X 1 − μ ) 2 ] E\left[\sum\limits_{i=1}^n{\left(X_i-\mu\right)}^2\right]=nE\left[{\left(X_1-\mu\right)}^2\right] E[i=1∑n(Xi−μ)2]=nE[(X1−μ)2],而 μ = E ( X 1 ) \mu=E(X_1) μ=E(X1),所以根据方差的定义有 E [ ( X 1 − μ ) 2 ] = σ 2 E\left[{\left(X_1-\mu\right)}^2\right]=\sigma^2 E[(X1−μ)2]=σ2,因此 E [ ∑ i = 1 n ( X i − μ ) 2 ] = n σ 2 E\left[\sum\limits_{i=1}^n{\left(X_i-\mu\right)}^2\right]=n\sigma^2 E[i=1∑n(Xi−μ)2]=nσ2。同时我们知道, E ( S 2 ) = σ 2 E\left(S^2\right)=\sigma^2 E(S2)=σ2,即 E [ ∑ i = 1 n ( X i − X ‾ ) 2 ] = ( n − 1 ) σ 2 E\left[\sum\limits_{i=1}^n{\left(X_i-\overline{X}\right)}^2\right]=(n-1)\sigma^2 E[i=1∑n(Xi−X)2]=(n−1)σ2。因此,我们采用的两个检验统计量分别为 ∑ i = 1 n ( X i − μ ) 2 σ 2 \cfrac{\sum\limits_{i=1}^n{\left(X_i-\mu\right)}^2}{\sigma^2} σ2i=1∑n(Xi−μ)2和 ∑ i = 1 n ( X i − μ ) 2 σ 2 \cfrac{\sum\limits_{i=1}^n{\left(X_i-\mu\right)}^2}{\sigma^2} σ2i=1∑n(Xi−μ)2,分别服从自由度为 n n n和 n − 1 n-1 n−1的卡方分布。可以理解为:在我们用到的检验统计量中,量纲是平方且期望是 n n n的就服从 χ 2 ( n ) \chi^2(n) χ2(n)。
-
两个变量检验均值差:注意 X ‾ − Y ‾ ~ N ( μ 1 − μ 2 , σ 1 2 n + σ 2 2 m ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}\overline{X}-\overline{Y}\td N\left(\mu_1-\mu_2,\frac{\sigma_1^2}{n}+\frac{\sigma_2^2}{m}\right) X−Y~N(μ1−μ2,nσ12+mσ22)。模仿单个变量检验均值时的情形,方差已知的情况这里不再赘述;对于方差未知的情况,要求 σ 1 2 = σ 2 2 \sigma_1^2=\sigma_2^2 σ12=σ22,为方便起见我们都记为 σ 2 \sigma^2 σ2。此时 D ( X ‾ − Y ‾ ) = σ 2 ( 1 n + 1 m ) D\left(\overline{X}-\overline{Y}\right)=\sigma^2\left(\frac{1}{n}+\frac{1}{m}\right) D(X−Y)=σ2(n1+m1),所用的检验统计量应为 ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 n + 1 m \cfrac{\left(\overline{X}-\overline{Y}\right)-(\mu_1-\mu_2)}{\sigma\sqrt{\frac{1}{n}+\frac{1}{m}}} σn1+m1(X−Y)−(μ1−μ2),但 σ \sigma σ未知,所以我们必须把 σ \sigma σ替换为一个用 S X S_X SX和 S Y S_Y SY表示的估计值。怎么估计呢?我们设估计 σ 2 \sigma^2 σ2的量是 S W 2 S_W^2 SW2。首先,这个 S W 2 S_W^2 SW2的期望必须是 σ 2 \sigma^2 σ2;其次,它除以 σ 2 \sigma^2 σ2以后必须服从 χ 2 ( n + m − 2 ) \chi^2(n+m-2) χ2(n+m−2)(要求自由度是满的)。我们想想, ∑ i = 1 n ( X i − X ‾ ) 2 + ∑ j = 1 m ( Y j − Y ‾ ) 2 \sum\limits_{i=1}^n{\left(X_i-\overline{X}\right)}^2+\sum\limits_{j=1}^m{\left(Y_j-\overline{Y}\right)}^2 i=1∑n(Xi−X)2+j=1∑m(Yj−Y)2是什么呢?它其实就是 ( n − 1 ) S X 2 + ( m − 1 ) S Y 2 (n-1)S_X^2+(m-1)S_Y^2 (n−1)SX2+(m−1)SY2,而且 ( n − 1 ) S X 2 + ( m − 1 ) S Y 2 σ 2 ~ χ 2 ( n + m − 2 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}\cfrac{(n-1)S_X^2+(m-1)S_Y^2}{\sigma^2}\td \chi^2(n+m-2) σ2(n−1)SX2+(m−1)SY2~χ2(n+m−2), E ( ( n − 1 ) S X 2 + ( m − 1 ) S Y 2 n + m − 2 ) = σ 2 E\left(\cfrac{(n-1)S_X^2+(m-1)S_Y^2}{n+m-2}\right)=\sigma^2 E(n+m−2(n−1)SX2+(m−1)SY2)=σ2。所以,我们就用 S W = ( n − 1 ) S X 2 + ( m − 1 ) S Y 2 n + m − 2 S_W=\sqrt{\cfrac{(n-1)S_X^2+(m-1)S_Y^2}{n+m-2}} SW=n+m−2(n−1)SX2+(m−1)SY2来替换检验统计量中的 σ \sigma σ,得到 T = ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) S W 1 n + 1 m T=\cfrac{\left(\overline{X}-\overline{Y}\right)-(\mu_1-\mu_2)}{S_W\sqrt{\frac{1}{n}+\frac{1}{m}}} T=SWn1+m1(X−Y)−(μ1−μ2)。
-
两个变量检验方差比:其实检验统计量就是一个 测得的方差比 要求的方差比 \cfrac{\text{测得的方差比}}{\text{要求的方差比}} 要求的方差比测得的方差比的形式。还有一种理解方式:我们知道 χ X 2 = ( n − 1 ) S X 2 σ 1 2 ~ χ 2 ( n − 1 ) \chi^2_X=\newcommand{\td}{\,\text{\large\textasciitilde}\,}\cfrac{(n-1)S_X^2}{\sigma_1^2}\td\chi^2(n-1) χX2=σ12(n−1)SX2~χ2(n−1), χ Y 2 = ( m − 1 ) S Y 2 σ 2 2 ~ χ 2 ( m − 1 ) \chi^2_Y=\newcommand{\td}{\,\text{\large\textasciitilde}\,}\cfrac{(m-1)S_Y^2}{\sigma_2^2}\td\chi^2(m-1) χY2=σ22(m−1)SY2~χ2(m−1),根据 F F F分布的性质我们知道 χ X 2 / ( n − 1 ) χ Y 2 / ( m − 1 ) ~ F ( n − 1 , m − 1 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}\cfrac{\chi^2_X/(n-1)}{\chi^2_Y/(m-1)}\td F(n-1,m-1) χY2/(m−1)χX2/(n−1)~F(n−1,m−1),也就是 S X 2 / σ 1 2 S Y 2 / σ 2 2 ~ F ( n − 1 , m − 1 ) \newcommand{\td}{\,\text{\large\textasciitilde}\,}\cfrac{S_X^2/\sigma_1^2}{S_Y^2/\sigma_2^2}\td F(n-1,m-1) SY2/σ22SX2/σ12~F(n−1,m−1)。
成对数据的假设检验 \textcolor{orchid}{\text{成对数据的假设检验}} 成对数据的假设检验
有的时候, X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn和 Y 1 , Y 2 , ⋯ , Y n Y_1,Y_2,\cdots,Y_n Y1,Y2,⋯,Yn之间不一定相互独立, X i X_i Xi与 Y i Y_i Yi之可能有很强的关联,但不同的 ( X i , Y i ) (X_i,Y_i) (Xi,Yi)之间没有关联。在这种情况下我们如何考察均值差呢?
设有 n n n对相互独立的样本 ( X 1 , Y 1 ) , ( X 2 , Y 2 ) , ⋯ , ( X n , Y n ) (X_1,Y_1),(X_2,Y_2),\cdots,(X_n,Y_n) (X1,Y1),(X2,Y2),⋯,(Xn,Yn),令 Z i = Y i − X i ( i = 1 , 2 , ⋯ , n ) Z_i=Y_i-X_i\,(i=1,2,\cdots,n) Zi=Yi−Xi(i=1,2,⋯,n),显然 Z 1 , Z 2 , ⋯ , Z n Z_1,Z_2,\cdots,Z_n Z1,Z2,⋯,Zn相互独立。设 Z 1 , Z 2 , ⋯ , Z n Z_1,Z_2,\cdots,Z_n Z1,Z2,⋯,Zn是来自总体 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)的样本,则可以对 μ \mu μ进行假设检验。一般情况下 σ 2 \sigma^2 σ2是未知的,所以我们选取的检验统计量一般是 T = n ( X ‾ − μ 0 ) S T=\cfrac{\sqrt{n}\left(\overline{X}-\mu_0\right)}{S} T=Sn(X−μ0)。
三、分布假设检验
1. 分布拟合检验的概念
分布拟合检验:设 ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn)是来自总体 X X X的样本,要根据此样本检验假设 H 0 : X 的分布函数为 F ( x ) H 1 : X 的分布函数不是 F ( x ) \begin{aligned} &\textcolor{green}{H_0:X\text{的分布函数为}F(x)}&\\ &\textcolor{red}{H_1:X\text{的分布函数不是}F(x)}& \end{aligned} H0:X的分布函数为F(x)H1:X的分布函数不是F(x)这里 F ( x ) F(x) F(x)是理论分布函数,它可以是已知的,或是形式已知、但包含未知参数的函数。分布拟合检验就是要考察用 F ( x ) F(x) F(x)拟合 X X X的分布时,拟合的优良程度如何?
2. 皮尔逊定理
皮尔逊定理 设一个随机试验的 r r r个结果 A 1 , A 2 , ⋯ , A r A_1,A_2,\cdots,A_r A1,A2,⋯,Ar构成互斥完备事件群,在一次试验中它们发生的概率分别为 p 1 , p 2 , ⋯ , p r p_1,p_2,\cdots,p_r p1,p2,⋯,pr,其中 p i > 0 ( i = 1 , 2 , ⋯ , r ) p_i>0\,(i=1,2,\cdots,r) pi>0(i=1,2,⋯,r),且 ∑ i = 1 r p i = 1 \sum\limits_{i=1}^r p_i=1 i=1∑rpi=1。以 m i m_i mi表示在 n n n次独立重复试验中 A i A_i Ai发生的次数,则当 n → ∞ n\to\infty n→∞时随机变量 χ 2 = ∑ i = 1 r ( m i − n p i ) 2 n p i \chi^2=\sum\limits_{i=1}^r \cfrac{ {(m_i-np_i)}^2}{np_i} χ2=i=1∑rnpi(mi−npi)2的分布收敛于自由度为 r − 1 r-1 r−1的 χ 2 \chi^2 χ2分布。
3. χ 2 \chi^2 χ2拟合检验法
(1) 理论分布 F ( x ) F(x) F(x)完全已知的情形
设 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn是来自总体 X X X的样本, F ( x ) F(x) F(x)是一个完全已知的分布函数,在显著性水平 α \alpha α下,检验假设 H 0 : X 的分布函数为 F ( x ) H 1 : X 的分布函数不是 F ( x ) \begin{aligned} &\textcolor{green}{H_0:X\text{的分布函数为}F(x)}&\\ &\textcolor{red}{H_1:X\text{的分布函数不是}F(x)}& \end{aligned} H0:X的分布函数为F(x)H1:X的分布函数不是F(x)方法如下:
- 将总体 X X X的取值范围划分为 r r r个互不相交的子集(区间) A 1 , A 2 , ⋯ , A r A_1,A_2,\cdots,A_r A1,A2,⋯,Ar,则其构成互斥完备事件群( r r r不大, n n n很大)。注意,样本容量较大,一般 n ≥ 50 n\ge 50 n≥50;分组时每个区间所含样本数 m i ≥ 5 m_i\ge 5 mi≥5。
- 在 H 0 H_0 H0成立的前提下,计算事件 A i A_i Ai的频率为 P ( A i ) = p i P(A_i)=p_i P(Ai)=pi,则事件 A i A_i Ai发生的频数为 n p i np_i npi。
- 统计出样本值 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn中,事件 A i A_i Ai发生的实际频率 m i m_i mi。
- 在显著性水平 α \alpha α下,考虑统计量 χ 2 = ∑ i = 1 r ( m i − n p i ) 2 n p i \chi^2=\sum\limits_{i=1}^r \cfrac{ {(m_i-np_i)}^2}{np_i} χ2=i=1∑rnpi(mi−npi)2。如果数据确实服从 F ( x ) F(x) F(x)规定的分布,那么 χ 2 \chi^2 χ2应该越小越好,所以它的拒绝域应该是 χ 2 \chi^2 χ2大于等于某个数的形式。因此,拒绝域为 χ 2 ≥ χ α 2 ( r − 1 ) \chi^2\ge\chi^2_{\alpha}(r-1) χ2≥χα2(r−1)。
(2) 理论分布含有未知参数的情形
设理论分布为 F ( x ; θ 1 , θ 2 , ⋯ , θ l ) F(x;\theta_1,\theta_2,\cdots,\theta_l) F(x;θ1,θ2,⋯,θl),其中 θ 1 , θ 2 , ⋯ , θ l \theta_1,\theta_2,\cdots,\theta_l θ1,θ2,⋯,θl是未知参数。我们要先干两件事情,然后继续进行理论分布已知时的过程:
- 根据样本 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn求出 θ 1 , θ 2 , ⋯ , θ l \theta_1,\theta_2,\cdots,\theta_l θ1,θ2,⋯,θl的最大似然估计值 θ ^ 1 , θ ^ 2 , ⋯ , θ ^ l \hat{\theta}_1,\hat{\theta}_2,\cdots,\hat{\theta}_l θ^1,θ^2,⋯,θ^l,然后把 F ( x ; θ ^ 1 , θ ^ 2 , ⋯ , θ ^ l ) F(x;\hat{\theta}_1,\hat{\theta}_2,\cdots,\hat{\theta}_l) F(x;θ^1,θ^2,⋯,θ^l)当作完全已知的分布函数处理;
- 千万别忘了把 χ 2 \chi^2 χ2的自由度改为 r − l − 1 r-l-1 r−l−1!!!这是对皮尔逊定理的修正。拒绝域为 χ 2 ≥ χ α 2 ( r − l − 1 ) \chi^2\ge\chi^2_\alpha(r-l-1) χ2≥χα2(r−l−1)。可以理解为,我们需要从 n n n个样本中抽出 l l l个来弥补参数的未知,这造成了自由度的损失,所以最后自由度变成了 r − l − 1 r-l-1 r−l−1。