[机器学习] 贝叶斯分类器1

贝叶斯分类的先导知识

条件概率

所谓条件概率，它是指某事件B发生的条件下，求另一事件A的概率，记为 $P(A|B)$ ，它与 $P(A)$ 是不同的两类概率。

举例： 考察有两个小孩的家庭，其样本空间为 $\Omega = {[bb, bg, gb, gg]}$ , 其中b 代表男孩，g代表女孩，bg表示大的是男孩、小的是女孩，其它点可类似说明

在 $\Omega$ 中4个样本点等可能的情况下，我们来讨论一些事件的概率。

事件 A = “家中至少有一个女孩”发生的概率为
$P (A) = \frac{3}{4}$ $P(A) = \frac{3}{4}$
若已知事件 B = “家中至少有一个男孩” 发生，再求事件 A 发生的概率为
$P (A | B) = \frac{2}{3}$ $P(A|B) = \frac{2}{3}$
这是因为事件B的发生，排除了gg发生的可能。这是样本空间 $\Omega$ 也随之改为 $\Omega_B= [bb, bg, gb]$ ，而在 $\Omega_B$ 中事件A中只含2个样本点，故 $P(A|B) = \frac{2}{3}$ 。这就是条件概率，它与无条件概率 $P(A)$ 是不同的两个概念。
若对上述条件概率的分子分母各除以4，则可得
$P (A | B) = \frac{P (A B)}{P (B)} = \frac{2 / 4}{3 / 4}$ $P(A|B)=\frac{P(AB)}{P(B)}=\frac{2/4}{3/4}$
其中交事件AB = “家中既有男孩又有女孩”。这个关系具有一般性，也就是说，条件概率是两个无条件概率之商。

全概率公式

全概率是概率论中一个重要的公式，它提供了计算复杂事件概率的一条有效途径，使一个复杂事件的概率计算问题化简就繁。

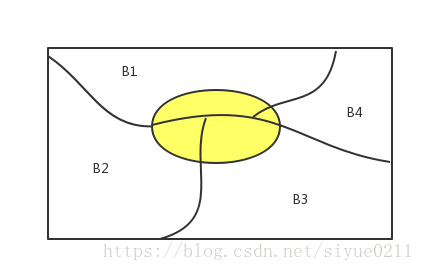
性质：设 $B_1, B_2, ...,B_n$ 为样本空间 $\Omega$ 的一个分割，即 $B_1, B_2,..,B_n$ 互补相容，且 $\bigcup_{i=1}^nB_i = \Omega$ ，如果 $P(B_i)>0$ , i = 1, 2, ..n, 对任一事件A有

P (A) = \sum_{i = 1}^{n} P (B_{i}) P (A | B_{i})

$P(A)=\sum_{i=1}^nP(B_i)P(A|B_i)$
这里写图片描述

证明：因为

A = A Ω = A (⋃_{i = 1}^{n} B_{i}) = ⋃_{i = 1}^{n} (A B_{i})

$A = A\Omega = A(\bigcup_{i=1}^nB_i) = \bigcup_{i=1}^n(AB_i)$
且

A B_{1}, A B_{2} . . ., A B_{n}

$AB_1, AB_2...,AB_n$ 互不相容，所以由可加得

P (A) = P ((⋃_{i = 1}^{n} (A B_{i})) = \sum_{i = 1}^{n} P (A B_{i})

$P(A)=P((\bigcup_{i=1}^n(AB_i))= \sum_{i=1}^nP(AB_i)$ ,再将

P (A B_{i}) = P (B_{i}) P (A | B_{i}), i = 1, 2, . . . n

$P(AB_i)=P(B_i)P(A|B_i), i =1, 2, ...n$ 带入上式即可

贝叶斯公式

在乘法公式和全概率公式的基础上立即可推一个很著名的公式。

性质：设 $B_1, B_2,...B_n$ 是样本空间 $\Omega$ 的一个分割，即 $B_1, B_2,...B_n$ 互补相容，且 $\bigcup_{i=1}^{n}=\Omega$ ,如果 $P(A)>0, P(B_i)>0$ , i = 1, 2, 3, .., n，则

P (B_{i} | A) = \frac{P (B_{i}) P (A | B_{i})}{\sum_{j = 1}^{n} P (B_{j}) P (A | B_{j})}

$P(B_i|A)=\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^{n}{P(B_j)P(A|B_j)}}$
证明：由条件概率的定义

P (B_{i} | A) = \frac{P (A B_{i})}{P (A)}

$P(B_i|A)=\frac{P(AB_i)}{P(A)}$
对上面的式子的分子用乘法公式，分母用全概率公式。

P (A B_{i}) = P (B_{i}) P (A | B_{i})

$P(AB_i) = P(B_i)P(A|B_i)$

P (A) = \sum_{j = 1}^{n} P (B_{j}) P (A | B_{j})

$P(A) = \sum_{j=1}^n{P(B_j)P(A|B_j)}$

举例：某地区的肝癌发病率为0.0004，现在用甲胎蛋白法进行普查，医学研究表明，化验结果是存在错误的，已知患有肝癌的人其检验结果99%呈阳性（有病），而没患肝癌的人其化验结果99%呈阴性（无病）。现某人的检查结果为呈阳性，问他真的患肝癌的概率有多少？

解：记B为事件被检查者患有肝癌， A为事件检查结果呈阳性。
$P(B) = 0.0004$
$P(B')= 0.9996$
$P(A|B) = 0.99$
$P(A|B') = 0.001$

扫描二维码关注公众号，回复： 1506913 查看本文章

我们现在要求：

P (B | A) = \frac{P (B) P (A | B)}{\sum_{j = 1}^{2} P (B_{j}) P (A B_{j})}

$P(B|A)= \frac{P(B)P(A|B)}{\sum_{j=1}^{2}{P(B_j)P(AB_j)}}$

P (B | A) = \frac{P (B) P (A | B)}{P (B) P (A | B) + P (B^{'}) P (A | B^{'})}

$P(B|A)= \frac{P(B)P(A|B)}{P(B)P(A|B) + P(B')P(A|B')}$

P (B | A) = \frac{0.0004 \times 0.99}{0.0004 \times 0.99 + 0.996 \times 0.001} = 0.284

$P(B|A)=\frac{0.0004 × 0.99}{0.0004×0.99+0.996 ×0.001}=0.284$

在上面的例子中，如果我们将事件B“被检测患有肝癌”作为原因，将事件A“检查结果呈阳性”作为最后的结果。则我们在用贝叶斯公式在已知“结果”的条件下，求出了原因的概率P(B|A).

在贝叶斯公式中，如果称 $P(B_i)$ 为 $B_i$ 的先验概率，称 $P(B_i|A)$ 为 $B_i$ 的后验概率，则贝叶斯公式是专门用来计算后验概率的，也就是通过A的发生这个新信息对 $B_i$ 的概率作出修正。

最大似然估计

最大似然估计是求估计常用的一种方法。为了叙述最大似然估计的直观想法，先看两个例子。

例子：设有外形完全相同的两个箱子，甲箱中有99个白球和一个黑球，乙箱有99黑球和一个白球。今随机抽取一箱，并从中随机抽取一球，结果取得白球，问这球是从哪个箱子中取出的？

解：不管是哪个箱子，从箱子中任取一个球都有两个可能的结果：A表示取出白球，B表示取出黑球。如果我们取出的是甲箱子，则A发生的概率0.99，如果我们取出的是乙箱，则A发生的概率0.01。现在一次实验中结果A发生了，人们的第一印象是：这个求最像从甲箱中取出的。或者说，应该认为试验条件对结果A出现有利。从而可以推断这球是从甲箱子中取出的。这个推断很符合人们的经验事实，这里“最像”就是最大似然的意思。

例子：
设一个试验有三种可能的结果，其概率分别为： $p_1 = \theta^2$ ， $p_2 = 2\theta(1-\theta)$ , $p_3 = (1-\theta)^2$ 。现做了n次试验，观察到三种结果发生的次数分别是 $n_1, n_2, n_3(n_1+n_2+n_3=n)$ ，则似然函数是

L (θ) = (θ^{2})^{n_{1}} [2 θ (1 - θ)]^{n_{2}} [(1 - θ)^{2}]^{n_{3}}

$L(\theta) = (\theta^2)^{n_1}[ 2\theta(1-\theta)]^{n_2}[ (1-\theta)^2]^{n_3}$

L (θ) = 2^{n_{2}} θ^{2 n_{1} + n_{2}} (1 - θ)^{2 n_{3} + n_{2}}

$L(\theta)=2^{n_2}\theta^{2n_1+n_2}(1-\theta)^{2n_3+n_2}$
我们现在希望

L (θ)

$L(\theta)$ 尽可能的大，它现在表示的就是从当前的结果看，最拟合真实概率分布的函数式。

L (θ)

$L(\theta)$ 称为样本的最大似然函数。则我们当前的目标是求得一个

θ

$\theta$ 使得

L (θ)

$L(\theta)$ 最大。
则对数似然函数为

l n L (θ)) = (2 n_{1} + n_{2}) l n^{θ} + (2 n_{3} + n_{2}) l n^{1 - θ} + n_{2} l n^{2}

$ln L(\theta))=(2n_1+n_2)ln^{\theta}+(2n_3+n_2)ln^{1-\theta}+n_2ln^2$
将之关于

θ

$\theta$ 求导，并令其为0得到似然方程。

\frac{2 n_{1} + n_{2}}{θ} - \frac{2 n_{3} + n_{2}}{1 - θ} = 0

$\frac{2n_1+n_2}{\theta}-\frac{2n_3+n_2}{1-\theta}=0$
结果

θ = \frac{2 n_{1} + n 2}{2 n}

$\theta=\frac{2n_1+n2}{2n}$
再对

L (θ)

$L(\theta)$ 求二阶导数，小于0，所以是极大值点。

下一集：贝叶斯分类器2

参考

概率论与数理统计教程
机器学习实战
机器学习（西瓜书）