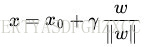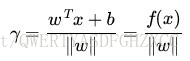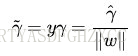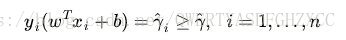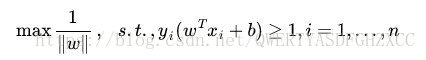1.1、线性分类的例子
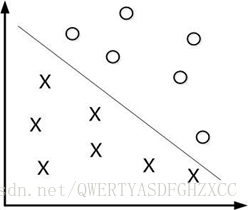
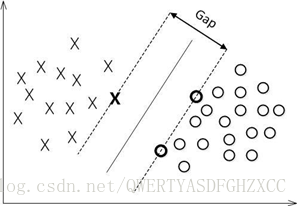
如下图所示,现在有一个二维平面,平面上有两种不同的数据,分别用圈和叉表示。由于这些数据是线性可分的,所以可以用一条直线将这两类数据分开,这条直线就相当于一个超平面,超平面一边的数据点所对应的y全是-1 ,另一边所对应的y全是1。
这个超平面可以用分类函数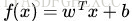
接下来的问题是,如何确定这个超平面呢?从直观上而言,这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线对于直线两边的数据的最小间隔最大化。这里的最小间隔指的是对于固定的超平面而言,数据距离超平面的最小间隔;最大化指的是通过比较不同超平面的最小间隔,选取最小间隔最大的那个超平面,也就是最适合的超平面。
1.2、函数间隔与几何间隔
在超平面w*x+b=0确定的情况下,|w*x+b|能够表示点x到距离超平面的远近,而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确,所以,可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此,我们便引出了函数间隔的概念。
定义函数间隔(用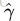
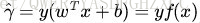
而超平面(w,b)关于T中所有样本点(xi,yi)的函数间隔最小值(其中,x是特征,y是结果标签,i表示第i个样本),便为超平面(w, b)关于训练数据集T的函数间隔:
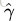
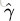
但这样定义的函数间隔有问题,即如果成比例的改变w和b(如将它们改成2w和2b),则函数间隔的值f(x)却变成了原来的2倍(虽然此时超平面没有改变),即对于任意超平面,都可以通过成比例的增大w和b来使其对应的 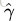
事实上,我们可以对法向量w加些约束条件,从而引出真正定义点到超平面的距离--几何间隔的概念。
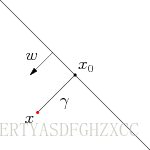
假定对于一个点 x ,令其垂直投影到超平面上的对应点为 x0 ,w 是垂直于超平面的一个向量,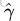
根据平面几何知识,有
其中||w||为w的二阶范数(范数是一个类似于模的表示长度的概念),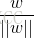
又由于 x0是超平面上的点,代入超平面的方程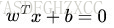
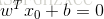
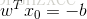
随即让此式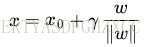
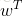


为了得到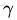
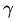
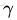
从上述函数间隔和几何间隔的定义可以看出:几何间隔就是函数间隔除以||w||,而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|,只是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。
1.3、最大间隔分类器
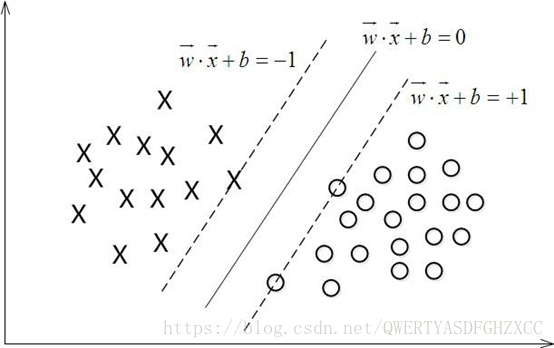
对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。
通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得 
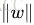
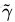
于是最大间隔分类器的目标函数可以定义为:
同时需满足一些条件,根据间隔的定义,有
其中,s.t.,即subject to的意思,它导出的是约束条件。
回顾下几何间隔的定义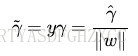
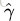


相当于在相应的约束条件 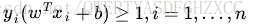
这里证明下为什么可以令 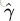
如下图所示,中间的实线便是寻找到的最优超平面,其到两条虚线边界的距离相等,这个距离便是几何间隔 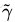
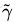
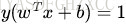

1.4、引出问题
①线性不可分怎么办?
②如何最优化目标函数?