Logistic回归——二分类 —— matlab

1.简介

2.应用范围

3.分类

1.简介

Logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，Logistic回归虽说是回归，但实际更属于判别分析。

2.应用范围

① 适用于流行病学资料的危险因素分析

② 实验室中药物的剂量-反应关系

③ 临床试验评价

④ 疾病的预后因素分析

3.分类

①按因变量的资料类型分：

二分类

多分类

其中二分较为常用

② 按研究方法分：

条件Logistic回归

非条件Logistic回归

两者针对的资料类型不一样，前者针对配对研究，后者针对成组研究。

3.应用条件

① 独立性。各观测对象间是相互独立的；

② LogitP与自变量是线性关系；

③ 样本量。经验值是病例对照各50例以上或为自变量的5-10倍（以10倍为宜），不过随着统计技术和软件的发展，样本量较小或不能进行似然估计的情况下可采用精确logistic回归分析，此时要求分析变量不能太多，且变量分类不能太多；

④ 当队列资料进行logistic回归分析时，观察时间应该相同，否则需考虑观察时间的影响（建议用Poisson回归）。

4.原理详解

4.1 sigmod分类函数

之所以在这里介绍，是因为下面会用到这个函数

Sigmoid函数：

$\large h_{w}=\frac{1}{1+e^{-z}}$

曲线表示：

由图可见当范围为0-1,当X<0时，Y趋向于0，X>0时，Y趋向于1，适合用于0-1二分类。

所以我们就可以设分类函数如下：

$\large h_{w}=\frac{1}{1+e^{-z}}$

$\large z=\omega ^{T}x$

$\large x=\begin{bmatrix} 1,x_{1},x_{2},...,x_{n}\end{bmatrix}$

$\large z=w_{0}+w_{1}x_{1}+...+w_{n}x_{n}$

其中 $x$ 为自变量，即特征数据。实际因变量为 $y$ ，为0-1变量, $h_w$ 为预测值范围为0-1。显然这个模型需要求解的变量为 $w$ 。

4.2 建立目标函数

对于输入变量 $x$ ，设 $h_w(x)$ 为输出为1的概率，则 $1-h_w(x)$ 为输出0的概率。则可表示成如下：

$\large p(y=1|x;w)=h_{w}(x)$

$\large p(y=0|x;w)=1-h_{w}(x)$

求解损失函数：用概率论中的极大似然估计的方法，构建概率函数如下，

$\large P(y|x;w)=(h_{w}(x))^{y}*(1-h_{w}(x))^{1-y}$

对损失函数可以理解为，当 $y=1$ 时， $h_w(x)$ 的值越大，P的值越大； $y=0$ 时， $h_w(x)$ 的值越小，P的值越小。即可以认为，当P值越大时预测的越准确。单个输入的目标即为P取最大。对M个输入样本，可以构建以下目标函数：

$\large L(w)=\prod_{i=1}^{m}(h_{w}(x))^{y^{(i)}}*(1-h_{w}(x))^{1-y^{(i)}}$

对目标函数取对数可以将目标函数的连乘变为连加：

$\large log(L(w))=\sum_{i=1}^{m}y^{(i)}h_{w}(x^{(i)})+(1-y^{(i)})(1-h_{w}(x^{(i)}))$

4.3 求解相关参数

设 $J(w)=log(L(w))$ ，求 $J(w)$ 的最大值，可以用梯度上升的方法进行求解，如果在前面加上一个负号，则就转化为梯度下降。在这里用梯度上升法求解系数 $\large w$ ：

$\large w^{'}=w+\eta \triangledown J(w)$

其中， $\large \eta$ 为学习率。 $\triangledown J(w)$ 对目标函数求梯度、即求导。

$\large \eta \triangledown J(w)^{(i)}=\frac{\partial J(w)^{(i)} }{\partial w}$

$\large =[\frac{y^{(i)}}{h_{w}(x^{(i)})}+\frac{1-y^{(i)}}{1-{h_{w}(x^{(i)})}}]\frac{\partial h_{w}(x^{(i)}) }{\partial w}$

$\large =[\frac{y^{(i)}-h_{w}(x^{(i)}}{h_{w}(x^{(i)})(1-{h_{w}(x^{(i)})})}]\frac{\partial h_{w}(x^{(i)}) }{\partial w}$

其中：

$\large \frac{\partial h_{w}(x^{(i)}) }{\partial w}=(\frac{1}{1+e^{-w^{T}x^{(i)}}})^{'}=\frac{x^{(i)}e^{-w^{T}x^{(i)}}}{(1+e^{-w^{T}x^{(i)}})^{2}}$

$\large =x[\frac{1}{1+e^{-w^{T}x^{(i)}}}\times \frac{e^{-w^{T}x^{(i)}}}{1+e^{-w^{T}x^{(i)}}}]$

$\large =x[h_{w}(x^{(i)})(1-h_{w}(x^{(i)}))]$

将其带入原式可得：

$\large \triangledown J(w)^{(i)}=x^{(i)}[y^{(i)}-h_{w}(x^{(i)})]$

$\large \triangledown J(w)=\sum_{i=1}^{m}x^{(i)}[y^{(i)}-h_{w}(x^{(i)})]$

5.实列分析

5.1 读取数据（excel文件）

data=xlsread('D:\桌面\data.xlsx')

返回：发现数据直接从不是标题的第一行开始读取了

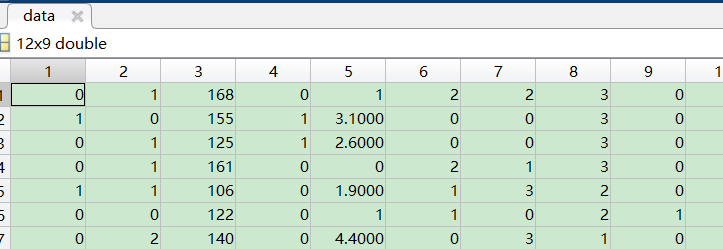
5.2 分离数据集

正式介绍之前补充一点东西

行数 = size(data,1)

列数 = size(data,2)

好，开始进入正题

此为通过比例确定，选择多少行数据作为测试集

num=round(0.8*size(data,1));%取整个数据0.8的比例训练

此为，选出相应比例的数据作为测试集

train_data=data(1:num,:)

此为，将剩余数据作为验证集

test_data=data(num+1:end,:)

分离测试集的x和y

n=size(data,2)
train_y=train_data(:,n); %确定y所对应的数据
train_x=train_data(:,1:n-1); %除去y将剩余的数据都归于x

同理分离验证集的x和y

test_y=test_data(:,n); 
test_x=test_data(:,1:n-1);

5.3 求解前设定

详看上面过程公式4.1的分类函数的解析

train_x1=[ones(size(train_x,1),1),train_x];%在基础上增加常数项
test_x1=[ones(size(test_x,1),1),test_x];
w=zeros(size(train_x1,2),1);
lr=0.001;%学习率

5.4 求解目标函数

pred_f=  train_x1*w;  %预测出的方程式取值
pred_y=1./(1+exp(-pred_f)); %Sigmoid函数
d_w=(train_y-pred_y)'*train_x1;
w=w+lr*d_w';

pred_y=1./(1+exp(-test_x1*w)) %%Sigmoid函数预测出的y

fenlei=(pred_y>=0.5)

accu=1-sum(abs(fenlei-test_y))./length(test_y)

我们用预测的和原始数据对比一下，确实是只对了一个

6.matlab自带函数

fitglm

官方文档：Create generalized linear regression model - MATLAB fitglm- MathWorks 中国

Create generalized linear regression model 创建广义线性回归模型

mdl = fitglm(x,y,'distribution','binomal') 构建二项式 logistic模型

接下来我们再对上述数据进行拟合

数据集划分部分就不重复了

GM= fitglm(x,y);
y_p = predict(GM,x_t);
fenlei=(y_p>=0.5)
accu=1-sum(abs(fenlei-y_t))./length(y_p)

可以发现和上面结果一致。

线性回归结果分析：

1. 回归系数置信区间应不包含零点

2. stats统计量：

1） $R^{2}$ ： $R^{2}$ 的值越接近 1，变量的线性相关性越强，

2）F ：当 F > F1-α(m,n-m-1) ，即认为因变量 y 与自变量 x1,x2,...,xm 之间有显著的线性相关关系；

否则认为因变量 y 与自变量 x1,x2,...,xm 之间线性相关关系不显著。

3）p ：若 p < α（α 为预定显著水平），则说明因变量 y 与自变量 x1,x2,...,xm之间显著地有线性相关关系。

4） $s^{2}$ 主要用来比较模型是否有改进，其值越小说明模型精度越高。

本次就到这里了，如果有错误的话及时联系我进行改正哦，谢谢。

fbs	restecg	thalach	exang	0ldpeak	sl0pe	ca	thal	target
0	1	168	0	1	2	2	3	0
1	0	155	1	3.1	0	0	3	0
0	1	125	1	2.6	0	0	3	0
0	1	161	0	0	2	1	3	0
1	1	106	0	1.9	1	3	2	0
0	0	122	0	1	1	0	2	1
0	2	140	0	4.4	0	3	1	0
0	0	145	1	0.8	1	1	3	0
0	0	144	0	0.8	2	0	3	0
0	0	116	1	3.2	1	2	2	0
0	1	125	0	1.6	1	0	2	1
1	0	136	1	3	1	0	3	0