在这一章里，我们将探索四旋翼无人机动力学的相关知识。我将主要讲刚体动力学中的牛顿-欧拉方程以及在四旋翼无人机上的形式。

上一章链接：

Robotics: Aerial Robotics（空中机器人）笔记（三）:无人机运动学

四旋翼无人机合力与合力矩分析

与之前的讨论相同，我们将讨论两个坐标系。一个是移动机器人上的坐标系，另一个是惯性坐标系。四旋翼无人机上有四个转子，每个转子都是电机独立驱动的。 r 是质心的位置向量，并且我们知道每个电机产生的升力和相应的阻力矩，那么四旋翼无人机的合力以及合力矩也可以求出：

为了求出四旋翼无人机的加速度，我们必须引入牛顿-欧拉方程。

牛顿-欧拉方程（Newton-Euler Equations）

我们把刚体当作一个由无数个粒子组成的系统，每个粒子的运动符合牛顿第二定律：

那么我们考虑牛顿第二定律下的由粒子组成的系统：

首先我们要定义系统的质心 C，可以通过以下的公式求得，其中 $p_i$ 是系统中每个粒子的位置矢量， $m_i$ 是每个粒子对应的质量， $m$ 是刚体的质量：

事实证明，粒子系统的质心 C 在惯性系 A 中加速，就好像它是一个质量为 $m$ （等于系统总质量）的单个粒子，受到的力等于合外力。所以我们就有如下式子，其中加速度 $\textbf{a}$ 是速度 $\textbf{v}$ 的微分，上标 A 表示正在计算所有这些量都在一个惯性系 A 中，而上标 C 指的是正在计算质心的速度：

那么通过高中物理的学习我们可以知道动量 $\textbf{p}=m\textbf{v}$ ，那么我们就可以得到合力等于其线动量的变化率：

其中 $\textbf{L}$ 指的是粒子系统的线动量。

考虑完平动，那么我们就来考虑旋动了。由力和力矩的对应关系我们就可以得到其合力矩应为其角动量的变化率，其中 H 是惯性系 A 以刚体 B 的质心 C 为原点的的角动量：

角动量的表达如下，其中 $\mathbf{I}_C$ 是以 C 为原点的惯性张量， $^A\omega^B$ 是刚体 B 在惯性系 A 上的角速度：

主惯性轴和主惯性矩（Principal Axes and Principal Moments of Inertia）

这门课上关于主惯性轴和主惯性矩的内容讲的稍微有些跳跃，所以我以我的理解以及网上对此的相关介绍来说明。

转动惯量

我们首先讲一下转动惯量，它是一个用来衡量做旋转运动的物体由静止状态变为旋转状态或者由旋转状态变为静止的物理量。在物体做平动运动中，与转动惯量对应的就是物体的惯性，其与质量有关。而转动惯量不单与质量有关，还与旋转物体的质量相对于回转轴的分布状态有关。

对于一般物体，其绕某一轴z的转动惯量计算公式如下：

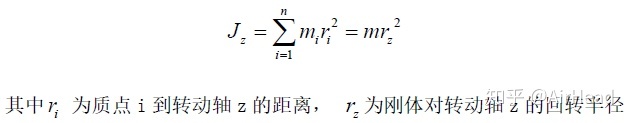
惯性张量

作为转动惯量的推广，惯性张量是刚体绕某一点转动时惯性的量度，惯性张量与点的选取、坐标系的选取和刚体本身质量分布有关：

$I=\begin{bmatrix} I_{xx}&-I_{xy} &-I_{xz} \\ -I_{xy}&I_{yy} &-I_{yz} \\ -I_{xz}&-I_{yz} &I_{zz} \end{bmatrix}$

其中， $I_{xx}$ ， $I_{yy}$ 和 $I_{zz}$ 为惯性矩，其它元素称之为惯性积。这里只是稍微过一个知识点，每个元素具体的计算公式感兴趣的同学们可以自行去查。

主惯性轴和主惯性矩

如果选取的坐标系oxyz与刚体在o点的三个惯性主轴相重合，则惯性积均为0，这时惯性张量为对角矩阵，称此时的坐标系各轴为惯性主轴，相应的惯性矩为主惯性矩。

那么此时的惯性张量如下：

$I=\begin{bmatrix} I_{xx}&0 &0 \\ 0&I_{yy} &0 \\0&0 &I_{zz} \end{bmatrix}$

下图中左边部分就是选取的坐标系oxyz没有与刚体在o点的三个惯性主轴重合的情况，我们可以看出角动量矢量与角速度矢量此时不是平行的。而右边则是重合的情况，此时角动量矢量与角速度矢量平行。惯性张量就只剩下惯性矩，可以让计算更加方便。

欧拉运动方程（Euler's Equations of Motion）

有了前面的铺垫，我们就可以来计算相应的刚体运动方程了。我们在刚体上选取一个坐标系 B ，这个坐标系就是沿着刚体的三个惯性主轴，原点为质心 C 建立起来的，它固定在了刚体上，所以称之为刚体系。如下图所示：

角速度也就可以分解成这三个方向上的量：

还记得之前求合力矩的公式吗？

我们可以把它分解成两项相加，其中第一项是在角动量在刚体系上求导，第二项是一个修正因子，对第一项进行相关修正。这个修正因子将刚体坐标系的角速度与角动量进行了叉乘，实际上是一个在力学领域中非常常见的概念，在运动坐标系中对某向量进行求导的结果与在固定坐标系中的是不同的：

其中第一项可以写成：

那么最终的合力矩在三个方向上的分量就可以求出来：

这便是欧拉运动方程，在接下来的内容中我们将使用 p，q 和 r 来表示沿 b1，b2 和 b3 的角速度向量：

四旋翼无人机运动方程（Quadrotor Equations of Motion）

回到之前说的，我们已经知道了四旋翼无人机的合力和合力矩：

那么根据牛顿-欧拉方程我们可以得到如下的表达式，其中 R 是刚体系 B 旋转到惯性系 A 的旋转矩阵，L 是每个转子到质心的长度，事实上我们需要知道的就只是一些几何结构的参数，例如质量，力矩长度等，这些参数的测量比较容易：

通过上式我们也可以得到角速度与欧拉角变化之间的关系：

这个式子的推导如下：

在Z-X-Y欧拉角中，旋转矩阵为：

$R=R_z(\psi)R_x(\phi)R_y(\theta)$

由第三章四旋翼无人机的运动学的学习中我们知道，其以角速度为特征的反对称矩阵如下，并将上式代入到下式得到：

$\hat{w_b}=(p \ q\ r)\hat{} = R^T\dot{R}$

$=R_y^T\dot{R}_y+R_y^T(R_x^T\dot{R}_x)+R_y^TR_x^T(R_z^T\dot{R}_z)R_xR_y$

我们知道 $R^T\dot{R}$ 对应的是总的角速度，那么 $R_y^T\dot{R}_y$ 对应的就是 y 上的角速度，其它同理：

$R_x(\phi)^T\dot{R}_x(\phi) = (\dot{\phi} \ 0 \ 0)\hat{}$

$R_y(\theta)^T\dot{R}_y(\theta) = (0\ \dot{\theta} \ 0)\hat{}$

$R_z(\psi)^T\dot{R}_z(\psi) = (0 \ 0 \ \dot{\psi} )\hat{}$

运用矩阵积和叉积的相关性质 $Rw \times Rv = R(w\times v)$ ，我们可以得到：

$(Rw)\hat{}Rv = R\hat{w}v$

那么就有，其中 R 是正交矩阵，所以 $RR^T$ 为单位矩阵：

$(Rw)\hat{}R = R\hat{w} \ \ \ \ \ \ \ or \ \ \ \ \ \ (Rw)\hat{} = R\hat{w}R^T$

我们再看回原式，是不是就可以写成如下形式，然后把帽子摘下：

$(p \ q\ r)\hat{} = (0 \ \dot{\theta} \0)\hat{} + [R_y^T(\dot{\phi} \0 \0)]\hat{} + [R_y^TR_x^T(0 \0 \ \dot{\psi})]\hat{} \\$

$(p \ q\ r) = (0 \ \dot{\theta} \0) + [R_y^T(\dot{\phi} \0 \0)] + [R_y^TR_x^T(0 \0 \ \dot{\psi})]$

接下来把 $R_y, R_x$ 代进去：

$R_y=\begin{bmatrix} cos\theta&0 &sin\theta \\ 0&1 &0 \\ -sin\theta&0 &cos\theta \end{bmatrix} \ \ \ \ R_x = \begin{bmatrix} 1&0 &0 \\ 0&cos\phi &-sin\phi \\ 0&sin\phi &cos\phi \end{bmatrix}$

得到：

$\begin{bmatrix} p\\ q\\ r \end{bmatrix}= \begin{bmatrix} \dot{\phi}cos\theta-\dot{\psi}cos\phi sin\theta\\ \dot{\theta}+\dot{\psi}sin\phi\\ \dot{\phi}sin\theta+\dot{\psi}cos\phi cos\theta \end{bmatrix}= \begin{bmatrix} cos\theta &0 &-cos\phi sin\theta \\ 0 &1 &sin\phi \\ sin\theta&0 &cos\phi cos\theta \end{bmatrix}\begin{bmatrix} \dot{\phi}\\ \dot{\theta} \\ \dot{\psi} \end{bmatrix}$