目录
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结,并讨论在在PCA降维算法中是如何运用运用SVD的。
一、特征值分解(EVD)
如果矩阵A是一个m × m的实对称矩阵(即A= ),那么它可以被分解成如下的形式
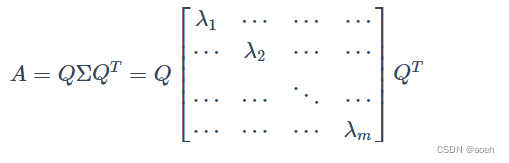
其中Q为标准正交阵,即有,Σ 为对角矩阵,且上面的矩阵的维度均为m×m。
称为
特征值, 是Q(特征矩阵)中的列向量,称为
特征向量。
上面的特征值分解,对矩阵有着较高的要求,需要A为实对称矩阵。
但是一般的矩阵分解呢?这就需要我们接下来介绍的,矩阵奇异值分解。
二、奇异值分解(SVD)
有一个m×n的实数矩阵A,我们想要把它分解成如下的形式
其中U和V均为单位正交阵,即有和
,U称为
左奇异矩阵,V称为右奇异矩阵,Σ仅在主对角线上有值,我们称它为奇异值,其它元素均为0。上面矩阵的维度分别为。
一般地Σ有如下形式:
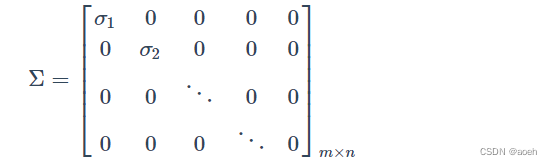
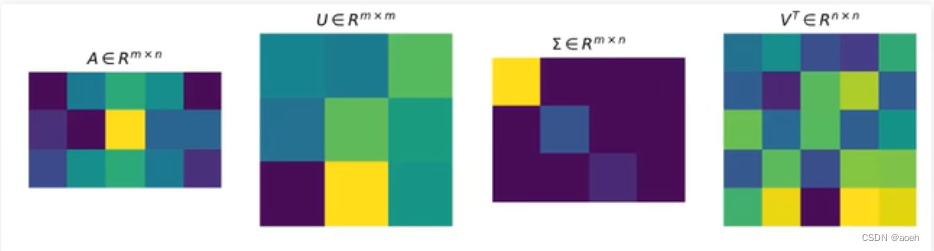
对于奇异值分解,我们可以利用上面的图形象表示,图中方块的颜色表示值的大小,颜色越浅,值越大。对于奇异值矩阵Σ,只有其主对角线有奇异值,其余均为0。
奇异值求解
利用如下性质求 U,V,Σ
需要指出的是,这里 与
在矩阵的角度上来讲,它们是不相等的,因为它们的维数不同
,而
,但是它们在主对角线的奇异值是相等的,即有
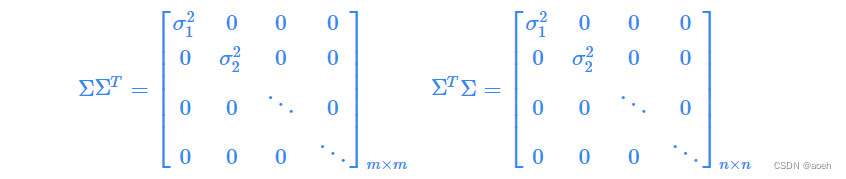
对或
中的特征值开方,可以得到所有的奇异值。
svd-python实现
numpy自带svd函数
import numpy as np
def svd(M):
"""
Args:
M: numpy matrix of shape (m, n)
Returns:
u: numpy array of shape (m, m).
s: numpy array of shape (k).
v: numpy array of shape (n, n).
"""
u,s,v = np.linalg.svd(M)
return u, s, v