最小二乘在直线拟合上的应用
在前一篇最小二乘的文章中:
我们知道了:1,正规方程, 2,计算最优解的方法,3,计算投影的方法

在这篇文章中,我会从最小二乘在拟合直线上的应用开始,先是用实例来说明最小二乘的实际应用。紧接着,我会从这个例子出发,循序渐进的引出为什么我们希望A的列向量不仅仅是相互独立的,更希望他们是相互正交的。从而导出,如何令A的列向量彼此正交,这就是著名的Gram-Schmidt正交化。(需要再次重申的是,学习不是为了考试,不是为了背公式,更不需要题海战术,而是“知其(Gram-Schmidt)然,知其(Gram-Schmidt)所以然”)
拟合直线
拟合直线可以说是最小二乘最好的应用之一。简而言之,就是用m>2个点(也可以说是m个观测点,及其所对应的m个数据)去拟合一条直线。
对某个实验而言,如果他的实验结果是线性的,且没有任何实验误差,则两次实验的结果就能确定一条符合这一实验规律的直线b=C+Dt,而且后续所有的实验结果都应当落在这条直线上。假定现有m个实验结果,他们在横坐标上的值为,
,...,
,他们在纵坐标中所对应的值分别是
,
,...,
。现在我们用方程
=C+D
表示一条穿过这些点的直线,得到如下方程组:
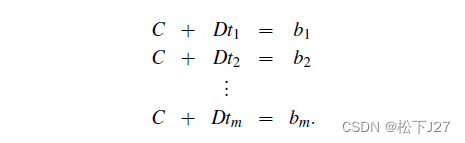
如果m个实验结果都没有误差,则,上述方程组有解,且有唯一解C,D。但,如果实验结果有误差,则不可能找到一个完美的C,D,让这条直线穿过所有的点。这是一个(overdetermined system)超定方程组,m>2个方程,2个未知数,方程组无解。用矩阵来表示为:
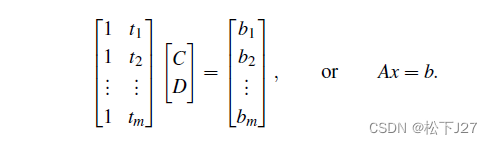
因实验结果的误差导致方程组无解,因此,我们只能找一条尽可能贴近所有点的直线。对于矩阵A而言,他有两个列向量,方程组无解,所以无法通过线性组合得到等式右端的列向量。在维持A的两个列向量不变的情况下,我们通过新的线性组合,
,在A的列空间中找到了最接近向量b的向量p,即,b在A的列空间C(A)上的投影。
同时,也最小化了每个点与直线之间的纵向误差,即,最小化
。其中,
。(但这不是我推崇的思维,应该优先考虑用投影的角度思考!)
方程左右两边同时乘以,得到“正规方程”:
(或
,其中P为投影矩阵)
其中等式左边等于:

等式右边等于:

最终得到:
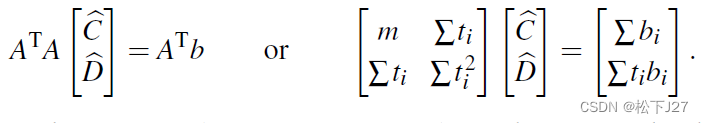
Example 1:

如图,现有三个数据点分别是(注意,他们并不是等间隔的):
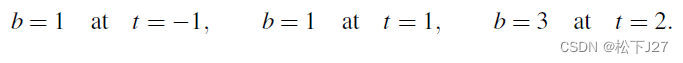
对应的方程组为:

方程组无解,因为这三点不在一条直线上。通过求解最小二乘方程组,即,联立正规方程组,得到最优解:
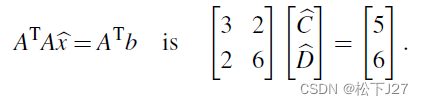
最终得到最优解为,,
,最好的拟合直线为
。
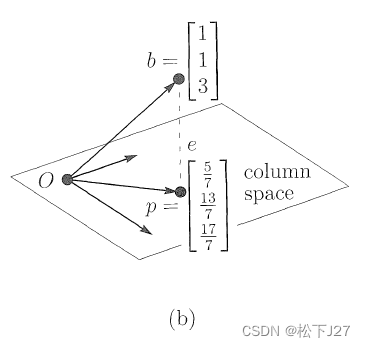
最小二乘法用在线上的点 p 替换不在线上的点 b!