AcWing 算法基础课笔记 3.搜索与图论（持续更新）

---

深度优先遍历DFS与宽度优先遍历BFS

二者对比

都可以对整个搜索空间进行遍历。
搜索的时候都是像一棵树一样搜索。

但是搜索的顺序不一样：
DFS 优先深度，到不能再前进的时候（叶子节点）再回溯。
BFS 一层层搜索，搜索完每一代节点后，再搜索下一代节点。

	DFS	BFS
数据结构	stack	queue
空间	O(h)	O(2h)

DFS 在空间使用上有优势，但不具有最短路性。
BFS 有一个最短路的概念，即假设树中每条边的权重均为1， BFS 搜索到某一个点的路径，一定是最短距离。

最小步数、最短距离，最少操作等：BFS
算法思路较奇怪或者空间要求较高：DFS

DFS

最重要的考虑点在于：顺序。决定要以什么样的顺序来遍历所有方案。

例题：

DFS搜索树构建如下，红线为搜索顺序

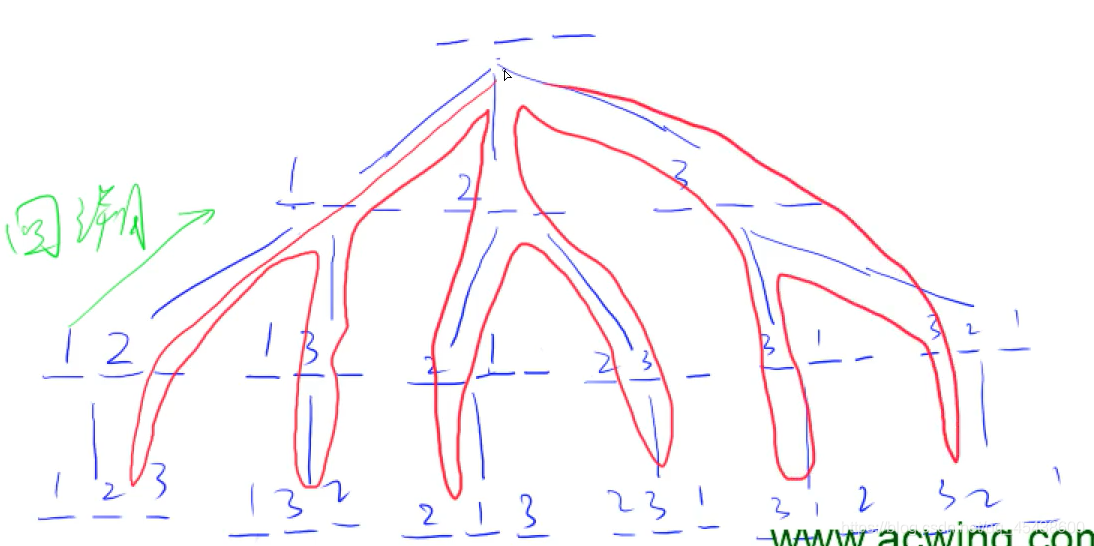
回溯时不要忘了恢复现场，即回溯前是什么样，回溯后还应时什么样。

还有 n-皇后问题，回溯+剪枝。（经典题，不赘述，站内讲解很多。）

BFS

框架：

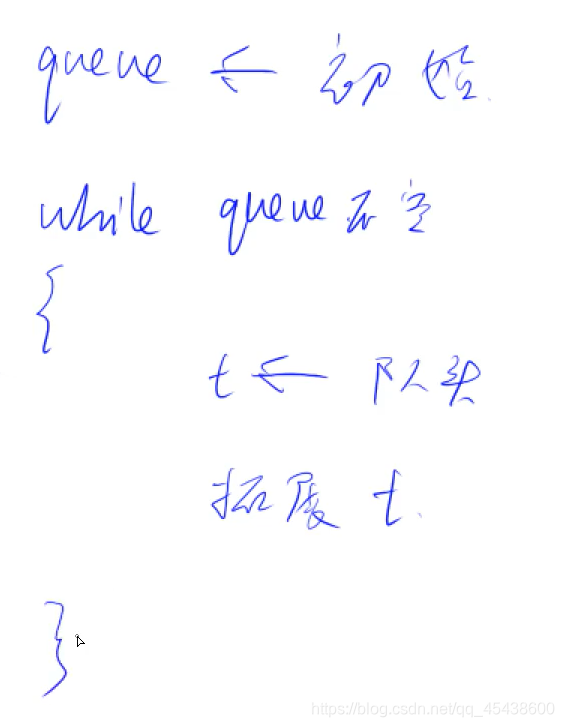
树与图

树与图的存储

基本思想

树是一种特殊的图（无环连通图），所以只讲图就可以了。
图分有向图和无向图，有向图建立一条有向边，无向图建立两条有向边，所以可将无向图看作一种特殊的有向图，故只需将有向图。

存储方式两种：

1. 邻接矩阵（用的较少） g[a, b]，不能保存重复链接，空间复杂度为 n²，较适合存储稠密图。
2. 邻接表（用的多） 在数组的每个节点上都有一个单链表。每次插入一个链接时，在单链表头部插入（头插法）。
   

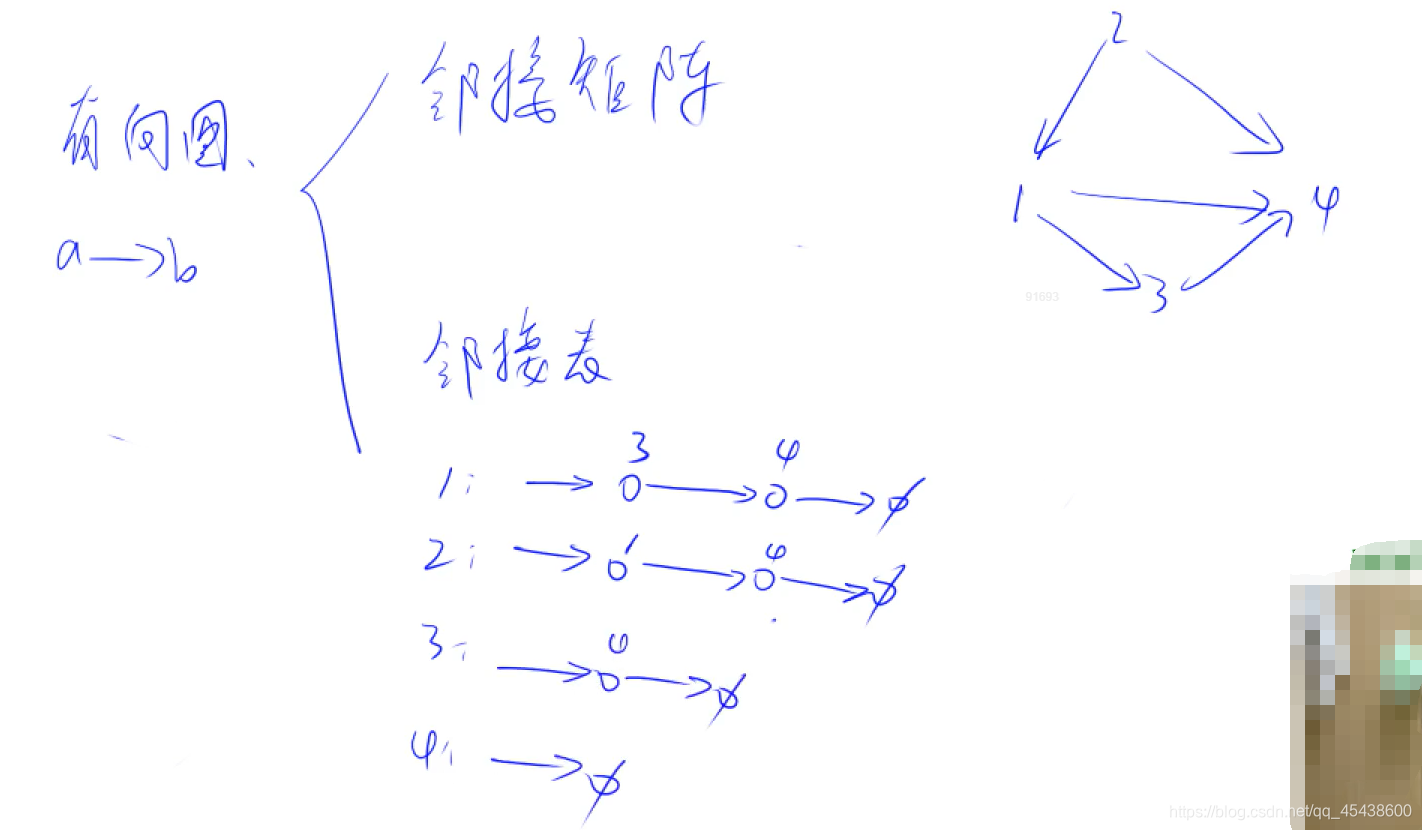
树与图的存储模板

1. 邻接矩阵

g[a][b] 存储边a->b

2. 邻接表

// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;

// 添加一条边a->b
void add(int a, int b)
{
    
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);

树与图的遍历

基本思想

主要指树与图的深搜、宽搜
其实和上面DFS、BFS区别不大，只是套用于图中即可。

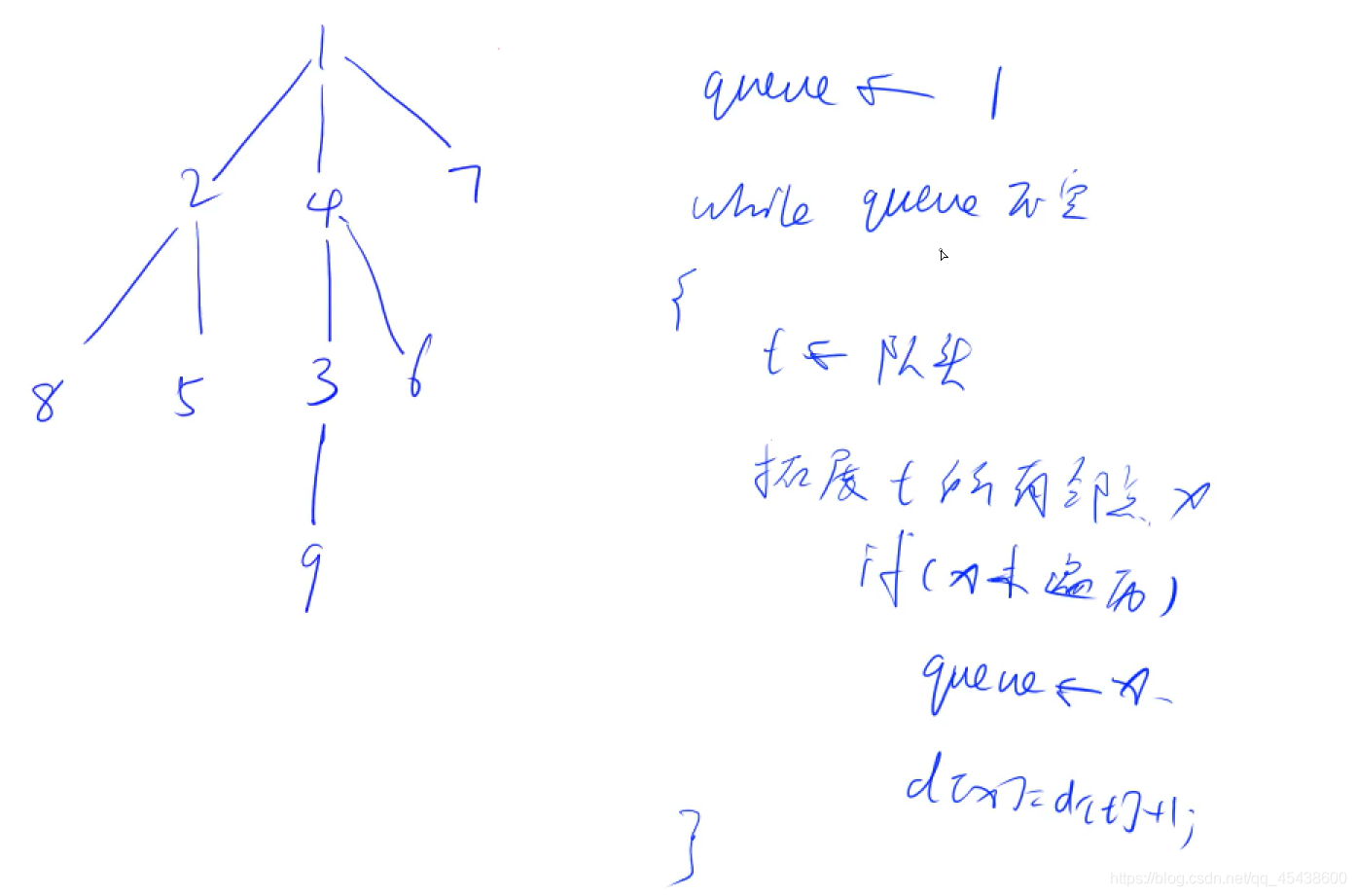
树与图的遍历模板

时间复杂度 O(n+m), n 表示点数，m 表示边数

1. 深度优先遍历

int dfs(int u)
{
    
    
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
    
    
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

2. 宽度优先遍历

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    
    
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
    
    
        int j = e[i];
        if (!st[j])
        {
    
    
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

拓扑排序

针对有向图，无向图没有拓扑序列。

定义：若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x, y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。

eg：对于下图，1 2 3 就是一个拓扑序列。

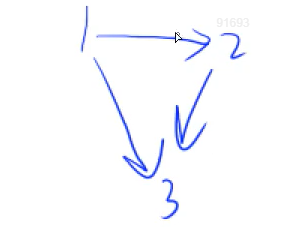
可以证明，一个有向无环图，一定有拓扑序列，所以也叫拓扑图。
一个有向无环图一定存在一个入度为 0 的点。

编程实现思路：

拓扑排序模板

时间复杂度 O(n+m)， n 表示点数，m 表示边数

bool topsort()
{
    
    
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
    
    
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
    
    
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}

附
有些较复杂的懒得写特别细，建议AcWing学一下y总的课效果更好。
以上截图和模板均来源：AcWing
链接：https://www.acwing.com/blog/content/404/