灰色预测

前言
一、灰色预测的基础知识
二、灰色分析
三、灰色系统建模
四、模型的改进
四、实战模拟
参考资源
总结（一些很久没更的唠嗑）

前言

个人认为《数学建模算法与应用（第三版）》这本书还是比较深入浅出的，遇到难一些的建模问题可能不太够用，所以这里大部分内容参考了《预测理论与方法及其MATLAB实现》的内容，保证灰色系统的学习更加系统化、深入化。

灰色预测理论是我国学者邓聚龙于1982年首先提出的一种处理不完全信息的理论方法。
灰色预测通过鉴别系统因素之间发展趋势的相异程度，进行关联分析，并对观测到的反映预测对象特征的一系列数值进行灰色生成处理，然后建立相应的微分方程模型，来预测事物未来发展的趋势。

一、灰色预测的基础知识

1.1 灰数

灰数是灰色系统理论的基本单元，指在某个区间或某个一般的数集内取值的不确定数。灰数是区间数的一种推广，记为 $\oplus$

分类：
（1）仅有下界的灰数
（2）仅有上界的灰数
（3）区间灰数
（4）连续灰数与离散灰数
（5）黑数与白数
（6）本征灰数与非本征灰数

从本质上看，灰数又可以分为信息型、概念型和层次型三类。信息类灰数是指由于信息缺乏而不能肯定其取值的数；概念型灰数指人们由于某种意愿、观念形成的灰数；层次型灰数是指由于层次改变而形成的灰数。

1.2 灰数白化与灰度

对于一般的区间灰度 $\oplus\in [a,b]$ ，将白化值取为 $\widetilde{\oplus}=\alpha a+(1-\alpha)b,\alpha\in [0,1]$
一般而言，灰数的白化取决于信息的多少，如信息量大较大则白化比较容易。
灰数的灰度在一定程度上反映了人们对灰色系统的行为特征的未知程度。

1.3 灰色序列生成算子

灰色理论认为：任何随机过程都是在一定的幅度范围内和一定时区内变化的灰色量，并把随机过程看成灰色过程。

现有的问题：（小样本事件）
由于受到噪声的干扰，需要采用统计的方法研究给定的某一数据序列。但是统计的方法要求数据量非常大，并且计算量大，也无法对动态数据的发展趋势进行预测，尤其是小样本数据，统计方法更显得力不从心。

灰色序列的好处：
灰色系统认为：尽管客观系统表象复杂、数据离乱，但它总是有整体功能的，因而必然蕴含某种内在规律，关键在于如何选择适当的方式去挖掘它和利用它。一切灰色序列都能通过某种生成弱化其随机性，显现其规律性。

方法论：
设 $X = [x (1), x (2), ..., x (n)]$ 为原始序列， $D$ 为作用于 $X$ 的算子， $X$ 经过算子 $D$ 的作用后得到： $X D = [x (1) d, x (2) d, ..., x (n) d]$ 。称D为序列算子，称XD为一阶算子作用序列。
序列算子可以作用多次，相应得到的序列成为二阶序列、三阶序列，… …，相应的算子称为一阶算子，二阶序列算子… …

(1) 均值生成算子

使用场景：
在搜集数据时，常常由于一些不易克服的困难导致数据序列出现空缺（即空穴）；而有些数据序列虽然完整，但由于系统行为在某个时点上发生突变而形成异常数据，剔除异常数据后就会留下空穴。如何填补序列空穴自然成为数据处理过程中首先遇到的问题。均值生成时常用的构造新数据，填补原序列空穴、生成新序列的方法。

方法论：
设序列在 $k$ 处出现空缺，记为 $\varnothing(k)$ ，即
$X=[x(1),x(2),...,x(t-1),\varnothing(t),x(t+1),...,x(n)]$ 称 $x (t - 1)$ 和 $x (t + 1)$ 为 $\varnothing(t)$ 的界值，前者为前界，后者为后界。
当 $\varnothing(t)$ 是由 $x (t - 1)$ 和 $x (t + 1)$ 生成时，称生成值 $x (t)$ 为 $[x (t - 1), x (t + 1)]$ 的内点，而 $\varnothing(t)=x^*(t)=0.5x(t-1)+0.5x(t+1)$ 称为近邻均值生成数。由近邻均值生成数构成的序列 $Z$ 就称为近邻均值生成序列，记为 $Z = ME A N (X)$ 。
$Z = [z (1), z (2), ..., z (n)]$ 式中， $z (t) = 0.5 x (t - 1) + 0.5 x (t + 1)$ .

(2) 累加生成算子

适用场景：
累加生成可以看出灰量积累过程的发展趋势，使杂乱的原始数据中蕴含的积分特性或规律充分表现出来。

方法论：
设 $X^0=[x^0(1),x^0(2),...,x^0(n)]$ 为原始序列， $D$ 为序列算子，即
$X^0D=[x^0(1)d,x^0(2)d,...,x^0(n)d]$ 式中，
$x^0(t)=\sum_{i=1}^{t}x^0(t)\quad(t=1,2,3,...,n)$
则称 $D$ 为 $X^0$ 的一次累加算子，记为1-AGO。同样，可以有二阶、三阶、 $r$ 阶的累加生成算子，可以记为
$x^r(t)d=\sum_{i=1}^tx^{r-1}(i)\quad (t=1,2,3,...,n)$
由累加生成算子生成的序列称为累加生成数。如果原始序列为非负准光滑序列，则其一次累加生成序列具有准指数性质。原始序列越光滑，生成后指数规律越明显。

(3) 累减生成算子

方法论：
设 $X^0=[x^0(1),x^0(2),...,x^0(n)]$ 为原始序列， $D$ 为序列算子，即
$X^0D=[x^0(1)d,x^0(2)d,...,x^0(n)d]$ 式中，
$x^0(t)=x^0(t)-x^0(t-1)\quad(t=1,2,3,...,n)\quad x^{(1)}(0)=0$
则称 $D$ 为 $X^0$ 的一次累减算子，记为1-IAGO。同样，可以有二阶、三阶、 $r$ 阶的累减生成算子。
由累减生成算子生成的序列称为累减生成数。

(4) 效果测度

效果测度就是对于局势所产生的实际效果，在不同的目标之间进行比较的量度。在实际中，所采用的效果往往依据目标的效果而定。

i) 序列极性的有关符号

$\rho_{ol(max)}$ 表示极大值极性，即样本值越大越接近目标。
$\rho_{ol(min)}$ 表示极小值极性，即样本值越小越接近目标。
$\rho_{ol(men)}$ 表示适中值极性，即只有样本值适中才接近目标。

ii) 效果测度的符号

UEM：上限效果测度，表示极大值极性的效果测度。
LEM：下限效果测度，表示极小值极性的效果测度。
MEM：适中效果测度，表示适中值极性的效果测度。

iii) 效果测度的计算公式

UEM：
$r^0(k)=\frac{x^0(k)}{\max_k\{x^{(0)}(k)\}}$
LEM：
$r^0(k)=\frac{\min_k\{x^{(0)}(k)\}}{x^0(k)}$
MEM：
$r^0(k)=\frac{\min_k\{x^{(0)}(k),x^0(0)\}}{\max_k\{x^{(0)}(k),x^0(0)\}}$ 式中： $x (0)$ 表示适中值。

二、灰色分析

2.1 灰色关联分析

适用场景：
在实际系统中，其性能指标常常取决于多个因素。人们常常希望知道众多因素中，哪些是主要因素，哪些是次要因素，哪些因素对系统发展强大。哪些因素对系统发展影响小，哪些因素对系统发展起推动作用需要加强，哪些因素对系统发展起阻碍作用需要抑制，等等。

主要目的：
关联分析的主要目的就是从众多的系统影响因素中找到对性能指标影响比较大的因素，从而为进一步的决策服务。

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度越大；反之就越小。在客观世界中，有许多因素之间的关系是灰色的，分不清哪些因素关系密切，哪些因素关系不密切，这样就很难找到主要矛盾和主要特性。灰因素关联分析，目的是定量地表述诸多因素之间的关联程度，从而揭示灰色系统的主要特性。关联分析是灰色系统分析和预测的基础。

方法论：
选取参考数列 $x_0=\{x_0(t)|t=1,2,...,n\}$ ，假设有 $m$ 个比较数列 $x_i=\{x_i(t)|t=1,2,...,n\},i=1,2,...,m$ 则称 $\zeta_i(t)=\frac{mm+\rho\cdot MM}{|x_0(t)-x_i(t)|+\rho\cdot MM}$ 为比较数列 $x_i$ 对参考数列 $x_0$ 在 $t$ 时刻的关联系数，其中 $mm=\min_i\min_t|x_0(t)-x_i(t)|$ 称为两级最小差， $MM=\max_i\max_t|x_0(t)-x_i(t)|$ 称为两级最大差， $\rho\in[0,+\infty)$ 为分辨系数。一般而言， $\rho\in[0,1]$ ， $\rho$ 越大，分辨率越高；反之亦然。
上式定义的关联系统由于是不同时刻的关联系数，为了比较两个数列的关联关系，需要综合考虑各个时刻的关联系数，为此定义 $r_i=\frac1n\sum_{t=1}^n\zeta_i(t)$ 为数列 $x_i$ 和数列 $x_0$ 之间的关联度（绝对关联度。
(注意《预测理论与方法及其MATLAB实现》一书中对关联度定义的公式有误)

从定义中可以看出，两个数列之间的关联度是不同时刻关联关系的综合，将分散的信息集中处理。利用关联度的概念可以进行各种问题的因素分析，找出影响性能指标的关键因素，也可能对各个因素的重要程度进行排序。

2.2 无量纲化关键算子

在做关联度分析时，由于不同的数列采用不同的量纲，数量级上可能差别很大，因此首先要将不同的数列无量纲化，同时还需要区分两个数列之间的相关是正相关还是负相关。但是根据关联度的定义，无法看出这种情况，下面几个关键算子正式为了解决上述问题而提出的。

初值化算子

设 $X_i=[x_i(1),x_i(2),...,x_i(n)]$ ， $D_1$ 为序列算子，即
$X_iD_1=[x_i(1)d_1,x_i(2)d_1,...,x_i(n)d_1]$ 式中
$x_i(t)d_1=\frac{x_i(t)}{x_i(1)},\quad x_i(1)\neq0\quad (t=1,2,...,n)$ 则称 $D_1$ 为初始化算子， $X_iD_1$ 为初始化算子 $D_1$ 的象，简称初值象。

均值化算子

设 $X_i=[x_i(1),x_i(2),...,x_i(n)]$ ， $D_2$ 为序列算子，即
$X_iD_2=[x_i(1)d_2,x_i(2)d_2,...,x_i(n)d_2]$ 式中
$x_i(t)d_2=\frac{x_i(t)}{\sum_{t=1}^nx_i(t)},\quad (t=1,2,...,n)$ 则称 $D_2$ 为均值化算子， $X_iD_2$ 为均值化算子 $D_2$ 的象，简称均值象。

区间化算子

设 $X_i=[x_i(1),x_i(2),...,x_i(n)]$ ， $D_3$ 为序列算子，即
$X_iD_3=[x_i(1)d_3,x_i(2)d_3,...,x_i(n)d_3]$ 式中
$x_i(t)d_3=\frac{x_i(t)-\min_tx_i(t)}{\max_tx_i(t)-\min_tx_i(t)},\quad (t=1,2,...,n)$ 则称 $D_3$ 为区间化算子， $X_iD_3$ 为区间化算子 $D_3$ 的象，简称区间值象。

逆化算子

设 $X_i=[x_i(1),x_i(2),...,x_i(n)]$ ， $D_4$ 为序列算子，即
$X_iD_4=[x_i(1)d_4,x_i(2)d_4,...,x_i(n)d_4]$ 式中
$x_i(t)d_4=1-{x_i(t)},\quad (t=1,2,...,n)$ 则称 $D_4$ 为逆化算子， $X_iD_4$ 为逆化算子 $D_4$ 的象，简称逆化象。

倒数化算子

设 $X_i=[x_i(1),x_i(2),...,x_i(n)]$ ， $D_5$ 为序列算子，即
$X_iD_5=[x_i(1)d_5,x_i(2)d_5,...,x_i(n)d_5]$ 式中
$x_i(t)d_5=\frac1{x_i(t)},\quad x_i(t)\neq0\quad (t=1,2,...,n)$ 则称 $D_1$ 为倒数化算子， $X_iD_5$ 为初始化算子 $D_5$ 的象，简称倒数化象。

2.3 数据预处理

为了满足数据的标准化和线性化要求，可以将数据序列按下列三种情况分类预处理，这个步骤也可叫灰色关联生成。

(1) 期望值越大越好

$x^*(k)=\frac{x^{(0)}(k)-\min_kx^{(0)}(k)}{\max_kx^{(0)}(k)-\min_kx^{(0)}(k)},\quad (t=1,2,...,n)$

(2) 期望值越小越好

$x^*(k)=\frac{\max_kx^{(0)}(k)-x^{(0)}(k)}{\max_kx^{(0)}(k)-\min_kx^{(0)}(k)},\quad (t=1,2,...,n)$

(3) 期望值越接近目标越好

$x^*(k)=1-\frac{|x^{(0)}(k)-OB|}{\max\{\max_kx^{(0)}(k)-OB,OB-\max_kx^{(0)}(k)\}},\quad (t=1,2,...,n)$ 式中： $OB$ 为 $x^{(0)}(k)$ 的目标值。

2.4 关联分析的主要步骤

重要方法论！！！

根据评价目的确定评价指标值，搜集评价数据。
确定参考序列 $X_0$ 并进行预处理。参考序列应该是一个理想的比较标准，可以由各指标的最优值（或最劣值）构成，也可以根据评价的目的选择其他参照值。
对指标数列用关联算子进行无量纲化（也可以不进行无量纲化）。
逐个计算每个被评价对象指标序列与参考序列对应元素的绝对差值，即 $\Delta_i(t)=|x_0'(t)-x_i'(t)|(t=1,2,3,...,n;i=1,2,3,...,m)$ 。
确定 $mm=\min_i\min_t|x_0(t)-x_i(t)|$ 和 $MM=\max_i\max_t|x_0(t)-x_i(t)|$ 。
计算关联系数，即分别计算每个比较序列与参考序列对应元素的关联系数：
$r(x_0'(t),x_i'(t))=\frac{mm+\rho\cdot MM}{\Delta_i(t)+\rho\cdot MM}\quad (t=1,2,3,...,n)$
计算关联度：
$r(X_0,x_i)=\frac1n\sum_{t=1}^nr_{0i}(t)$
依据各观察对象的关联度，得出综合评价结果。

三、灰色系统建模

3.1 GM(1,1)模型

给定序列：
$X^0=[x^0(1)\quad x^0(2)\quad ... \quad x^0(n)]$ $X^1=[x^1(1)\quad x^1(2)\quad ... \quad x^1(n)]$ $Z^1=[z^1(1)\quad z^1(2)\quad ... \quad z^1(n)]$ 式中： $X^0$ 为原始序列； $X^1$ 为 $X^0$ 的1-AGO序列； $Z^1$ 为 $X^1$ 的近邻生成序列。则方程 $x^0(k)+a z^1(k)=b$ 为一元一阶微分方程，也称GM(1,1)模型。

设 $\hat{a}=(a,b)$ 为参数列，令
$Y=\begin{bmatrix} x^0(2) \\ x^0(3) \\ ... \\ x^0(n) \end{bmatrix}\quad B=\begin{bmatrix} -z^1(2) & 1\\ -z^1(3) & 1 \\ ...&... \\ -z^1(n) & 1 \end{bmatrix}$ 则灰色微分方程 $x^0(k)+az^1(k)=b$ 的最小二乘估计参数列满足：
$\hat{a}=(B^TB)^{-1}B^TY$ 称 $\frac{dx^{(1)}}{dt}+ax^{(1)}=b$ 为灰色微分方程的白化模型，也称影子方程，其解
$x^{(1)}(t+1)=(x^{(1)}(0)-\frac ba)e^{-at}+\frac ba\quad (t=0,1,2,3,...,n)$ 称为时间响应函数。
取 $x^{(1)}(0)=x^{(1)}(1)$ ，则
$\hat{x}^{(1)}(t+1)=(x^{(1)}(1)-\frac ba)e^{-at}+\frac ba\quad (t=0,1,2,3,...,n)$ 可以得到原始序列的预测序列：
$\hat{x}^{(0)}(t)=\hat{x}^{(1)}(t)-\hat{x}^{(1)}(t-1)=(x^{(0)}(1)-\frac ba)(1-e^a)e^{-a(t-1)}\quad (t>1)$

GM(1,1)模型由于自身的优点使其被广泛应用于数据不全面，信息不确定的领域进行预测研究，可以得到较高的预测精度，但也有很多情况是GM(1,1)模型不能预测的。一般当 $∣ a ∣ < 2$ 时，GM(1,1)有意义；但随着 $a$ 的取值不同，预测效果也不同。通过大量的实际问题验证，可以得出GM(1,1)的使用条件：

(1) 当 $-a\le0.3$ 时。可用于中长期的预测；
(2) 当 $0.3\lt-a\le0.5$ 时。可用于短期预测，中长期预测慎用；
(3) 当 $0.5\lt-a\le0.8$ 时。作短期预测应十分谨慎；
(4) 当 $0.8\lt-a\le1$ 时。应采用残差修正GM(1,1)模型；
(5) 当 $-a\ge1$ 时。不宜采用GM(1,1)模型

一般来说，当 $a$ 的取值满足 $a\in(\frac{-2}{n+1},\frac2{n+1})$ ，且级比 $\sigma^{(0)}=\frac{x^{(0)}(t-1)}{x^{(0)}(t)}(t\ge2)$ 取值满足 $\sigma^{(0)}\in(e^{\frac{-2}{n+1}},e^{\frac2{n+1}})$ 时，所建模型GM(1,1)才可行有效，可以获得较高的精度。

3.2 GM(1,1)模型检验

模型建立以后，应先对模型精度进行检验，模型精度检验合格后方可用于预测。
GM(1,1)模型的检验有残差检验、关联度检验和后验差检验。

(1) 残差检验

概念：
残差检验是对模型值与实际值的残差进行逐点检验。

方法论：
绝对残差序列
$\Delta^{(0)}=\{\Delta^{(0)}(i),i=1,2,3,...,n\},\quad \Delta^{(0)}(i)=|x^{(0)}(i)-\hat{x}^{(0)}(i)|×100\%$ (注意《预测理论与方法及其MATLAB实现》一书中对绝对残差的定义的公式有误)

相对残差序列
$\varphi=\{\varphi_i,i=1,2,3,...,n\},\quad \varphi_i=|\frac{\Delta^{(0)}(i)}{x^{(0)}(i)}|×100\%$ 计算平均相对误差
$\bar{\varphi}= \frac{1}{n} \sum_{i=1}^n \varphi_i$
用平均相对误差判定模型的适用性（见下表6.1），若 $\bar{\varphi}\lt20\%$ 成立，则称模型为残差检验合格模型。如果残差太大使得 $\bar{\varphi}\gt20\%$ 成立，则必须修正模型使之满足精度要求后，才可以进行预测。
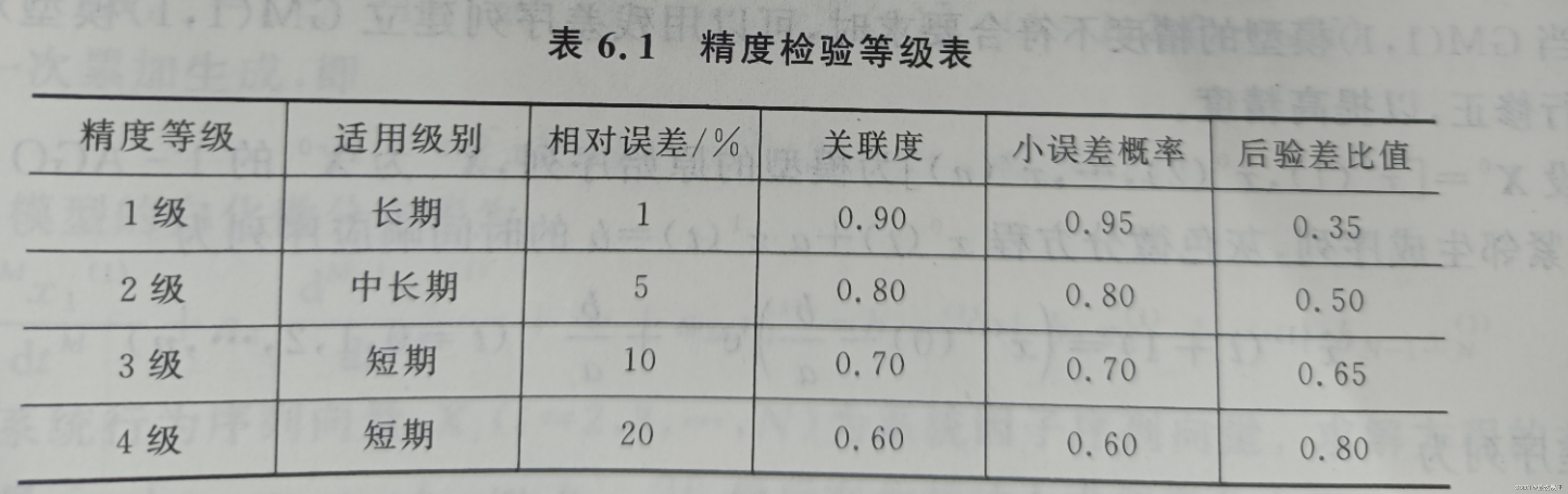
在这里插入图片描述

(2) 关联度检验

关联度检验是通过考察模型值曲线和建模序列曲线的相似程度来进行检验。按阡陌所述的关联度计算方法，计算出 $\hat{x}^{(0)}(i)$ 与原始数列 $x^{(0)}(i)$ 的关联系数，然后计算出关联度，对照表6.1判断关联度是否大于0.6的检验标准。根据检验，若满足此检验标准，称为关联度合格模型。关联度越大，说明模型拟合得越好。

(3) 后验差检验

概念：
后验差检验是对残差分布的统计特性进行检验。

方法论：

计算原始数列的平均值
$\bar{x}^{(0)}=\frac1n\sum_{i=1}^nx^{(0)}(i)$
计算原始数列的均方差
$S_1=[\frac{\sum_{i=1}^n(x^{(0)}(i)-\bar{x}^{(0)})^2}{n-1}]^{\frac12}$
计算残差的均值
$\bar{\Delta}=\frac1n\sum_{i=1}^n\Delta^{(0)}(i)$
计算残差的方差
$S_2=[\frac{\sum_{i=1}^n(\Delta^{(0)}(i)-\bar{\Delta})^2}{n-1}]^{\frac12}$
计算方差比
$C=S_1/S_2$
计算小残差概率
$P=P\{|\Delta^{(0)}(i)-\bar{\Delta}|\lt0.6745S_1\}$
令 $S_0=0.6745S_1,e=|\Delta^{(0)}(i)-\bar{\Delta}|$ ，即 $P=P\{e_i\lt S_0\}$ .

对于给定的 $C_0\gt0$ ，当 $C\lt C_0$ 时，称模型为均方差比合格模型。对于给定的 $P_0\gt 0$ ，当 $P\lt P_0$ 时，称模型为小残差概率合格模型。
若对残差检验、关联度检验、后验差检验在允许的范围内，则可以用所建立的模型进行预测；否则应进行残差修正。

3.3 GM(1,1)残差修正

现有的问题：
GM(1,1)模型精度不符合要求，不通过检验。

方法论：
给定序列：
$X^0=[x^0(1)\quad x^0(2)\quad ... \quad x^0(n)]$ 为原始序列； $X^1$ 为 $X^0$ 的1-AGO序列； $Z^1$ 为 $X^1$ 的近邻生成序列，灰色微分方程 $x^0(k)+a z^1(k)=b$ 的时间响应序列为
$\hat{x}^{(0)}(t+1)=(x^{(0)}(1)-\frac ba)(1-e^a)e^{-at}\quad (t=0,1,...,n)$ 其残差序列为
$\epsilon^{(0)}=\{\epsilon^{(0)}(1),\epsilon^{(0)}(2),...,\epsilon^{(0)}(n)\}$ 式中： $\epsilon^{(0)}(t)=x^{(1)}(t)-\bar{x}^{(1)}(t)$ ，若存在 $t_0$ ，满足：

对任意的 $t\ge t_0$ ， $\epsilon^{(0)}(t)$ 的符号一致；
$n-t_0\ge4$ ，则称
$(|\epsilon^{(0)}(t_0)|,|\epsilon^{(0)}(t_0+1)|,...,|\epsilon^{(0)}(n)|)$
为可建模残差尾段，仍记为 $\epsilon^{(0)}=\{\epsilon^{(0)}(1),\epsilon^{(0)}(2),...,\epsilon^{(0)}(n)\}$ 对于可建模残差尾段，其1-AGO序列 $\{\epsilon^{(1)}(k_0),\epsilon^{(1)}(k_0+1),...,\epsilon^{(1)}(n)\}$ 的GM(1,1)时间响应序列为

$\hat{\epsilon}^{(1)}(t)=(\epsilon^{(0)}(t_0)-\frac {b_\epsilon}{a_\epsilon})e^{-a(t-t_0)}+\frac {b_\epsilon}{a_\epsilon} \quad (t\ge t_0)$ 最后还原得残差尾段的估计序列为 $\hat{\epsilon}^{(0)}=\{\hat{\epsilon}^{(0)}(t_0),\hat{\epsilon}^{(0)}(t_0+1),...,\hat{\epsilon}^{(0)}(n)\}$ 式中
$\hat{\epsilon}^{(0)}(t)=-a_{\epsilon}(\epsilon^{(0)}(t_0)-\frac {b_\epsilon}{a_\epsilon})e^{-a(t-t_0)} \quad (t\ge t_0)$
因为残差尾段从残差数列的第 $t_0$ 个数据开始取，所以，当 $t\lt t_0$ 时， $\hat{x}^{(0)}(t)$ 所对应的残差修正值为0。考虑到公式的通用性和完整性，可在 $\hat{\epsilon}^{(0)}(t)$ 前配一个系数，所以有
$\hat{x}_\epsilon^{(0)}(t)=\hat{x}^{(0)}(t)\pm\eta(t)\hat{\epsilon}^{(0)}(t)\\ \eta(t)=\begin{cases} 0 &t\lt t_0 \\1 &t\ge t_0 \end{cases}$
若用 $\hat{\epsilon}^{(0)}(k)$ 修正 $\hat{X}^{(1)}$ ，则称修正后的时间响应式
$\hat{x}^{(0)}(t+1)=\begin{cases} (x^{(0)}-\frac ba)e^{-at}+\frac ba &t\lt t_0 \\ [(x^{(0)}-\frac ba)e^{-at}+\frac ba]\pm a_\epsilon(\epsilon^{(0)}(t_0)-\frac{b_\epsilon}{a_\epsilon})e^{-a_\epsilon(t-t_0)} &t\ge t_0 \end{cases}$ 为残差修正GM(1,1)模型。

【注】由于以下的GM模型都是在GM(1,1)的基础上改写灰色微分方程得到的，为了减少文章的冗余性，简单阐述其适用场景和修改方式即可。

3.4 GM(M,N)模型

适用场景：
GM(1,1)模型适用于具有系数规律变化的序列，只能描述单调变化过程。对于非单调的摆动发展序列，要反映描述对象的长期、连续、动态特性，就要建立GM(M,N)模型。模型中的M表示方差的阶数，N表示变量的个数。

修改方式：
将GM(1,1)的灰色微分方程改为多元高阶的白化微分方程，通过OLS求得系数向量即可。

3.5 GM(1,N)模型

修改方式：
将GM(M,N)的模型的M取值为1。

3.6 GM(0,N)模型

适用场景：
GM(0,N)不含导数项，亦称为静态模型。模型形如多元线性回归模型，但有着本质的区别，多元线性回归是基于原始数列的，而这个模型是基于一次累加生成序列的，通过累加生成有效的消除了序列的波动性。

修改方式：
将GM(M,N)的模型的M取值为0。

3.7 灰色Verhulst模型

灰色Verhulst模型也称为有限增长灰模型（或S模型）。它主要针对的是当系统受到外界环境的制约时，有一个高速增长之后转为平缓增长的近似型增长趋势。
Verhulst模型为
$x^{(0)}+az^{(1)}=b(z^{(1)})^2$
其白化方程为
$\frac{dx_1^{(1)}}{dt}+ax^{(1)}=b(x^{(1)})^2$ 式中： $b(x^{(1)})^2$ 称为竞争项，解为：
$x^{(0)}(t)=\frac{ax^{(1)}(0)}{bx^{(1)}(0)+[a-x^{(1)}(0)]e^{at}}$ $x^{(1)}_1(0)$ 取为 $x^{(1)}_1(0)$ ，可得灰色Verhulst模型的时间响应式：
$\hat{x}^{(0)}(t+1)=\frac{ax^{(0)}(1)}{bx^{(0)}(1)+[a-x^{(0)}(1)]e^{at}}$ 有待辨识的参数向量 $\hat{a}=[a,b]^T$ ，解得
$\hat{a}=(B^TB)^{-1}B^TY$ 式中
$B=\begin{bmatrix} -\frac12[x^{(1)}(1)+x^{(1)}(2)] & -\frac14[x^{(1)}(1)+x^{(1)}(2)]^2 \\ -\frac12[x^{(1)}(2)+x^{(1)}(3)] & -\frac14[x^{(1)}(2)+x^{(1)}(3)]^2 \\ ... & ... \\ -\frac12[x^{(1)}(n-1)+x^{(1)}(n)] & -\frac14[x^{(1)}(n-1)+x^{(1)}(n)]^2 \\ \end{bmatrix}$

$Y=[x^{(0)}(2)\quad x^{(0)}(3)\quad ...\quad x^{(0)}(n)]^T$

灰色GM(1,1)模型适用于具有较强指数规律的模型，而灰色Verhulst模型则适用于非单调的摆动发展序列，或者具有饱和状态的S形序列，而且当 $a\lt 0,t\to \infty,e^{at}\to 0,x^{(1)}(t)\to a/b$ 时，表明此时的 $x^{(t)}\approx0$ 系统已经趋于稳定。

相关还有GM(1,1)幂模型、灰色灾变预测模型等。
其中，幂模型是对灰色Verhulst模型做了进一步推广，将一次幂推广成 $a$ 次幂的背景值，仍然为一元一次微分方程的形式，所以可记作为GM(1,1)模型。灰色灾变模型的任务是给出下一个或几个异常值出现的时刻，一遍人们提前准备，采取对策，减少损失。处理对象为原始序列的灾变子序列（上灾变序列和下灾变序列）和灾变时间序列。

四、模型的改进

这一部分总结比较草率，主要概括了一下可以去优化改进的方向，针对模型的话就题论题时最好的，所以这里不过多展开【其实是码累了…】。

4.1 基于残差修正的改进模型

见GM(1,1)残差修正。

4.2 基于初始条件和信息更新的改进模型

1. 新初值GM模型（GMn模型）

2. 部分信息模型、灰色新信息模型和新陈代谢模型

(1) 部分信息GM模型

(2) 灰色新信息模型和新陈代谢模型

4.3 基于数据变换的改进模型

1. 加入序列算子的GM模型

2. 加入权重系数的模型

3. 离散GM(1,1)模型

4. 灰色非等时距序列模型

4.4 针对内部建模机制的改进模型

1. 灰色模型的极差格式

2. 灰色Gompertz模型

3. 灰色Logistic模型

四、实战模拟

这里简单实现GM(1,1)模型的函数。

function []=greymodel(y)
% 本程序主要用来计算根据灰色理论建立的模型的预测值。
% 应用的数学模型是 GM(1,1)。
% 原始数据的处理方法是一次累加法。
y=input('请输入数据 ');
n=length(y);
yy=ones(n,1);
yy(1)=y(1);
for i=2:n
    yy(i)=yy(i-1)+y(i);
end
B=ones(n-1,2);
for i=1:(n-1)
    B(i,1)=-(yy(i)+yy(i+1))/2;
    B(i,2)=1;
end
BT=B';
for j=1:n-1
    YN(j)=y(j+1);
end
YN=YN';
A=inv(BT*B)*BT*YN;
a=A(1);
u=A(2);
t=u/a;
i=1:n+2;
yys(i+1)=(y(1)-t).*exp(-a.*i)+t;
yys(1)=y(1);
for j=n+2:-1:2
    ys(j)=yys(j)-yys(j-1);
end
x=1:n;
xs=2:n+2;
yn=ys(2:n+2);
plot(x,y,'^r',xs,yn,'*-b');
det=0;

sum1=0;
sumpe=0;
for i=1:n
    sumpe=sumpe+y(i);
end
pe=sumpe/n;
for i=1:n;
    sum1=sum1+(y(i)-pe).^2;
end
s1=sqrt(sum1/n);
sumce=0;
for i=2:n
    sumce=sumce+(y(i)-yn(i));
end
ce=sumce/(n-1);
sum2=0;
for i=2:n;
    sum2=sum2+(y(i)-yn(i)-ce).^2;
end
s2=sqrt(sum2/(n-1));
c=(s2)/(s1);
disp(['后验差比值为：',num2str(c)]);
if c<0.35
    disp('系统预测精度好')
else if c<0.5
        disp('系统预测精度合格')
    else if c<0.65
            disp('系统预测精度勉强')
        else
            disp('系统预测精度不合格')
        end
    end
end
            
disp(['下个拟合值为 ',num2str(ys(n+1))]);
disp(['再下个拟合值为',num2str(ys(n+2))]);

参考资源

[1] 《预测理论与方法及其MATLAB实现》许国根，贾瑛，黄智勇，沈可可
[2] 《数学建模算法与应用（第三版）》司守奎，孙玺菁
[3] 【数学建模】灰色预测模型（预测）博主：Edward-Phoenix
[4] 灰色预测博主：Mangoit
[5] 灰色预测，看这一篇就够了知乎博主：阳寜

总结（一些很久没更的唠嗑）

距离国赛仅剩18天，抓紧复习一下重点模型吧！

首先，为博客写得越来越少找个借口。虽然blog更得越来慢，但收藏夹的东西越来越多了。可能觉得能力实在渺小，我等渣渣还需要大量的沉淀和知识的输入，知识的整理与输出就显得比较落后了。等到踏实下来，学了些东西后会努力“双向”发展的！
然后，浅聊一下自己这两天模拟的心得。yysy，for me，模拟赛就是个坑，因为每次模拟赛都是以“寄”告终的（去年是，今年也是）。去年选的是“妈妈杯”的大数据题，数据处理起来难度很大。今年则是选择的是2022年深圳杯作为模拟演练的，时间是2天，事实证明，正如某乎上说的：不论是建模小白还是建模烙饼而言，深圳杯都算得上最难的数学建模赛事。模拟时间两天确实不合理，模拟难度与国赛出入较大，学科方向和算法侧重点也有一些差距，所以综合考虑下，打算暂停模拟练习。身为建模和代码手的我着实也被搞得心态有些焦灼。
经过了两天的简单讨论，及时发现了一些我们队伍存在的问题，好就好在，国赛前还有一些改进的时间，所以这两天也还不算亏。只能说壮士仍需加油！！！
最后，这几天会就重点的数学模型进行总结，按照我自己的总结方式——“使用场景+方法论+优劣”。希望最后半个月不负国赛，也希望数模大佬在评论区或私信批评指正！

【数据结构】图的深度优先遍历