并查集的简单实现

1、并查集的原理

并查集主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

1. 合并（Union）：把两个不相交的集合合并为一个集合
2. 查询（Find）：查询两个元素是否在同一个集合中

当然，这样的定义未免太过学术化，看完后恐怕不太能理解它具体有什么用。所以我们先来看看并查集最直接的一个应用场景：亲戚问题

描述(Description)

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。
规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。

输入(Input)

第一行:三个整数n,m,p，(n< =5000,m< =5000,p< =5000)，分别表示有n个人，m个亲戚关系，询问p对亲戚关系。 以下m行:每行两个数Mi，Mj，1< =Mi，Mj< =N，表示Mi和Mj具有亲戚关系。 接下来p行:每行两个数Pi，Pj，询问Pi和Pj是否具有亲戚关系

输出(Output)

P行，每行一个’Yes’或’No’。表示第i个询问的答案为"具有"或"不具有"亲戚关系。

初步分析觉得本题是一个图论中判断两个点是否在同一个连通子图中的问题。我们可以建立模型，把所有人划分到若干个不相交的集合中，每个集合里的人彼此是亲戚。为了判断两个人是否为亲戚，只需看它们是否属于同一个集合即可。因此，这里就可以考虑用并查集进行维护了。

2、并查集的引入

并查集的重要思想在于，用集合中的一个元素代表集合。我曾看过一个有趣的比喻，把集合比喻成帮派，而代表元素则是帮主。接下来我们利用这个比喻，看看并查集是如何运作的。

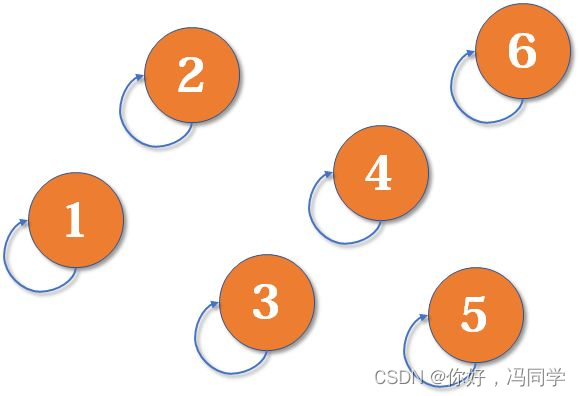
最开始，所有大侠各自为战。他们各自的帮主自然就是自己。（对于只有一个元素的集合，代表元素自然是唯一的那个元素）

现在1号和3号比武，假设1号赢了（这里具体谁赢暂时不重要），那么3号就认1号作帮主（合并1号和3号所在的集合，1号为代表元素）

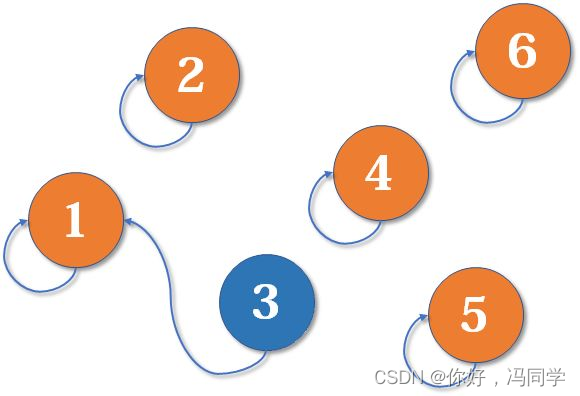
现在2号想和3号比武（合并3号和2号所在的集合），但3号表示，别跟我打，让我帮主来收拾你（合并代表元素）。不妨设这次又是1号赢了，那么2号也认1号做帮主。

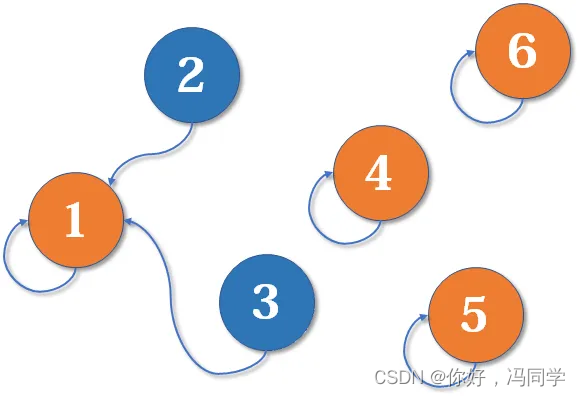
现在我们假设4、5、6号也进行了一番帮派合并，江湖局势变成下面这样：

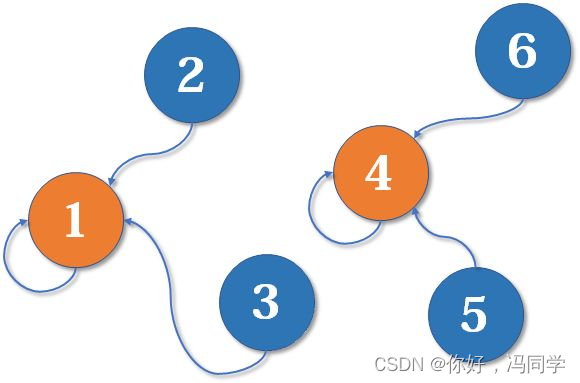
现在假设2号想与6号比，跟刚刚说的一样，喊帮主1号和4号出来打一架（帮主真辛苦啊）。1号胜利后，4号认1号为帮主，当然他的手下也都是跟着投降了。

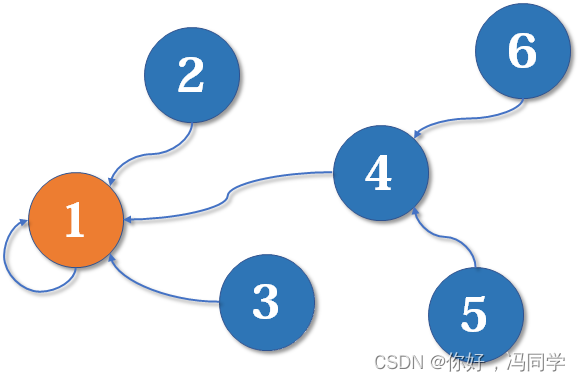
好了，比喻结束了。如果你有一点图论基础，相信你已经觉察到，这是一个树状的结构，要寻找集合的代表元素，只需要一层一层往上访问父节点（图中箭头所指的圆），直达树的根节点（图中橙色的圆）即可。根节点的父节点是它自己。我们可以直接把它画成一棵树：

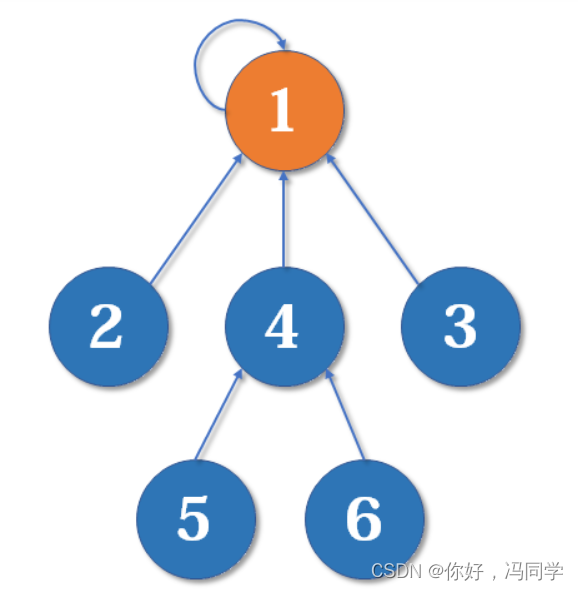
用这种方法，我们可以写出最简单版本的并查集代码。

3、路径压缩

最简单的并查集效率是比较低的。例如，来看下面这个场景：

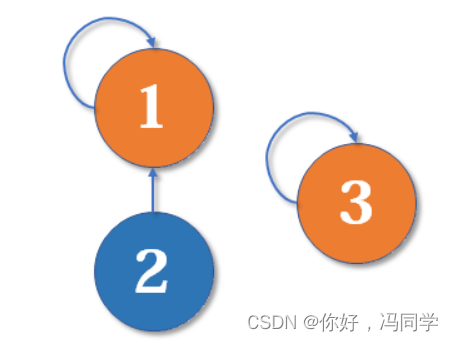
现在我们要merge(2,3)，于是从2找到1，fa[1]=3，于是变成了这样：

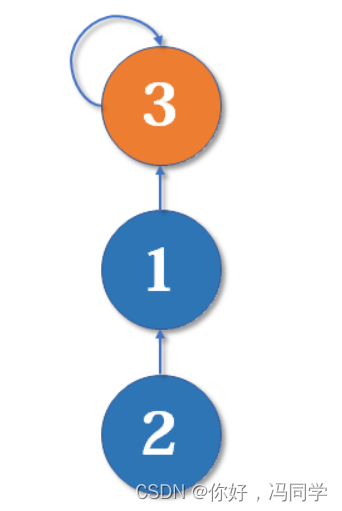
然后我们又找来一个元素4，并需要执行merge(2,4)：

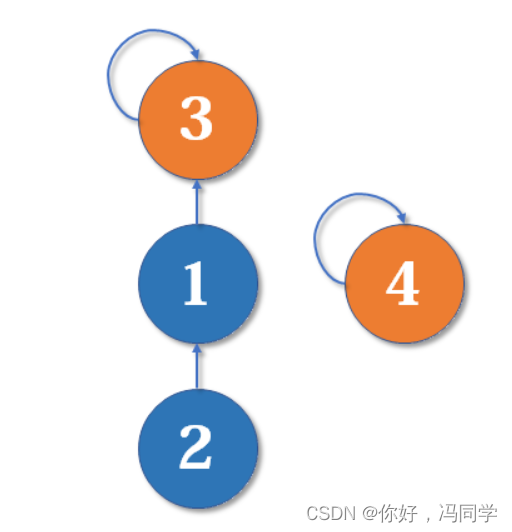
从2找到1，再找到3，然后fa[3]=4，于是变成了这样：

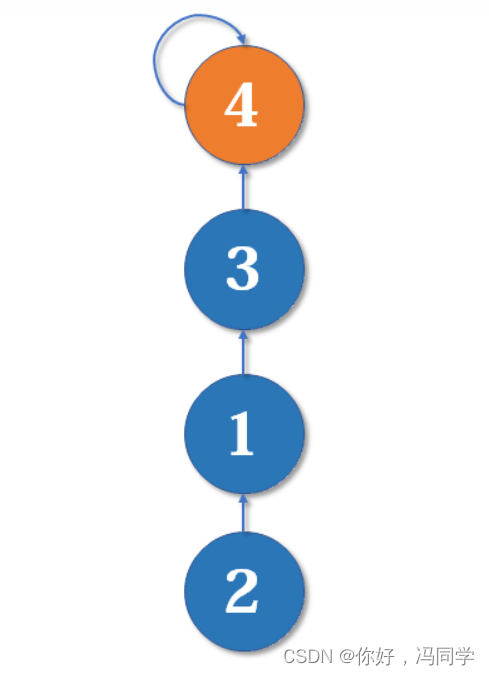
大家应该有感觉了，这样可能会形成一条长长的链，随着链越来越长，我们想要从底部找到根节点会变得越来越难。

怎么解决呢？我们可以使用路径压缩的方法。既然我们只关心一个元素对应的根节点，那我们希望每个元素到根节点的路径尽可能短，最好只需要一步，像这样：

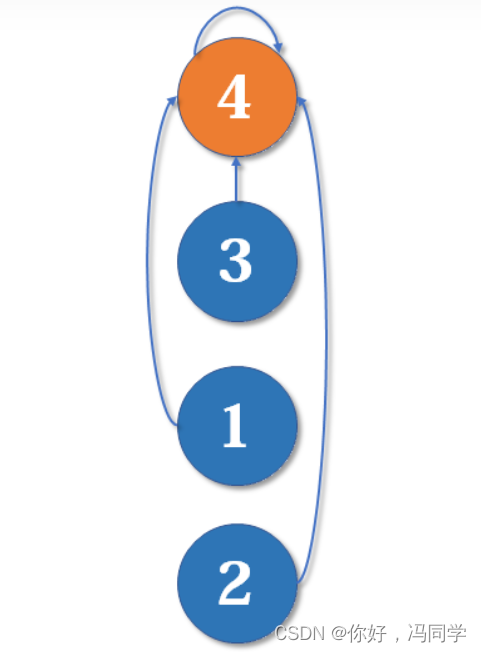
其实这说来也很好实现。只要我们在查询的过程中，把沿途的每个节点的父节点都设为根节点即可。下一次再查询时，我们就可以省很多事。

但其实，由于路径压缩只在查询时进行，也只压缩一条路径，所以并查集最终的结构仍然可能是比较复杂的。

例如，现在我们有一棵较复杂的树需要与一个单元素的集合合并：

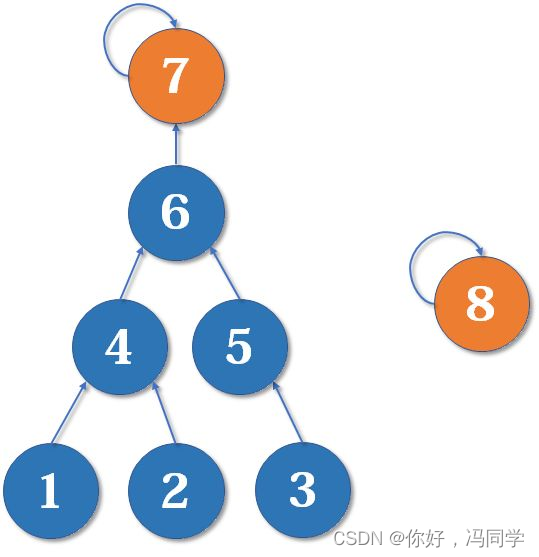
假如这时我们要merge(7,8)，如果我们可以选择的话，是把7的父节点设为8好，还是把8的父节点设为7好呢？

当然是后者。因为如果把7的父节点设为8，会使树的深度（树中最长链的长度）加深，原来的树中每个元素到根节点的距离都变长了，之后我们寻找根节点的路径也就会相应变长。虽然我们有路径压缩，但路径压缩也是会消耗时间的。而把8的父节点设为7，则不会有这个问题，因为它没有影响到不相关的节点。

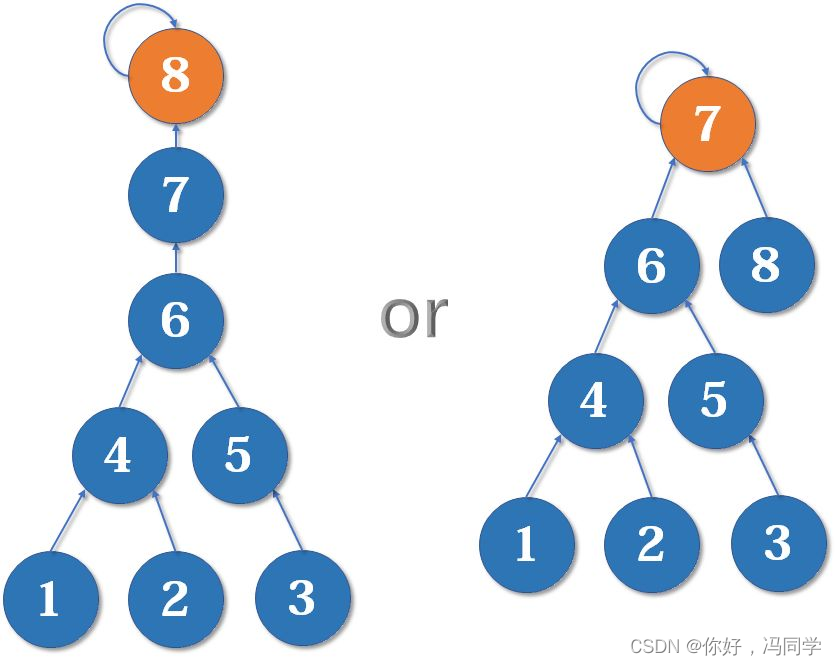
这启发我们：我们应该把简单的树往复杂的树上合并，而不是相反。因为这样合并后，到根节点距离变长的节点个数比较少。

4、整体实现

#pragma once
#include<vector>
#include<algorithm>
using namespace std;
class UnionFindSet
{
    
    
public:
	UnionFindSet(size_t n)
		:_ufs(n, -1)
	{
    
    }

	//合并
	void Union(int x1, int x2)
	{
    
    
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);

		//数据量小的集合往数据量大的集合合并
		//if (abs(_ufs[root1]) < abs(_ufs[root2]))
		//{
    
    
		//	swap(root1, root2);
		//}

		//如果root1和root2相等，说明在一个集合，就没必要进行合并了	
		if (root1 != root2)
		{
    
    
			//将root2合并到root1，root1集合的个数需要加上root2集合的个数
			_ufs[root1] += _ufs[root2];
			//将root1作为root2的根	
			_ufs[root2] = root1;
		}
	}

	//找根节点
	int FindRoot(int x)
	{
    
    
		int root = x;
		while (_ufs[root] >= 0)
		{
    
    
			root = _ufs[root];
		}

		//路径压缩
		//当前值到根路径上的所有值都进行压缩
		while (_ufs[x] >= 0)
		{
    
    
			//保存当前数值的父亲
			int parent = _ufs[x];
			_ufs[x] = root;
			x = parent;
		}
		return root;
	}
	
	bool Inset(int x1, int x2)
	{
    
    
		return FindRoot(x1) == FindRoot(x2);
	}

	//获取元素个数
	size_t SetSize()
	{
    
    
		int count = 0;
		for (size_t i = 0; i < _ufs.size(); ++i)
		{
    
    
			if (_ufs[i] < 0)
			{
    
    
				count++;
			}
		}
		return count;
	}
private:
	vector<int> _ufs;
};

参照：并查集